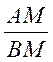Pré requis:

Point /ligne / plan : notions

ENVIRONNEMENT du dossier:

Index

Objectif précédent : Vocabulaire de base « le point »

Objectif suivant : Lieu géométriques; définition et classification

tableau 2°) Liste des cours sur le repérage

DOSSIER :

LIEUX GEOMETRIQUES ; Détermination (de la position ) d’un point :

·

	· A ) sur une ligne .
	· B ) sur un plan :
	- Coordonnées cartésiennes .
	- Les coordonnées bipolaires .
	- Coordonnées bi angulaires :
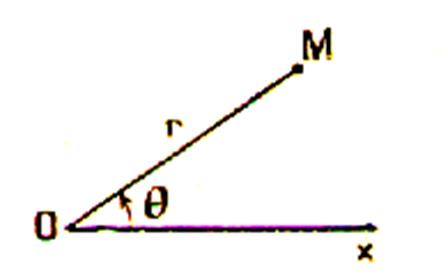
	- Coordonnées polaires .
	· C ) dans l’espace.
TEST	COURS	Devoir Contrôle	Devoir évaluation	Interdisciplinarité	Corrigé Contrôle	Corrigé évaluation

COURS

Détermination d’un point.

Point sur une ligne .

Sur une ligne donnée L se trouve un point M dont on veut préciser la position : il suffit pour cela de donner un nombre ( ce qui exprime qu’une figure en disant qu’une ligne est une figure à une dimension ) .

Ce nombre mesurera une certaine grandeur appelée « paramètre » , dont la connaissance fixera la position de « M » . Il est souhaitable qu’ à une valeur du paramètre corresponde un seul point « M » , et réciproquement.

Exemples :

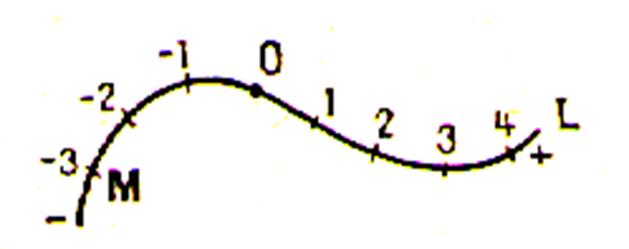
Sur la ligne L choisissons une origine O , des sens positifs et négatifs , une unité de longueur ; la position de tout point « M » sera caractérisée par son abscisse curviligne « x » = ( lire : mesure algébrique du bipoint OM )
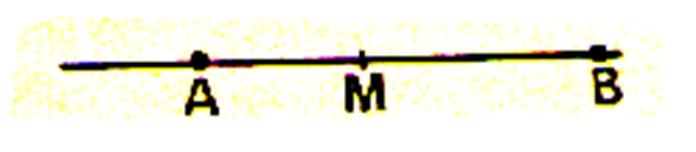
Ou bien encore , sur la ligne L choisissons deux points de repère A et B ; la position de tout point « M sera caractérisée par le rapport algébrique

Remarque :la détermination d’un point « M » par un nombre offre l’avantage de pouvoir introduire ce point « M » dans un calcul . (exemple problème de courriers) , ce que l’on ne pourrait pas faire si l’on se contentait d’une figure.

Point sur une surface .

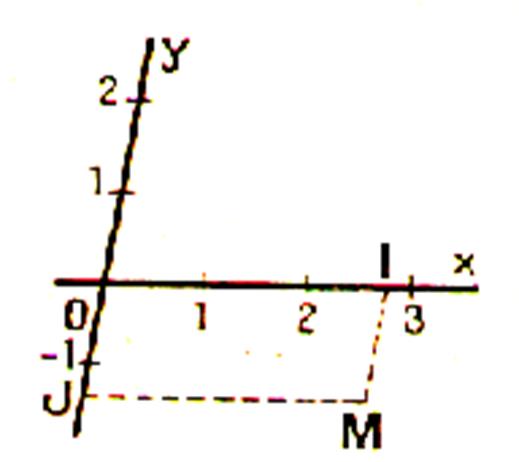
Sur une surface donnée « S » se trouve un point « M » dont on veut préciser la position : il faudra donner deux nombres (ce que l’on exprime en disant qu’une surface est une figure à deux dimensions ) . Ces nombres sont appelés « coordonnées *» de « M » .

*Il est souhaitable qu’à un système de coordonnées corresponde un seul point M et réciproquement .

Exemples de coordonnées ( on suppose que la surface S est un plan )

Coordonnées cartésiennes .
Choisissons deux axes x’Ox et y’Oy , orientés et gradués ; la position de tout point M est caractérisée par ses distances algébriques à ces deux axes : L’abscisse x = , l’ordonnée y = Le plus souvent on adopte des axes « rectangulaires ». Ce n’est pas indispensable. Quand les axes sont obliques , on préfère souvent compter les distances IM et JM parallèlement aux axes .
Ce système de coordonnées , inventés par Descartes ( 1596 –1650 ) est le plus parfait et le plus utile.(mais on peut en imaginer beaucoup d’autres .

Les coordonnées bipolaires .
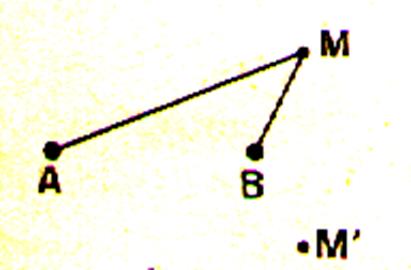
A et B étant deux points fixes , un point « M » est caractérisé par les distances AM et BM. Ce système n’est pas parfait , car deux points M et M’ symétriques par rapport à la droite AB ont les mêmes coordonnées. On l’utilise cependant assez souvent en géométrie.

Coordonnées bi angulaires :
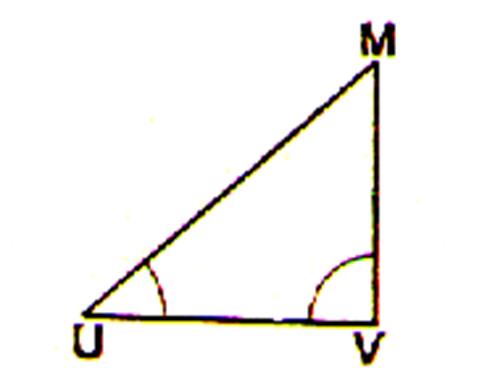
U et V étant deux points fixes , un point M est caractérisé par les angles à la base du triangle .Ce système employé en topographie , en artillerie …où la position d’un point visé M est caractérisée par deux angles appelés gisement ; on l’emploie en astronomie , et aussi pour certaines questions de géométrie .

Coordonnées polaires .

Une demi –droite Ox étant fixée , un point M est caractérisé par l’angle polaire xOM = q et la distance OM = r Par exemple, sur le plan de paris affiché à la porte d’une mairie , repérera une rue en tournant d’abord une manivelle d’un angle q , qui se mesure à l’aide d’un rapporteur formant le contour extérieur du plan ; puis , sur une manivelle même , la distance « r » est indiquée par une lettre de l’alphabet . Autre exemple plus savant : c’est par des coordonnées polaires qu’on précise la position de la terre , dans sa rotation autour du soleil . Si la surface S est une sphère (sphère terrestre ) , on caractérisera un point M par les coordonnées géographiques qui sont deux angles : longitude et latitude . De même pour la « sphère céleste »

Point dans l’espace

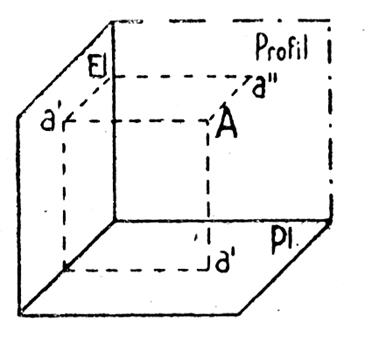
Pour déterminer la position d’un point « A » dans l’espace , il faudra trois nombres ( l’espace est à trois dimensions : « a ; a’  et a’’ » 

Il est possible d’imaginer quelques systèmes possibles , par généralisations des systèmes précédents.

TRAVAUX AUTO FORMATIFS.

CONTROLE:

Qu ‘appelle-t-on « paramètre »

Par quoi détermine –t-on la position d’un point ?

Citer les 4 principaux de coordonnées d’un point.

EVALUATION:

Représenter graphiquement les 4 types de coordonnées ( apporter quelques précisions)