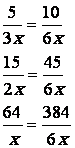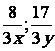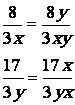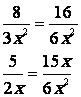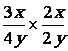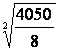Consigne :
TESTS D’ALGEBRE
N° 1
Ce test
contient 55 séries d'exercices ou problème types
|
Série: 1 |
|
Quel nom
donne t on à "x"; "y";…. ,que
représente - elle ? |
Inconnue
; elle représente une valeur numérique . |
|
SOS Cours |
|
|
Série: 2 |
Donner deux
exemples de valeur à "x" et
"y" pour chaque ensemble de
nombre
|
|
Soit "x" |
Soit "y" |
|
N |
3 ;
674 |
5;9 |
|
D |
6,21 ; 9,63 |
78,21;9,85 |
|
Z |
(-5) ;(+9) |
(+652) ;(-56789) |
|
D+ ou- |
(+3,00);(-65,8975) |
(+56,98521455) ; (-8,78) |
|
R |
(- |
(+7)/(-9) ; |
|
SOS Cours |
|
|
Série: 3 |
|
Soit les deux écritures |
Qu'indique la valeur numérique
"2" ? |
|
X2 |
Elle indique la
puissance de "x", ici ,au carrée , appelé
aussi : indice ou exposant . |
|
X2 |
Elle indique le deuxième
rang pris par la valeur de "x", elle porte le nom d'indice. |
|
SOS Cours |
|
TESTS D’ALGEBRE
N° 2
|
Série: 4 |
I )Calcul faisant intervenir des nombres entiers naturels.( addition)
|
Compléter les égalités suivantes :
|
Résoudre les équations suivantes |
Résultat |
|
Colonne 1 |
Colonne 2 |
Colonne 3 |
|
1
+… = 1 |
1+ x = 1 |
x = 0 |
|
1 + 1 =….. |
1+1 = x |
x = 2 |
|
5 + ….. = 8 |
5 + x = 8 |
x = 3 |
|
10 + ……= 17 |
10 + x = 17 |
x = 7 |
|
32 +…. .= 43 |
32 + x = 43 |
x = 11 |
|
136 + ……..= 237 |
136 + x = 237 |
x =101 |
|
359 + …… = 598 |
359 + x = 598 |
x =239 |
|
……. +
2384 = 6732 |
x. + 2384
= 6732 |
x =4348 |
|
Cas: 63 + …… =
56 |
Cas: 63 + x
= 56 |
x = (-7)voir les décimaux relatifs) |
|
SOS Cours |
|
|
Série: 5 |
II ) Calcul faisant intervenir des nombres entiers naturels (soustraction)
|
Compléter les opérations |
Résoudre |
Résultats |
|
Colonne 1 |
|
|
|
1-… =
1 |
1-
x = 1 |
x =0 |
|
1 - 1 =….. |
1-1 = x |
x =0 |
|
8
- ….. = 5 |
8 - x = 5 |
x = 3 |
|
17
- ……= 10 |
17 - x = 10 |
x =7 |
|
43 -…. .= 32 |
43 - x = 32 |
x = 11 |
|
237 - ……..= 136 |
237 - x = 136 |
x =101 |
|
598 - …… = 359 |
598 - x =
359 |
x =239 |
|
……. -
2384 = 6732 |
x - 2384
= 6732 |
x =4348 |
|
|
|
|
|
SOS Cours |
|
Série: 6 |
III ) calcul faisant intervenir des nombres entiers naturels (multiplication)
|
Compléter les opérations |
|
|
|
Colonne 1 (à compléter) |
Colonne 2 |
Colonne 3 |
|
1 |
1 |
x =1 |
|
1 |
1 |
x =1 |
|
8
|
8 |
x = 5 |
|
17
|
17 |
x =10 |
|
43 |
43 |
x = 4 |
|
237 |
237 |
x =7 |
|
598 |
598 |
x =13 |
|
……. |
x |
x =134 |
|
|
|
|
|
SOS Cours |
|
|
Série: 7 |
IV ) calcul faisant intervenir des nombres entiers naturels (division)
|
SOS Cours |
|
Compléter les opérations |
|
|
|
Colonne 1 (à compléter) |
Colonne 2 |
Colonne 3 |
|
1:… =
1 |
1: x
= 1 |
x =1 |
|
1 : 1 =….. |
1: 1 = x |
x =1 |
|
6 :……= 3 |
6 : x = 3 |
x=2 |
|
40
: ….. = 8 |
40 : x = 8 |
x = 5 |
|
170 :……=
17 |
170 : x = 17 |
x =10 |
|
172 :…. .= 43 |
172 : x = 43 |
x = 4 |
|
1659 :……..= 237 |
1659 : x = 237 |
x =7 |
|
7774 :…… = 598 |
7774: x =
598 |
x =13 |
|
319456 : ……
= 2384 |
319456: x = 2384 |
x =134 |
|
|
|
|
|
SOS Cours |
|
|
Série: 8 |
I )les Calculs font intervenir des
nombres décimaux non relatifs ( addition)
|
Compléter les opérations |
|
|
|
Colonne 1 |
Colonne 2 |
Colonne 3 |
|
0,1+… =
0,1 |
0,1+ x =0,1 |
x =0 |
|
0,1 + 0,1 =….. |
0,1+0,1 = x |
x =0,2 |
|
0,5 + ….. = 0,8 |
0,5 + x = 0,8 |
x = 0,3 |
|
1,0 + ……= 1,7 |
1,0 + x = 1,7 |
x =0,7 |
|
3,2 +…. .= 4,3 |
3,2 + x = 4,3 |
x = 1,1 |
|
13,6 + ……..= 23,7 |
13,6 + x = 23,7 |
x =10,1 |
|
35,9 + …… = 59,8 |
35,9 + x = 59,8 |
x =23,9 |
|
……. +
238,4 = 673,2 |
x. + 238,4
= 673,2 |
x =434,8 |
|
Cas: 6,3 + …… = 5,6 |
Cas: 6,3 + x
= 5,6 |
x = (-0,7)voir les décimaux relatifs) |
Répondez ,aussi , aux questions suivantes:
|
Quelle est
l'opération poser dans la colonne 1 |
addition |
|
Quel est le nom
donné au résultat |
somme |
|
Dans la deuxième
colonne on remplace "le trou" par "x" ,trouver la valeur à donner à "x" Quelle opération
doit on faire pour trouver la valeur
de "x" |
La soustraction du
nombre " somme" moins
l'autre nombre donné. |
|
|
|
|
SOS Cours |
|
Série: 9 |
II ) les Calculs suivants font intervenir des nombres décimaux non relatifs
(soustraction)
|
Compléter les opérations |
|
|
|
Colonne 1 |
Colonne 2 |
Colonne 3 |
|
0,1-… =
0, 1 |
0,1- x =
0,1 |
x =0,1 |
|
0,1 - 0,1 =….. |
0,1-0,1 = x |
x =0 |
|
0,8 - ….. = 0, 5 |
0,8 - x = 0,5 |
x = 0,3 |
|
1,7 - ……=
1,0 |
1,7 - x = 1,0 |
x =0,7 |
|
4,3 -…. .= 3,2 |
4,3 - x = 3,2 |
x = 1,1 |
|
23,7 - ……..= 13,6 |
23,7 - x = 13,6 |
x =10,1 |
|
59,8 - …… = 35,9 |
59,8 - x =
35,9 |
x =23,9 |
|
……. -
238,4 = 673,2 |
x - 238,4
= 673,2 |
x =434,8 |
|
|
|
|
Répondez aux questions suivantes:
|
Quelle est
l'opération poser dans la colonne 1 |
soustraction |
|
Quel est le nom
donné au résultat |
différence |
|
Dans la deuxième
colonne on remplace "le trou" par "x" ,trouver la valeur à donner à "x" Quelle opération
doit on faire pour trouver la valeur
de "x" |
La soustraction du
nombre " différence" moins
l'autre nombre donné. |
|
|
|
|
SOS Cours |
|
Série: 10 |
les calculs suivants font intervenir des nombres décimaux non relatifs
(multiplication)
|
Compléter les opérations |
|
|
|
Colonne 1 (à compléter) |
Colonne 2 |
Colonne 3 |
|
0,1 |
0,1 |
x =1 |
|
0,1 |
0,1 |
x =0,01 |
|
0,8 |
0,8 |
x = 5,0 |
|
1,7 ……=
17,0 |
1,7 x = 17,0 |
x =10 |
|
4,3 …. .= 17,2 |
4,3 x = 17,2 |
x = 4,0 |
|
23,7 ……..= 165,9 |
23,7 x = 165,9 |
x =7,0 |
|
59,8 …… = 777,4 |
598 x =
777,4 |
x =13,0 |
|
……. |
x |
x =13,4 |
|
|
|
|
Répondez aux questions suivantes:
|
Quelle est
l'opération poser dans la colonne 1 |
multiplication |
|
Quel est le nom
donné au résultat |
produit |
|
Dans la deuxième
colonne on remplace "le trou" par "x" ,trouver la valeur à donner à "x" Quelle opération
doit on faire pour trouver la valeur
de "x" |
La division du nombre
" quotient" moins
l'autre nombre donné. |
|
|
|
|
SOS Cours |
|
Série: 11 |
les calculs suivants font intervenir
des nombres décimaux non relatifs (division)
|
SOS Cours |
|
|
Compléter les
opérations |
|
|
|
Colonne 1 (à
compléter) |
Colonne 2 |
Colonne 3 |
|
1:… =
1 |
1: x
= 1 |
x =1 |
|
1 : 1 =….. |
1: 1 = x |
x =1 |
|
40 : ….. =
8 |
40 : x = 8 |
x = 5 |
|
170 :……=
17 |
170 : x = 17 |
x =10 |
|
172 :…. .= 43 |
172 : x = 43 |
x = 4 |
|
1659 :……..= 237 |
1659 : x = 237 |
x =7 |
|
7774 :…… = 598 |
7774: x = 598 |
x =13 |
|
319456 : ……
= 2384 |
319456: x = 2384 |
x =134 |
|
|
|
|
Répondez aux questions suivantes:
|
Quelle est
l'opération poser dans la colonne 1 |
multiplication |
|
Quel est le nom
donné au résultat |
produit |
|
Dans la deuxième
colonne on remplace "le trou" par "x" ,trouver la valeur à donner à "x" Quelle opération
doit on faire pour trouver la valeur
de "x" |
La division du nombre
" quotient" moins
l'autre nombre donné. |
|
|
|
|
SOS Cours |
TESTS D’ALGEBRE
N° 3
|
Série: 12 |
Les calculs suivants
font intervenir les nombres relatifs
|
SOS Cours |
|
|
résultat |
x |
|
|
|
|
|
(+7)+(+
4) = x |
x = (+11) |
|
|
(+7)+(-
4) = x |
x =(+3) |
|
|
(-7)+(+
4) = x |
x =(-3) |
|
|
(-7)+(-
4) = x |
x =(-11) |
|
|
|
|
|
|
(+7)-(+ 4) = x |
x =(+3) |
|
|
(+7)-(- 4) = x |
x =(+11) |
|
|
(-7)-(+ 4) = x |
x =(-11) |
|
|
(-7)-(- 4) = x |
x =(-3) |
|
|
|
|
|
|
(+7) |
x = ( +28) |
|
|
(+7) |
x = ( -28) |
|
|
(-7) |
x = ( +28) |
|
|
(-7) |
x = ( -28) |
|
|
|
|
|
|
|
x = (+1,75) |
|
|
|
x = (-1,75) |
|
|
|
x = (+1,75) |
|
|
|
x = (+1,75) |
|
|
|
x =(+ |
|
|
|
x =(- |
|
|
|
x =(+ |
|
|
|
x =(- |
|
|
|
|
|
|
Série: 13 |
Avant de résoudre il
faut transformer l ‘égalité donnée ;en
appliquant le produit en croix
|
SOS Cours |
|
|
Exercices , donner la valeur de "x" |
Réponses |
|
|
5x =12 |
|
|
7 |
|
|
7x=3 |
|
|
7 |
|
|
|
|
Utiliser pour calculer
la quatrième proportionnelle |
|
Série: 14 |
Les calculs
suivants font intervenir les nombres
relatifs
Suite
|
SOS Cours |
|
|
|
Compléter les
opérations |
|
|
|
Colonne 1 |
Colonne 2 |
Colonne 3 |
|
1-… =
1 |
1-
x = 1 |
x =0 |
|
1 - 1 =….. |
1-1 = x |
x =0 |
|
5 - ….. = 8 |
5 - x = 8 |
x = (-3) |
|
10 - ……= 17 |
10 - x = 17 |
x =(-7) |
|
32 -…. .= 43 |
32 - x = 43 |
x = (-11) |
|
136 - ……..= 237 |
136 - x = 237 |
x =101 |
|
359 - …… = 598 |
359 - x =
598 |
x =(-239) |
|
……. -
2384 = 6732 |
x
- 2384 = 6732 |
x =9116 |
|
Cas: 63 - …… =
56 |
Cas: 63 - x
= 56 |
x = 7 |
|
Série: 15 |
Les calculs
suivants font intervenir les "nombres
relatifs"
|
SOS Cours |
|
|
Résoudre |
|
|
|
7+ x = 1 |
|
X = -6 |
|
7 |
|
X= 4 |
|
7 -x = 3 |
|
X = 4 |
|
|
|
X= 12 |
|
|
|
X = 7 |
|
Série: 16 |
|
SOS Cours |
|
|
Résoudre |
|
Résultat sous forme
décimale à 0.01 prés |
|
7,2 + 4, 8 = x |
|
|
|
7, 2 |
|
|
|
7, 2- 4, 8 = x |
|
|
|
|
|
|
|
|
|
|
|
SOS Cours |
|
|
Résoudre : |
|
|
|
5,3x = 26,5 |
|
5 |
|
6x-3 + 15x =
17x -3 |
|
0 |
|
5(x-4) =
4 ( 2x+1) -
4 |
|
- 20 /3 |
|
5(2x+1) –3x +4 = 6 |
|
-3/7 |
|
2,5 x –3,7 = 2,3 (5 – 4,2x ) |
|
|
TESTS D’ALGEBRE
N° 4
|
Série: 18 |
|
Traduire (deux possibilités) |
|
|
|
Lire « x » puissance « y » ou " x " exposant « y » |
|
|
|
|
Série: 19 |
|
Puissances
: SOS
cours |
|
|
xx = |
x2 |
|
m |
m2. |
|
(dm) |
(dm)2 |
|
(cm) |
(cm)2 |
|
(mm) |
(mm)2. |
|
I |
II2. |
|
(AB) |
(AB)2. |
|
Série:20 |
Traduire en
langage littéral et transformer l ' écriture ( on peut
dire forme : développer )
|
|
|
|
x0 = |
x0 = x0= par convention x0 =1 |
|
x 1
= |
x 1 = x1=
x 1 , dans l’écriture courante x 1 = x |
|
x2 = |
x2 = x1 .
x2 = x2 , lire « x » puissance « 2 » ou
lire aussi « x »
« au carré » |
|
x3 = |
x3 = x1 . x2 . x3 = x3 , lire « x » puissance « 3 » ou
lire aussi « x »
« au cube » |
|
x4 = |
x4 = x1 .
x2 . x3 .
x4 = x4 , lire « x »
puissance « 4 » |
|
x5 = |
x5 = x1 . x2 . x3 . x4. x 5 = x5 , lire « x »
puissance « 5 » |
|
x6 = |
x6 = x1 . x2 . x3 . x4.
x 5 . x6 = x6 ,lire « x » puissance
« 6 » |
|
Série: 21 |
Mettre sous forme de puissances:
|
SOS Cours |
|
|
|
|
|
x |
x |
|
xx xx = |
xx xx
=x4 |
|
x |
x |
|
x |
x |
|
x |
x |
|
y |
y |
|
y |
y |
|
x |
x |
|
a |
a |
TESTS D’ALGEBRE
N° 5
|
Série: 22 |
Compléter les phrases suivantes:
|
SOS Cours |
|
|
Si « x » est positif quel sera le signe de x n : "n" est paire "x" sera : "n" est impaire "x" sera : |
si
« n » est impaire dans xn ; le résultat donné par le calcul de xn.....positif si « n » est paire dans xn ;
le résultat donné par le calcul de xn
est positif. |
|
b) -
Si « x » est négatif
quel sera le signe de " x n ". "n" est paire "x" sera : "n" est impaire "x" sera : |
cas 1 : si
« n » est impaire dans xn ; le résultat donné par le calcul de xn.....négatif............... Cas 2 : si « n » est paire dans xn ;
le résultat donné par le calcul de xn
est positif. |
|
Série: 23 |
|
SOS Cours |
|
|
|
|
|
Un carré est toujours ......... |
Un carré est toujours
.........positif................. |
|
00 est une forme ...... |
00 est une forme ...... « indéterminée »..... |
|
0 n =
............ |
0 n =
............ 0 ( n différent
de 0 )... |
|
L’inverse de x1 est :…………………… |
|
|
x -1 = |
x -1 = |
|
Série: 24 |
|
SOS Cours |
|
|
Compléter les égalités: |
Réponses |
|
|
|
|
|
|
|
|
|
|
Série: 25 |
|
SOS Cours |
|
|
Compléter les égalités: |
Réponses |
|
|
|
|
|
|
|
|
|
TESTS D’ALGEBRE
N° 6
|
Série: 26 |
transformer
l’expression en somme algébrique contenant des « x »
|
SOS Cours |
|
|
L’expression algébrique |
devient la somme algébrique |
|
3x +5 |
(+3x) + (+5) |
|
-5x2 + 3x -6 |
(-5x2) + (+3x)+(-6) |
|
7
a x2 - 3 by |
(+7ax2 ) + (
-3 by) |
|
3x -12y + |
(+3x) + (-12y) + (+ |
|
|
|
|
Série: 27 |
Calculer le PGCD de :
|
SOS Cours |
|
|
|
PGCD |
|
2 et 4x |
2 |
|
2a et ab |
a |
|
a et ad |
a |
|
6b et 3b |
3b |
|
3x et x
y |
x |
|
a2
b ; c b |
b |
|
a2bd
; ac2fd |
ad |
|
2x2y
et 4xy2 |
2xy |
|
(x-3)
(x+1) et 3(x -2) (x+1) |
( x+1) |
|
Série: 28 |
|
SOS Cours |
|
|
|
|
|
2 + 4x |
2 ( 1 +2x ) |
|
2a +ab |
a( 2 + b ) |
|
a - ad |
a(1-d) |
|
6b + 3b |
3b(2 +1 ) |
|
3x
- x y |
3 ( x -y ) |
|
a2 b + c b |
b (a2 + c ) |
|
a2bd + ac2fd |
a (a b + c2f) |
|
2x2y - 4xy2 |
2 xy ( x - 2y) |
|
(x-3) (x+1) +
3(x -2) (x+1) |
( x+1) ( (x-3) + ( x-2 ) ) |
|
Série: 29 |
Développer :
|
SOS Cours |
|
|
|
|
|
2 ( 1 +2x
) |
2 + 4x |
|
a( 2 + b ) |
2a +ab |
|
a(1-d) |
a - ad |
|
3b(2 +1 ) |
6b + 3b |
|
3 ( x -y
) |
3x - x y |
|
b (a2 + c ) |
a2 b + c b |
|
a (a b + c2f) |
a2bd + ac2fd |
|
2 xy ( x - 2y) |
2x2y - 4xy2 |
|
( x+1)
( (x-3) + ( x-2 ) ) |
(x-3) (x+1) + 3(x -2) (x+1) |
exercices: voir livre
Mathématique - tome 1 -
algèbre ;préparation BEP .
page
23 ; n°9;10;11;12;13;14;15.
éditeur : Fernand Nathan ;1970.
TESTS D’ALGEBRE
N° 7
|
Série: 30 |
Rendre irréductible les expressions
suivantes :
|
SOS Cours |
|
|
|
Résultat: |
|
|
|
|
|
|
|
|
|
|
Série: 31 |
calculer : voir produit de nombres relatifs
|
SOS Cours |
|
|
Faire le produit de : |
|
|
(-2x) (+3) |
(-6x) |
|
(-2 x) (+3) ( -1,5)
|
(+9x) |
|
(4x) (2x) |
(+8x2) |
|
(4x) (-2,1 x)(-4)
|
(+31,6 x2) |
TESTS D’ALGEBRE
N° 8
|
Série: 32 |
Calculer "A" à partir
de l’expression suivante: voir puissance d'opérations simples
|
SOS Cours |
|
A = 2x3
+3x2 - x + 7
|
Remplacer "x" par la valeur donnée et
effectuer les calculs |
|
|
x
= +1 |
2+2-1+7=10 |
|
x = 0 |
0+0-0+7=7 |
|
x = +0,1 |
0,002+0,03 -0,1+7 =6,932 |
|
x = -1 |
-2+3+1+7 =9 |
|
x= 3 |
54+27-3+7 =85 |
|
x= -2,8 |
-43,904+23,52+2,8+7=
-10,584 |
TESTS D’ALGEBRE
N° 9
|
Série: 33 |
Mettre au même
dénominateur les écritures fractionnaires suivantes:
|
SOS Cours |
|
|
Calcul du PPDC des
dénominateurs 3x;2x;
x =
6x
|
|
|
Le PPDC de 3x et 3y
est "3xy"
|
|
|
Le PPDC de 3x2 et 2x est "6x2"
|
|
Série: 34 |
|
CALCULER |
|
|
|
-74 / 3x |
|
|
-9 /3x |
|
|
1 / x2 |
|
|
x / 4y |
|
|
5x2 / (4y2 +1) |
|
|
(3x-4y
) /2x2 |
|
|
( 3 (x-y)) / 2x2 |
|
|
-1 / x2 |
|
|
|
|
|
|
|
|
|
|
- 6x /13 |
|
|
|
1 / 2x |
|
|
|
(8x-7)/(2x+1) |
4°) Faire les soustractions
suivantes : (pour
pouvoir regrouper les termes en numérateur il faudra revoir l’objectif sur
« Factoriser - développer »
|
Série 35 |
|
SOS Cours |
|
|
|
|
Réponses |
|
a ) |
|
x / 4y |
|
b ) |
|
5x2 / (4y2
+1) |
|
c ) |
|
(3x-4y ) /2x2 |
|
d ) |
|
( 3 (x-y)) / 2x2 |
|
e ) |
|
-1 / x2 |
|
Série: 36 |
Niveau III: Faire les multiplications suivantes
|
SOS Cours |
|
|
Série 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Série: 37 |
Faire les multiplications suivantes :
|
SOS Cours |
|
|
Série 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Série: 38 |
|
SOS Cours |
|
|
|
|
|
|
12,5x |
|
125x/10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Série: 39 |
Algèbre : mettre sous
forme de fraction irréductible le produit suivant:
|
SOS Cours |
|
|
0,5x |
|
5x/10 = x/2 |
|
3,5x |
|
35x/10 |
|
0,75x |
|
75x/100 =3x/4 |
|
1,5x |
|
15x/10 =3x/2 |
|
Série: 40 |
Les exercices suivants sont rencontrés lorsque
nous travaillerons la fonction affine
|
SOS Cours |
Prérequis |
|
|
|
|
|
(x+9) / 3 |
|
|
(-x +14) /
2 |
|
|
(-2x +9) / 3 |
|
|
( 10 x + 96 ) / 30 soit (5x+ 48 ) / 15 |
|
|
( - 5 x + 7 ) / 10 |
|
|
(-4 x + 9 ) / 6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Série: 41 |
ADDITION
|
SOS cours |
|
|
Réponses : |
|
|
|
|
|
|
|
|
|
|
Série: 42 |
Faire les
soustractions suivantes :
(pour pouvoir regrouper les termes en numérateur il faudra revoir
l’objectif
sur « Factoriser - développer »
|
SOS Cours |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
TESTS D’ALGEBRE
N° 10
|
Série: 43 |
|
SOS Cours |
Racines
carrées |
||||
|
|
|
|
|
||
|
( |
x |
|
|
||
|
( |
x2 |
|
|
||
|
|
|
= 2 = 10 |
Traduction littérale: La racine carrée d’une
multiplication est égale à la
multiplication des racines carrées. |
||
|
|
|
|
|
||
|
|
|
|
|
||
|
|
|
|
|
||
|
|
|
|
|
||
|
|
|
|
|
||
|
|
Aucune transformation possible |
|
|
||
|
|
Aucune transformation possible |
|
|
||
|
|
Aucune transformation possible |
|
|
||
|
|
Aucune transformation possible |
|
|
||
|
|
|
|
|
||
|
Série: 44 |
|
SOS Cours |
Racines
carrées |
|
|
|
|
|
|
|
5 |
|
|
|
2 |
|
|
|
2x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( |
|
|
|
|
|
|
|
|
|
|
|
Racines
carrées |
|
7 = |
7 2
= ( |
: 7
2 = 30+x 49 = 30+x 49 -
30 = x ;
19 = x ; conclusion
« x » vaut 19 |
|
50 = |
50 2
= ( |
50 2
=1600+x2 2500 - 1600 = x2
30 = x |
|
Série: 46 |
|
SOS Cours |
Racines
carrées |
Evaluation: remplacer dans les lettres par les nombres
suivants et faire le calcul :
avec x= 16
et y = 9
|
|
|
|
|
|
( |
x |
|
|
|
( |
x2 |
|
|
|
|
|
= 2 = 10 |
Traduction
littérale: La racine carrée d’une
multiplication est égale à la
multiplication des racines carrées. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Aucune
transformation possible |
|
|
|
|
Aucune
transformation possible |
|
|
|
|
Aucune
transformation possible |
|
|
|
|
Aucune
transformation possible |
|
|
|
Série: 47 |
Première série d ’exercices
:
|
SOS Cours |
Racines
carrées |
soit un nombre « x » ;
trouver la racine carrée du nombre :
|
|
|
|
|
x =0,25 |
|
0,5 |
|
x = 7,29 |
|
2,7 |
|
x = 33,64 |
|
5,8 |
|
x = 81 |
|
9 |
|
x = 291
600 |
|
540 |
|
x = 2 744
000 |
|
1656,502339 |
|
x =
1,5746 |
|
39681,22982 |
|
Série: 48 |
II
)Deuxième série d’exercices en relation avec la racne
carrée d’un produit:
|
SOS Cours |
Racines
carrées |
|
|
|
|
|
|
|
4 fois 5
=20 |
|
|
|
|
|
|
|
|
|
|
|
=630 |
|
|
|
=1600 |
|
|
|
=600 |
TESTS D’ALGEBRE
N° 11
|
Série: 49 |
On dit que :
|
Dans un triangle rectangle le
"carré" du grand coté
(hypoténuse) est égal à la somme
des "carrés" des
longueurs des cotés formant l’angle droit . |
Ceci
étant dit ,
calculer l’hypoténuse d’un triangle rectangle
dont les cotés de l’angle droit valent
respectivement:
|
SOS Cours |
Racines
carrées |
|
1 °) 8
cm et 6 cm |
a = |
a = |
a =10 cm |
|
2°) 12 m
et 9 m |
a = |
a = |
15 |
|
3°) 165
mm et 92 mm |
a = |
a = |
188,91532 |
|
4°) 125m
et32,7dam |
a = |
a = |
350,07713 |
|
Série: 50 |
B ) L’hypoténuse
d’un triangle rectangle se calcule en utilisant
la formule suivante:
a =![]() ; dans laquelle b et
c sont les mesures des deux cotés
formant l’angle droit.
; dans laquelle b et
c sont les mesures des deux cotés
formant l’angle droit.
I ) Calculer la longueur de l’hypoténuse d’un
triangle rectangle dont les longueurs des cotés de l’angle droit sont :
|
c =
0,35 dm et
b = 0,84 dm a = donc : a2
= b2 + c2 |
donc : a2
= 0,842 + 0,352 calcul: 0,842=0,7056 0,352=0,1225 a2
=0,8281 a = a=0,91 dm |
|
|
|
|
|
|
Série: 51 |
II ) Calculer la
longueur du coté c , sachant que
|
a = 50
cm et
b = 30cm a = donc : a2
= b2 + c2 |
502
= 302 + c2 2500 =
900 + c2 2500 -900
= c2 1600 = c2
c = 40 cm |
|
|
|
|
|
|
Série: 52 |
III ) Calculer la
longueur du coté b , sachant que
|
c= 24
dm et
a= 400mm a= 40 dm a = donc : a2
= b2 + c2 |
402
= b2 + 242 402 - 242 = b2 1600
- 576 = b2 1024
= b2
32 = b |
|
|
|
|
|
AIRE:
|
Série: 53 |
Carré: l ’
aire d’un carré est de
2735,29 dm2
question
: donner la valeur de la mesure d’un
coté en dm puis mm
|
C = |
52,3dm |
5230mm |
|
|
|
|
|
Série: 54 |
Cercle et disque :
a) Calculer le rayon d’un cercle dont l’aire est
de 2826
cm2
On
prendra 3,14 pour « py »
|
Aire du
disque = 3,14R2 |
2826 cm2 = 3,14 R2 |
R2
= 2826:3,14 |
|
|
|
R2
=900 cm2 |
|
R = |
R = 30 cm |
|
b) Calculer
la valeur du diamètre d’un cercle dont l’aire est de 14949,54 cm2
On
prendra 3,14 pour « py »
Solution
1 : on prend l'Aire du disque = 3,14R2
|
D = 2R |
|
|
|
Aire du
disque = 3,14R2 |
14949,54
= 3,14 R2 |
R2
= 14949,54:3,14 |
|
|
|
R2
=4761cm2 |
|
R = |
R = 69 cm |
Donc D =
138 cm |
Solution
2: on prend l'Aire du disque = 3,14(D2/4 )
On trouve D
= 138 cm
|
Série: 54 |
ELECTRICITE:
La
puissance électrique consommée dans une
résistance est donnée par la formule
P
= R x I2 dans laquelle R est la mesure de la résistance et I
celle de l’ intensité.
A)transformer la formule pour que nous puissions calculer I
( I = ? )
Calculer
l’intensité « I » si P = 4050
Watts et R = 8 ohms
|
P = R x
I2 |
4050 = 8
x I2 |
|
|
|
|
|
|
I = |
|
I =
22,5 ampères |
|
I = 22,5
A |
|
|
|
Série: 55 |
Application de la racine carrée en sciences
I ) Calcul d’aire d'un carré est de 81 m2
Type d’exercice :
Rechercher la longueur du coté d’un
carré ( petit cé « c »)dont on connaît son aire
(« cé »
au carré s’écrit en langage mathématique: c 2
).
|
Comme c 2=81 |
|
|
pour
trouver « c »; j’écrirai
que |
|
|
c = |
c = |
|
|
c= 9 c = soit
plus simplement : 9 m |
|
conclusion
:le carré de
81 m2 à pour coté 9 |
|
FIN de la première
série de tests:
|
TESTS N° 2 |