Définition du mot "formule"

Série 1 :

Activités : il n’y a pas de formules à transformer ; Il faut remplacer les lettres par les valeurs données et faire le calcul .

Calcul numérique : N°1 (remplacer « x » par sa valeur et calculer)
Calcul numérique : N°2 (calculs numérique d’une expression algébrique) avec a) des nombres ; b) des grandeurs
AIRES et VOLUMES : réservés aux élèves de BEP Bac prof calculs directs
Calculs numériques (sans parenthèses)
Suites d’opérations et priorités

Série 2 :

Il y a une transformation de la « formule ».

Dans un premier temps ,on remplace les lettres (sauf une ) par les valeurs données. Il faut alors « isoler » la lettre ( inconnue) . En algèbre, on dit « résoudre ».

Calculs algébriques
Les égalités EG1 : vocabulaire	cliquez ici
Les égalités EG2 : vocabulaire : membre ;….	cliquez ici
Les égalités EG 3 : les éléments neutres et neutralisation d’un terme ou d’un facteur.	cliquez ici
Les égalités EG4 : les théorèmes de transformation.	cliquez ici
Les éléments et ensembles	cliquer ici

ENVIRONNEMENT du dossier:

INDEX

1°) Objectif précédent

2°) voir calculs numériques

Objectif suivant :

1°) calculs numériques

2°) Autres calculs de niveau IV

Tableau : les égalités présentation

Autres : exercices

DOSSIER LES EGALITES et les Sciences

Définition du mot "formule"

LES EGALITES (SCIENCES)

Cet objectif a pour but de vous aider à vous familiariser aux "formules" de sciences.

Toutes ces formules peuvent se transformer, en dehors du sens que l' on peut leur donner.

Domaines :	Liste des objectifs « cours »	Formulaires
I ) Périmètre	Informations	Informations
II ) Aire	Informations	Informations
III ) Volume	Informations	Informations

SERIES

Compléter les égalités suivantes.

Applications numériques

PERIMETRES ;AIRES et VOLUMES

Carré

info

soit 4 a = P

trouver :

4 = ; a =

1°) calculer le périmètre d’un carré dont le côté mesure 15 m.

2°) le périmètre d’un carré mesure 60 mm quel est la longueur d’un des côtés ?

Rectangle

info

Soit 2( L + l ) = P

trouver :

L+ l =

l =

L =

1°) un rectangle a pour longueur 15 cm et pour largeur 8,4 cm .calculer son périmètre .

2°) le périmètre d’un rectangle est de 60 m ; sa longueur est de 18 m ; quelle est la dimension de sa largeur ?

3° ) °) le périmètre d’un rectangle est de 60 m ; sa largeur est de 10 m ; quelle est la dimension de sa longueur ?

4°) un rectangle a pour longueur 15 cm et pour largeur 8,4 cm .calculer la dimension de son ½ périmètre

Cercle

info

soit 2 p R = P

trouver :

2 =

R =

p =

cas : pi = 3,14

1°) un cercle à pour rayon 3m calculer sa circonférence . ( périmètre).

2°) la circonférence d’un cercle est de 314 cm . quel est la longueur du rayon ?

cas : prendre le « pi » de la calculatrice.

Donner le résultat au 1/100 prés

.1°) un cercle a pour rayon 3m calculer sa circonférence . ( périmètre).

2°) la circonférence d’un cercle est de 314 cm . quel est la longueur du rayon ?

cas : prendre le « pi » de la calculatrice.

Donner le résultat au mm prés.

1°) un cercle a pour rayon 3m calculer sa circonférence . ( périmètre).

2°) la circonférence d’un cercle est de 314 cm . quel est la longueur du rayon ?

soit D = 2R

trouver :

R =

2 =

info

1°)Le rayon d’un cercle est de 3m que est la longueur de son diamètre.

2°) Le diamètre d’un cercle est de 3,14m que est la longueur de son rayon ?

soit P = p D

trouver :

p =

D =

info

cas : pi = 3,14

1°) un cercle à pour diamètre 3m .Calculer sa circonférence . ( périmètre).

2°) la circonférence d’un cercle est de 314 cm . quel est la longueur du diamètre ?

cas : prendre le « pi » de la calculatrice.

Donner le résultat au 1/100 prés

.1°) un cercle a pour diamètre 3m calculer sa circonférence . ( périmètre).

2°) la circonférence d’un cercle est de 314 cm . quel est la longueur du diamètre ?

cas : prendre le « pi » de la calculatrice.

Donner le résultat au mm prés.

1°) un cercle a pour diamètre 3m calculer sa circonférence . ( périmètre).

2°) la circonférence d’un cercle est de 314 cm . quel est la longueur du diamètre ?

PERIMETRES ;AIRES et VOLUMES

Carré :

info

soit S = a a

trouver :

a =

1°) calculer l’aire d’un carré dont le côté mesure 15 m.

2°) l’ aire carré mesure 100 mm² quelle est la longueur d’un des côtés ?

soit S = a²

trouver :

a =

info °) calculer l’aire d’un carré dont le côté mesure 15 m.

2°) l’ aire carré mesure 1000 mm² quel est la longueur d’un des côtés ? (résultat au 1/100 prés).

3°) l’ aire carré mesure 2600 mm² quelle est la longueur d’un des côtés ? (résultat au mm prés)

soit S = a a

trouver :

a =

info Aire d’un carré :

1°) calculer l’aire d’un carré dont la longueur d’un côté est de 7 cm.

2°) l’ai d’un carré est de 169 cm³ . Quelle est la longueur d’un côté ?

Rectangle :

info aire d’un rectangle :

soit S = L l

trouver :

L =

l =

1°) un rectangle a pour longueur 15 cm et pour largeur 8,4 cm .calculer son aire . (126 cm²)

2°) l’aire d’un rectangle est de 195 m² ; sa longueur est de 1 5 m ; quelle est la dimension de sa largeur ? ( 13m)

3° ) l’aire d’un rectangle est de 120 m² ; sa largeur est de 10 m ; quelle est la dimension de sa longueur ?

4°)l’aire d’ un rectangle est de (126 cm²) a pour largeur 8,4 cm . Quelle est la longueur de son périmètre ?

(L = 15 cm ; P = 46,8 cm)

Triangle

info Aire d’un triangle .

soit := S

trouver :

B =

h =

l°)la base d’un triangle mesure : 15 m ; la hauteur 12 m ; quelle est la valeur de son aire ? ( 90)

2°) l’aire d’un triangle est de 185,6 cm² ; sa base est de 16 cm ; que est la longueur de sa hauteur ? ( 11,6 cm)

Disque :

info Aire d’un disque .

Soit p R R = S

trouver :

R =

cas : pi = 3,14

1°) un cercle à pour rayon 3m calculer son aire . ( 314 m²)

2°) l’ aire d’un disque est de 314 cm² . quel est la longueur du rayon ? 10 cm

cas : prendre le « pi » de la calculatrice.

Donner le résultat au 1/100 prés

.1°) un disque a pour rayon 3m calculer son aire .

28,27 m²

2°) l’ aire d’un disque est de 15 , 39 cm² . quel est la longueur du rayon ? ( 2,21 cm)

cas : prendre le « pi » de la calculatrice.

Donner le résultat au mm prés.

1°) un disque a pour rayon 3m calculer son aire .(28,274334 m²)

2°) l’aire d’un disque de 300 cm² . quel est la longueur du rayon ?(9,8 cm)

Soit

p R ² = S

trouver :

R =

info cas : pi = 3,14

1°) un cercle à pour rayon 3m calculer son aire . ( 314 m²)

2°) l’ aire d’un disque est de 314 cm² . quel est la longueur du rayon ? 10 cm

cas : prendre le « pi » de la calculatrice.

Donner le résultat au 1/100 prés

.1°) un disque a pour rayon 3m . Calculer son aire .

28,27 m²

2°) l’ aire d’un disque est de 15 , 39 cm² . Quelle est la longueur du rayon ? ( 2,21 cm)

cas : prendre le « pi » de la calculatrice.

Donner le résultat au mm prés.

1°) un disque a pour rayon 3m calculer son aire .(28,274334 m²)

2°) l’aire d’un disque de 300 cm² .Quelle est la longueur du rayon ?(9,8 cm)

Soit S = (p D²)/ 4

Ou S =

trouver :

D =

info cas : pi = 3,14

1°) un cercle à pour diamètre 6m calculer son aire . ( 314 m²)

2°) l’ aire d’un disque est de 314 cm² . quel est la longueur du diamètre ? 20 cm

cas : prendre le « pi » de la calculatrice.

Donner le résultat au 1/100 prés

.1°) un disque a pour rayon 6 m calculer son aire .

28,27 m²

2°) l’ aire d’un disque est de 15 , 39 cm² . quel est la longueur du diamètre ? ( 4,42 cm)

cas : prendre le « pi » de la calculatrice.

Donner le résultat au mm prés.

1°) un disque a pour diamètre 6 m calculer son aire .(28,274334 m²)

2°) l’aire d’un disque de 300 cm² . quel est la longueur du diamètre ?(19,6 cm)

Trapèze :

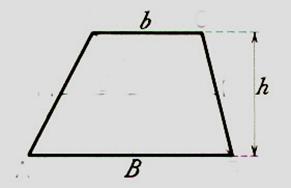
Aire d’un trapèze :

Soit = S

trouver :

(B + b) =

h =

B =

b =

1° ) Calcul d’aire du trapèze

Un trapèze a les dimensions suivantes : B = 12,6 cm ; b = 7,4 cm ; h = 6,8 cm.

Calcul de son aire .A = = 68 cm²

2°) Calcul d’une dimension : hauteur du trapèze

La hauteur du trapèze s’obtient en divisant l’aire de la surface par la demi somme des bases . soit :

Application : Trouver la hauteur du trapèze qui à une aire de 50 m² et dont les bases mesurent 12,6 m et 7,4 m

Hauteur = == 5 m

3°)Calcul d’une dimension : une des bases du trapèze

pour trouver la dimension d’une base , on recherche par calcul d’abord la somme des bases ; pour cela on divise l’aire par la moitié de la hauteur. Puis de la somme des bases on retranche la valeur de la base connue.

soit :

Application : Un trapèze a 27 m² d’aire , la hauteur mesure 5m, et l’une des bases 4 m . Calculer l’autre base.

a) = = 10,8 m

b) base cherchée = somme des bases – base connue

= 10,80 – 4 = 6,80 m

Calculer l’aire du trapèze :

B = 54 cm

b = 18 cm

h = 24,5 cm

PERIMETRES ;AIRES et VOLUMES

Cube :

Volume d’un cube

1°) soit V = a³

trouver :

a =

Exercices

1°)la longueur de l’arête d’ un cube est de 2,5 m. Calculer son volume .

2°) un cube a pour volume 27 m ³ . Quelle est la longueur d’une arête ?

2°) soit V = a² a

trouver :

a =

Volume d’un cube

pas de solution immédiate. Pour trouver « a » ; il faut passer par le « a au cube » ;

nota : pour trouver « a » on peut passer par « a au carré »

3°) Soit S .a = V

trouver :

S =

a =

Volume d’un cube

On donne l’aire de base d’un cube : 144 cm² ; calculer son volume .

Résolution : on fait la racine carrée de 144 , pour avoir la longueur de « a » ( 12 cm ) ; On fait le produit de « S » par 12 = 1728 cm³

Sphère :

info

Volume d’une sphère

V = 4 pr²r

trouver :

p =

r =

exercices

Cône :

Volume d’un cône :

soit V =

trouver :

p =

R =

h =

Exercices :

Formule :

V = ( R² + R’² + RR’)

On donne R = ;

R’ =

trouver : h

Volume du tronc de cône .

1°) Soit un tronc de cône : h = 15 cm ; R = 5cm ; R’ = 2cm ; calculer son volume

Formule : V = pR² H

Volume d’ un cylindre :

Formule : V = Ll h

Volume d’un parallélépipède rectangle

Soit a =

trouver :

A identifier

Electricité :
soit (1 ) U = R I trouver : R = I =	Cours
Puissance (2 )soit P = U I ² trouver : U = I =	Cours
En remplaçant « U » de (1) dans (2) par Calculer « R » en fonction de « P » et « I »
Mécanique:	Poids et masse
P = mg m = ? g = ?
Cinématique :	mouvement accéléré.
e =gt²+v_ot+e_o
Cinématique :	le mouvement uniforme
e = v t v = ? t = ?

PYTHAGORE
Soit : b ² + c² = a² trouver : a = b² = c ²= b = c =
AC² = AB ² +BC ² ; trouver : AB² = BC ² = AC = AB = BC =
Relations trigonométriques dans le triangle rectangle .
soit sin µ = trouver : a = b =				Le sinus d’un angle
soit cos µ = trouver : a = b =				Le cosinus d’un angle
soit tg µ = trouver : sin µ = cos µ =				La tangente d’un angle
soit : c₁ = 2 R₁ sin trouver : R₁ = sin =
soit : f₂ = R₂(1 - cos ) trouver : R₂= cos =
Les POURCENTAGES:
soit : y = x trouver : x = a =				Cours « a% d’un nombre »
soit : y = () x trouver : x = ; a =				Cours : « augmentation »
soit : y = () x trouver : x = a =				Cours : « diminution »
THALES				Cours :
Calculer la valeur de « x » : = Calculer la valeur de « x » ; « y » ; z » : = ==
ECHELLES				Info +++
Ech.. = trouver : dp = ; dr =
Dr		4,5 km	4,5 cm	0.02 mm
Ech.	1 / 20 000	1 : 50 0000
Dp	69 cm		9 mm	0.04 m