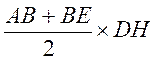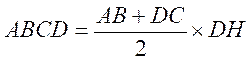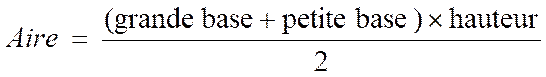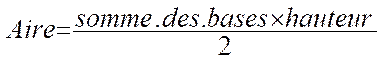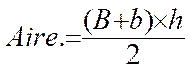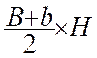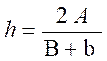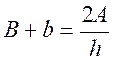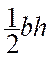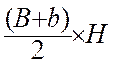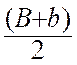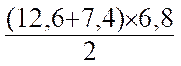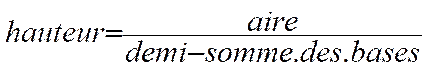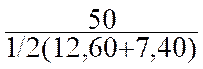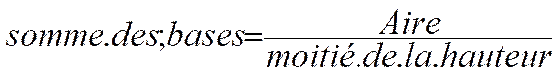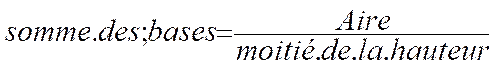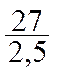Le trapèze

Conversion

Index   warmaths     

Objectif précédent   le trapèze :

Objectif suivant : 

Liste des cours sur les surfaces élémentaires .

Liste des calculs

DOSSIER : Calcul de l’ Aire du trapèze.

TEST

COURS

Devoir  Contrôle

Devoir évaluation

Interdisciplinarité

Corrigé Contrôle 

Corrigé évaluation 

TRAVAUX et CALCULS : niveau VI et V

Dos 135

Devoir

COURS

Exercice préliminaire :

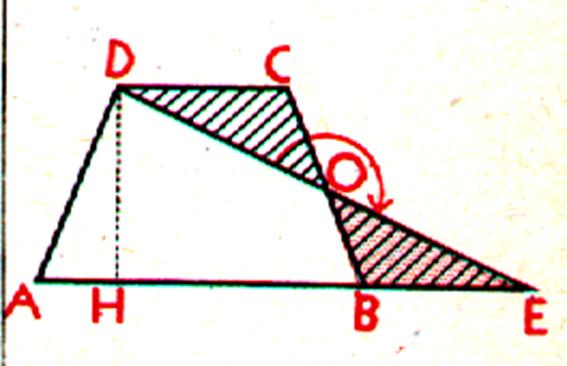
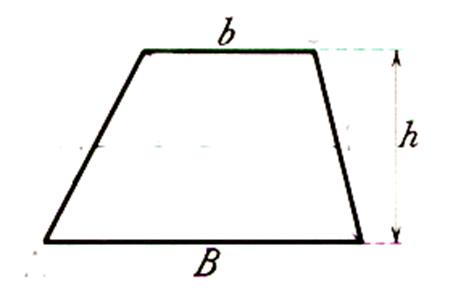
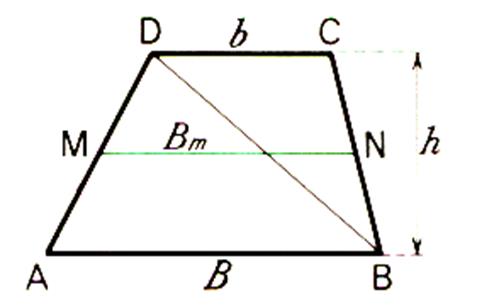
Soit le trapèze ABCD. Prenons le milieu O du coté BC , la droite DO coupe en E le coté AB prolongé ; nous vérifions  que l’aire du trapèze ABCD est égale à celle du triangle ADE.

Nous pouvons écrire : Aire ABCD = aire ABOD + aire DCO

L’aire ADE = aire  ABOD + aire BOE

Si nous décalquons le triangle  DOC et faisons tourner le calque de 180° autour su point O ; le triangle DOC vient se superposer au triangle OBE , donc :

Aire DCO = aire BOE

Et l’aire ABCD = aire ADE

Mais l’aire ADE =

or : DC = BE

donc : l’ aire  du trapeze est égale à :

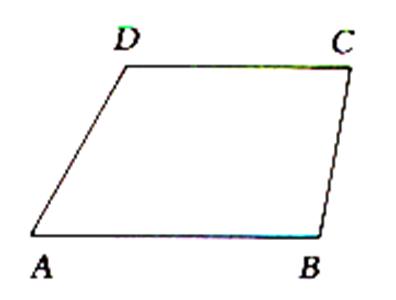
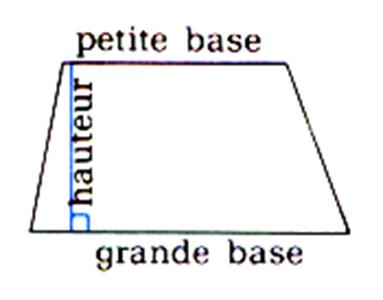
Définition :     Le trapèze est un quadrilatère !

A savoir :  

Pour calculer l’aire d’un trapèze  il faut connaître la longueur de la petite base , de la grande base et de la hauteur .

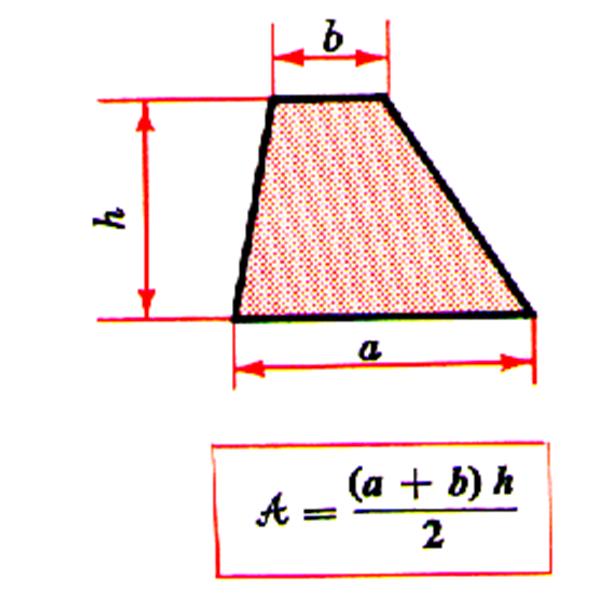
L ‘ aire d’un trapèze est égale au produit de la somme des longueurs  de la petite base et la grande base par la longueur de la hauteur ce produit est ensuite divisé par  deux .

Remarque : les longueurs doivent être exprimées dans la même unité de longueur

On dit que :

ou

 ;

en abrégé :

ou sous forme littérale :  

S =

On peut en déduire :   (On désigne  l’aire par la lettre « A »)

     et  

l’ aire  du trapèze égale au demi - produit de la somme des bases par le hauteur.

L’aire du triangle ABCD de base AB = B et CD = b et de hauteur « h » est égale à la somme des aires des triangles ABD est BCD :

 donc

S =  +   ou   S =

On désigne  par B_m   la base moyenne :

MN =

Nous pouvons écrire  la formule :

S = B_m h

Exemples de calculs

1°  ) Calcul d’aire  du trapèze

Un trapèze a les dimensions suivantes : B = 12,6 cm ; b = 7,4 cm ; h = 6,8 cm.

Calcul de son aire .

A  =  = 68  cm²

2°) Calcul d’une dimension : hauteur du trapèze

La hauteur du trapèze s’obtient en divisant l’aire de la surface par la demi somme des bases . soit : 

Application : Trouver la hauteur du trapèze qui à une aire de 50 m² et dont les bases mesurent 12,6 m et  7,4 m 

Hauteur =  == 5 m

3°)  Calcul d’une dimension : une des bases du trapèze

pour trouver la dimension d’une base , on recherche par calcul d’abord la somme des bases ; pour cela on divise l’aire par la moitié de la hauteur. Puis de la somme des bases on retranche la valeur de la base connue .

soit :

Application : Un trapèze a 27 m² d’aire , la hauteur mesure 5m, et l’une des bases 4 m . Calculer l’autre base.

a)   =  = 10,8 m

b) base cherchée = somme des bases – base connue    = 10,80 – 4 = 6,80 m

TRAVAUX AUTO FORMATIFS.

CONTROLE :

1 ) A quoi est égale l’ aire du trapèze  ?

2 ) Donner la formule permettant de calculer l’aire d’un carré (compléter avec un dessin coté )

EVALUATION

1°  ) Calcul d’aire  du trapèze

Un trapèze a les dimensions suivantes : B = 12,6 cm ; b = 7,4 cm ; h = 6,8 cm.

Calculer  son aire .

2°) Calcul d’une dimension : hauteur du trapèze

Trouver la hauteur du trapèze qui à une aire de 50 m² et dont les bases mesurent 12,6 m et  7,4 m 

3°)  Calcul d’une dimension : une des bases du trapèze

Un trapèze a 27 m² d’aire , la hauteur mesure 5m, et l’une des bases 4 m . Calculer l’autre base.

  4°)   Suite :    Trapèze et équation du premier degré.

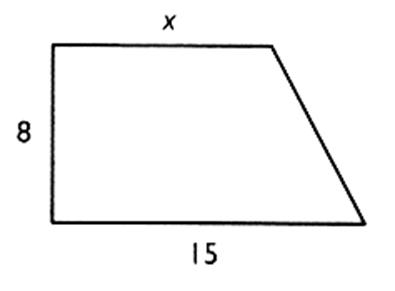
Montrer que l'expression de l'aire du trapèze rectangle en fonction de "x" est :

 A = 4 x + 60

Calculer "x" pour que l'aire du trapèze rectangle soit égale à 200 cm² . Pour cela , résoudre l'équation : 4x + 60 = 200

INTERDISCIPLINARITE

1° )Un champ a la forme d’un trapèze ; la grande base mesure 120 m , la petite base 50 m et la hauteur 50 m , il a été estimé a 10 000 € l’are . Donnez en le prix .

2° ) Un terrain a la forme d’un trapèze a été vendu 39 37, 5 €  à raison de 7,5   €  le m². Ce terrain a la forme d’un trapèze dont la hauteur a 25 m et l’une des bases 17,5 m . Quelle est la longueur de l’autre base ?

3°) ,Une lame de cutter en forme de trapèze a des bases mesurant 65 mm et 42 mm et une hauteur de 36 mm . Calculer son aire en mm² et en cm².

4°) Un jardin de forme trapézoïdale à une aire de 2100 m²  . Ses bases mesurent 45 m et 25 m . Quelle est la mesure de sa hauteur en m . (Construire ensuite la figure à l’échelle  1/100 .)

5°) Une pièce de tissus trapézoïdale à une grande base mesurant 3,50 m , une petite base de 21 dm et une hauteur de 120 cm .Quelle est son aire en m² ?