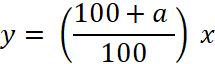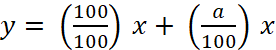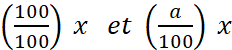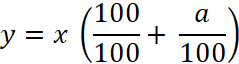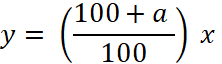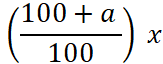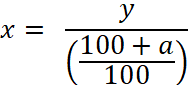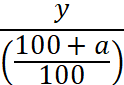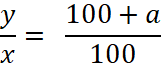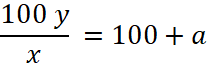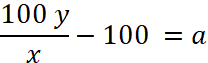|
|
COURS :
|
|
|
|
Comment passer d’une formulation additive à une formulation
multiplicative
Exemple :
on augmente de 5% un prix ; on ajoute 5% du prix au
prix de base , ou pour obtenir le
nouveau prix directement il suffit de multiplié l’ancien prix par
« 1 ,5 »
|
|
|
|
Objectif :
Augmentation en a%
|
|
|
|
|
|
|
|
INFO :
Définition de l ’ Objectif : Savoir trouver la Nouvelle
Grandeur ( NG)
d’une Grandeur de Départ (GD) ayant subit une augmentation de a% .
Cas de la vie
courante : sur une affiche on lit :
|
|
|
|
|
à vendre :
1200 € hors taxe
(taxe 25%)
|
|
|
|
|
Quelle somme réelle doit - on verser ?
les
réponses seront données à la fin du cours !
Pour trouver la « Nouvelle
Grandeur »(prix après augmentation) d’une
« Grandeur de Départ » (prix avant augmentation) ayant subit une
augmentation , il faut :
n que la « Grandeur de Départ » (prix avant augmentation) notée (GD) représente 100% de sa valeur de
départ.
n que
l ‘ « augmentation» (différence entre le prix avant
augmentation et le prix après augmentation) représente
« a% » de cette
« Grandeur de Départ »
(prix avant augmentation).
On
peut ainsi conclure que :
Le prix à
payer : c’est à dire La Nouvelle
Grandeur (NG) sera égale à 100 / 100
de la grandeur de départ (GD)
plus le « a % « de cette Grandeur de Départ ( GD) ..
Ce qui se traduit par l’égalité mathématique suivante :
(1)
NG =
(100 / 100) GD + (a / 100)
GD
si l ’on pose NG =
y ;
GD = x ; on remplace dans la relation (1) :
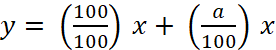
ce qui donne en factorisant :
|
|
|
|
Nous
remarquons que les deux termes 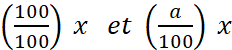 du second membre contiennent
comme « facteur commun » : «  »
|
|
|
|
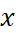si problème SOS cours : Factoriser 
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
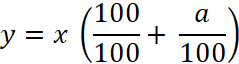
A
savoir :
|
|
|
|
en regroupant les termes dans la parenthèse ,
on obtient :
|
|
|
|
|
|
|
|
|
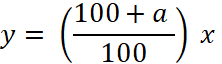
Traitement
mathématique de l’équation :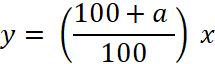 
|
|
|
|
( on appellera « traitement » les
transformations possibles de l’égalité en vue de trouver
« y » ; « a » ou « x ». )
Il faut se souvenir que :
« y » est l’ensemble
d’arrivée ; ( en économie on dira que c’est le
prix à payer après augmentation ).
« a » est la valeur
de l’échantillon pour cent de
l’ensemble de départ.
« x » est de
l’ensemble de départ (en économie ce
serait le prix que l’on payerait avant (ou sans) augmentation.
|
|
|
|
Premier calcul : rechercher la valeur après
augmentation :
|
|
|
|
|
|
|
|
On utilise l’égalité :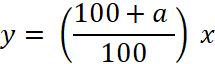
|
|
|
|
On
conclut que « le prix à payer après augmentation » est de :
|
|
|
|
|
|
|
|
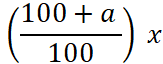
Application :
Un objet est à vendre à 1200
€ hors taxe ,la
taxe est de 25%. Quelle somme payerez vous ?
Résolution
Calcul direct :
1°) on pose :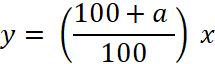
2°) on identifie : « y »= ? ; « x » = 1200 € ;
« a » = 25
3°)on remplace dans (1) :
y = ( (100+ 25 ) /10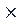0 ) 1200
€
4°) Calculs :
( (100
+25 ) /100 )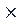1200
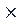F = (( 125)/ 100) )1200
€
= 1,25 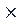1200
€
= 1500 €
5°) Conclusion : le prix à payer après l ’
augmentation de 25 % est de 1500 €
|
|
|
|
On peut trouver le résultat par une autre méthode :
1° )On calcule la
valeur de la remise avec la relation y
= ( a /100) x
2°) On pose : prix à payer = prix affiché + la taxe (en € .)
|
|
|
|
Deuxième type de calcul : On recherche le prix avant augmentation :
|
|
|
|
|
|
|
|
Soit
l’égalité :
|
|
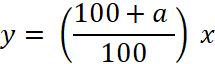
( on
recherche )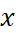
|
|
|
|
Nous obtenons après transformation:
|
|
|
|
|
|
|
|
|
|
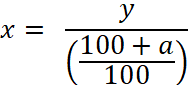
On conclut que « la somme »
affichée avant réduction était »
de :
|
|
|
|
|
|
|
|
|
|
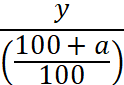
Application :
Un Objet est vendu toutes taxes comprises
1500 € ( de
25 %) quel était son hors taxe ( H.T.) ?
Résolution :
1°) On pose la relation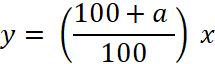
2°) On identifie : « y » = 1500
€ (prix à payer après réduction)
« a » = 25 ; « » = ?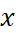
3°) On remplace dans (1) :
1500
€ = (( 100 + 25 ) /
100 )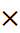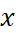 
4°)
Calculs :
1500 € =
(125 /100)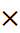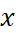
1500 € =
1,25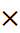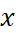
1500 € / 1,25
= 
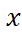
1 200 € =
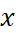
5°) Conclusion :
Le prix
avant augmentation (
dit aussi « hors taxe » ou noté H.T.
) était de 1 200 €
|
|
|
|
Il n’y a pas d ’autres méthodes !
|
|
|
|
Troisième
type de calcul :
rechercher le taux % d’augmentation :
|
|
|
|
soit l’égalité :
|
|
|
|
|
|
|
|
|
|
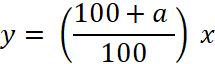
nous
obtenons : après transformation successive :
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
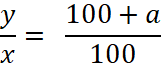
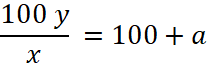
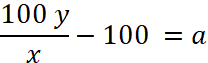
On conclut que « le taux de
l’augmentation » est de : = (100 y / x) - 100
|
|
|
|
Application : Un Objet est vendu 1500 € après
« augmentation » ;Son prix avant augmentation était de 1200 € . Quelle est le pourcentage
de l’ augmentation ?
Résolution :
1°) On pose la relation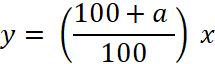
2°) On identifie : « y » = 1500 € (prix à payer après augmentation)
« a » = ? ;
« x » = 1200 €
3°) On remplace dans (1) :
1500 €
= (( 100 +a ) / 100 ) 1200 €
4°) Calculs :
1500 € / 1200 €
= (100 +a ) /100)
1,25 =
(100 +a ) / 100
1,25 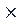100 =
100 + a
125 =
100 + a
125-100 =
a
a = 125 - 100
a = 25
5° ) Conclusion :
si « a » = 25 ; alors « a% » = 25 %
Le taux de l ’
augmentation est de 25 %
Autre
méthode :
On calcule la valeur de l ’ augmentation en « euros »
1500 € - 1200 €
= 300 €
On pose : y = (a / 100) 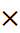 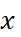; avec
« y » = 300 € ;
« a » = ? ; « »
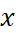= 1200 €
(voir objectif
« a% »)
Ce qui donne : « a % »= 25 %
|
|
|
|
|
|
|
|
|
|
|
|
