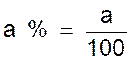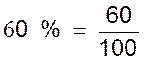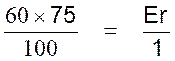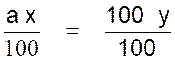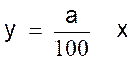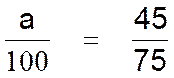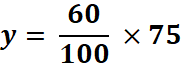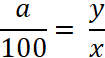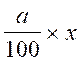|
DOSSIER : FONCTIONS LINEAIRES / Pourcentages / Objectif cours 45 |
Pré requis
|
Fractions équivalentes (égalité de
deux fractions ) |
|
|
Multiplication de deux fractions |
|
|
Multiplication d'une fraction par un nombre |
|
|
A propos de "a%" (notions) |
|
Objectif précédent : |
Objectif suivant : |
Et sommaire
|
|
|
Le POURCENTAGE :
a% |
|
|
|
|
|
|
|
Avant propos : « Le pourcentage » et « donnée statistique ». |
|
|
|
|
|
|
|
Traduction littérale de
« a% » |
|
|
|
Signification et explication concernant l '
écriture : (exemple )
représentation graphique et calcul avec 60 % |
|
|
|
I ) DETERMINATION D ’
UN POURCENTAGE, (« a % ») |
|
|
|
II ) Problème appelé :
POURCENTAGE DIRECT. |
|
|
|
III ) Problème
appelé : POURCENTAGE INDIRECT |
|
|
|
|
|
|
TEST |
COURS |
3°) Les égalités et les pourcentage |
Rappel : on appelle « grandeur » tout
nombre associé à une unité de mesure.
Définition
de l’objectif : tout savoir
sur une donnée statistique exprimée en
« a % »
(Pourcentage)
|
|
|
|
|
|
« Le pourcentage » et « donnée statistique » |
|
|
|
« a % » : Cette
écriture est utilisée en « statistique » « a » est une partie
d’un « échantillon » de 100
"éléments" ou « individus » C’est un coefficient: On l’appelle dans certains domaines: « taux » :
Exemples : « taux
d’intérêt d’emprunt » , « taux d’imposition sur les
revenus », « taux de cotisation à la caisse de retraite» ;
« taux de remise » , « taux de majoration » ....... Traduction littérale de
« a% » :
« a » est un nombre entier
; « a % » lire « a » « pour cent ». Exemple :60
% : lire soixante pour cent.
« a % » s ’ écrit sous
forme de fraction
de numérateur égal à « a » et de dénominateur égal à « 100 » : Important:
La fraction 60 /100
c’est aussi le nombre décimal : 0,60 . Signification et explication concernant l '
écriture : 60 % ;
Cette écriture est une donnée
« statistique » . Par exemple : 60 % d’élèves
de l’établissement ont obtenu leur CAP Ebéniste ,(
cela est une donnée statistique. ) *commentaire : On ne connaît pas
le nombre d’élèves reçus , ni le nombre d’élèves qui ont passé ce CAP. On peut simplement
dire que sur 100 élèves qui auraient passé cet examen « 60 » de ces
élèves (qui ont passés ce CAP) l’ont obtenu. Ce que l’on peut affirmer : 60% est égal au nombre d’élèves
reçus (noté « Er » ) sur le nombre
d’élèves candidats ( Ec )à l’obtention
du CAP ce qui peut se traduire en mathématique :
Exemple : Si 60 % des
élèves ont obtenu le CAP ,
combien d’élèves ont été reçus au CAP
sachant qu’ils étaient 75
candidats ? Procédure de
résolution : 1°) On pose
la relation (1
) Les élèves candidats sont
« les éléments de l ‘ ensemble de
départ » ( noté : Ec) ; Les
élèves reçus sont « les
éléments de l ‘ ensemble d ‘arrivée » ; noté Er 2°) On identifie : « a » = 60 ; E r
est ce que l’on cherche
(éléments de l’ensemble d’arrivée) ; E c
= 75 (éléments de l’ensemble de départ
) 3°) On remplace dans (1)
4°) Transformation et
calcul : Nous pouvons calculer la
quatrième proportionnelle : Soit 60 fois 75 = 4 500
et 4 500 : 100 = 45
; donc 45 = E r 5°) Conclusion : 45 élèves ont
été reçus à l’examen CAP d’ébéniste |
|
|
|
|
|
|
|
Représentation graphique des 60 pour
cent : par
un « camembert » |
|
50% 10% 40%
![]()
![]()
![]()
 Représentation graphique
des 60 %
Représentation graphique
des 60 %



![]() ( 50 %+10% )
( 50 %+10% )
|
|
|
|
||
|
|
On retiendra : · « a% » est une donnée
statistique qui se met sous la forme d’une fraction qui s ‘ écrit : a / 100 ou la fraction : · « Prendre le « a % »
« d’un nombre » (ou d’une
grandeur) , c’est rechercher par le calcul , la
valeur numérique d’une partie de ce nombre
( ou grandeur), représenté par
ce « a %. » · Le
pourcentage est une "application
" de la fonction linéaire ; le
« a% » est le coefficient de proportionnalité de la fonction
linéaire. Et appliqué à la fonction linéaire cela
donne : |
|
||
|
|
Par transformation
mathématique : (produit en
croix : voir GP1 :grandeurs
proportionnelles) :
Calcul : Pour obtenir « y » ; on divise
les deux membres par 100 (Voir EG4 : Théorèmes sur les égalités)
En nous reportant au modèle mathématique ( y = ax )de la fonction
linéaire ; nous pouvons écrire que (appliqué au pourcentage) :
Remarque :ce modèle est celui couramment utilisé pour calculer ce
que représente « a% » d’une grandeur. Dans tous
les cas : ·« y » représente les éléments de
l’ensemble d’arrivée .(c’est une valeur numérique (
45 élèves reçus )qui représentera la
partie de la grandeur de départ (75 candidats à l’examen) ·« x » représente les éléments de
l’ensemble de départ. (C’est un nombre ou une grandeur qui représente
l’ensemble de la « population » sur lequel s ’ applique ce
pourcentage , (75 élèves candidats)) ·
« y » peut représenter
« une augmentation » : on lui donnera le nom de
« taxe » ; « majoration » ,
un « agio » ; ou « y » peut représenter
« une
diminution » : on
lui donnera le nom de « remise » ,de
« rabais » ; un escompte….. ;
· résoudre un problème sur les pourcentages
c’est savoir, en fonction de l’ énoncé ,
surmonter 3 difficultés suivant
le cas: - chercher
« a » -
chercher « y » -
chercher « x » . |
|
||
|
|
|
|||
|
|
Rechercher ce que représente en pourcentage la partie d’une
grandeur donnée: « a »
Pour donner la réponse sous la forme de « a% » ,il suffit de calculer « a ». soit la
relation : exemple : Que représente en pourcentage 45 élèves reçus sur 75 ? Procédure : pour le calcul de « a » 1°) on
pose : 2° ) on identifie « y » = 45
(ensemble d’arrivée) ; « x »= 75
(ensemble de départ) 3°) on
remplace dans la relation :
4°) On
calcul (produit en croix) « a » = 100 fois 45 / 75 « a » = 4500
/ 75 « a » = 60 5°)
Conclusion : si
« a » = 60 ; alors
« a% » =
60% ; On a donc 60% d’élèves reçus à l’examen. |
|
||
|
|
II ) Problème appelé :
POURCENTAGE DIRECT |
|
||
|
|
|
|
||
|
|
Calcul de « y » ou
Rechercher ce que représente ; en nombre ; le « a% » d’un nombre ou d’une grandeur : |
|
||
|
|
Soit la relation : |
|
||
|
|
Exercice : 75 élèves se sont
présentés au CAP d’ébéniste ;on nous dit que
60% des élèves sont reçus. Quel est le
nombre de « reçus » ? |
|
||
|
|
Procédure
de résolution : calcul de « y » 1° ) On énonce
que : 2° ) On
identifie : « a » = 60
; « x »= 75 ( éléments de l’ensemble de départ
) ; « y »= éléments e l’ensemble d’arrivée. 3° ) On remplace
dans la relation (1)
4°) Calcul : ( voir
Obj , : QIII multiplication d’une fraction par un nombre) cela donne a) on transforme : b) on transforme :
c) opération : 4500 / 100 = 45 5°)
Rendre compte (conclusion) :
Il y a 45 élèves reçus sur 75 |
|
||
|
|
III ) Problème
appelé : POURCENTAGE INDIRECT |
|
||
|
|
|
|
||
|
|
Objectif : Calcul
de « x »
ou Rechercher le nombre de départ « x » qui a permis d’obtenir le nombre d’arrivée « y » en
fonction de « a% » . Exercice :45 élèves ont été reçu a l’examen
.Ils représentent 60% des élèves qui
se sont présentés à cet examen. Quel était le nombre d’élèves candidat a cet examen ? Procédure : Calcul
de « x » 1° ) On pose : 2° ) On identifie : « a » = 60 ;
« x » = ensemble de départ
; « y » = 45 3° ) On remplace dans (1) 4°) Calcul : (produit en
croix) x
60
x = 4 500 (voir
EG4 :transformation d’égalités ) x =
4 500 / 60 x = 75 5°)
Conclusion : 75 élèves étaient candidats à l’examen du CAP ébéniste , (dont 45
ont été reçus ;cela représentant
60% des candidats ) |
|
||
|
|
Pour chaque cas : Ne pas oublier de vérifier |
|
||
|
|
|
|
|
|
TRAVAUX AUTO – FORMATIFS. |
|
|
|
|
|
|
|
|
|
|
|
1°) Traduire en langage littérale : « a% » « 10% » On dit que a% est une
donnée : qu’est ce que cela signifie ? 2°) Traduire sous forme
mathématique : « a% » ; « 60% » 3°) Le pourcentage est une
application de la fonction linéaire ,justifier. ! 4°) Soit l’écriture :
y =
que représente ou
signifie chaque partie de cette
égalité ? « y » , « a
/100 » , « x » 5°) Soit l’égalité mathématique : Transformer cette
égalité : a = ? y = ? x = ? |
|
|
|
|
|
|
|
|
|
|
|
CONSIGNES : Pour chaque
exercice ou problème vous devez pour rendre compte indiquer les étapes
successives de votre démarche : 1° ) Donner l’équation mathématique . 2° ) Identifier les éléments : « a » = ; « y » = ;
« x » = 3°) Remplacer dans la relation (1) 4°) Faire les transformations et ou calcul 5° Rendre compte Niveau I 1. Calculer 3% de 100. 2. Calculer
18.6% de 320. 3. Calculer
110% de 400. 4. Prendre
3,7% de 100 Niveau II : 1. )
30 est une partie de 120 ; quel
pourcentage de 120 représente 30 ? 2. )
25 est une partie de 100 ; quel pourcentage de 25
représente 100 ? 3. )
25 éléments représentent 25 % d ‘un ensemble d’éléments
, combien contient d’éléments
cet ensemble ? 4. ) 30
éléments représentent 30% d ‘un ensemble d’éléments
, combien contient d’éléments
cet ensemble ? Calculer ce que représente en « a% » ; 30 par rapport
à 150. Niveau III : 1° ) 30 éléments représentent une partie
d’un ensemble qui en contient 100 ; quel est en pourcentage, ce que 30 représente par rapport
à l’ensemble « 100 ». 2° )
28 éléments représentent une partie d’un ensemble qui en contient 112; quel
est en pourcentage, ce que 28 représente par rapport à l’ensemble
« 112 ». |
|
|
|
|
|
|
|
|
|
|
|
|
|