NIVEAU  5 

Géométrie :  DOSSIER : PERIMETRE- AIRE - VOLUME /  Objectif cours 12c

Les unités de longueur

Index  warmaths

Objectif précédent   Périmètre « présentation »

Objectif suivant :

Périmètre de figures simples

·      Les cal culs d’aire  

·      Les polygones

·      2°) Présentation

  DOSSIER : PERIMETRES  (généralités)

Calcul du  PERIMETRE D’UN POLYGONE IRREGULIER.

I )  Définition de « périmètre » :

II ) Exemple  de calcul du périmètre d’un polygone quelconque (irrégulier).

III ) FORMULAIRE .

COURS.

I )  Définition de « périmètre » :

On appelle "périmètre" la longueur du contour d'une surface plane

Une longueur est une grandeur.

Le résultat  est donc un nombre associé à une unité extraite du tableau de conversion de longueur du système métrique.

Pour toute  figure géométrique : la longueur du périmètre est égale à la somme des longueurs des cotés formant la figure

(On a établi des formules pour calculer la longueur du périmètre  du carré , du rectangle , du parallélogramme , du trapèze , du triangle , du losange ,).Il est bon de les connaître par cœur ,ou de savoir les retrouver .

II ) Exemple  de calcul du périmètre d’un polygone quelconque (irrégulier) :

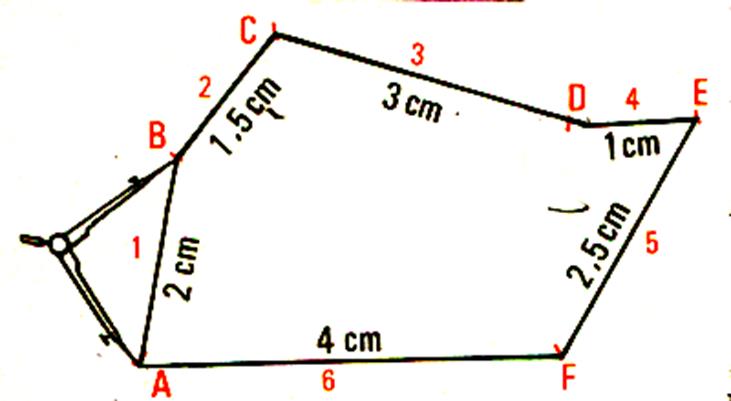
Le trait qui détermine cette figure est une ligne brisée fermée ;

Dans la figure ci-contre , cette ligne est formée de 6 segments de droite.

On développe  le contour de la figure , pour obtenir une ligne :

                                       Mesurons cette ligne brisée :Pour cela , il suffit de porter bout à bout les différents segments ( avec le compas ; par exemple )

Mesurer la ligne fermée qui limite une figure , c’est calculer le périmètre de la figure dessinée .

Cas particuliers :

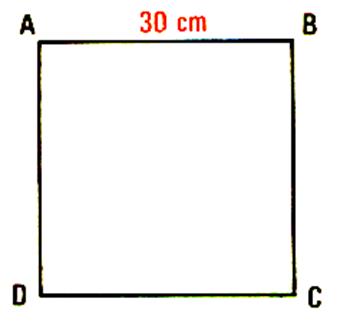
Pour le carré  : le périmètre est égal à 4 fois la longueur du segment AB ;

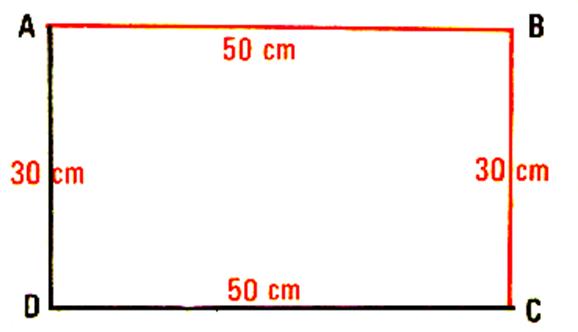
Pour le rectangle : le périmètre est égal la somme des longueurs des segments .

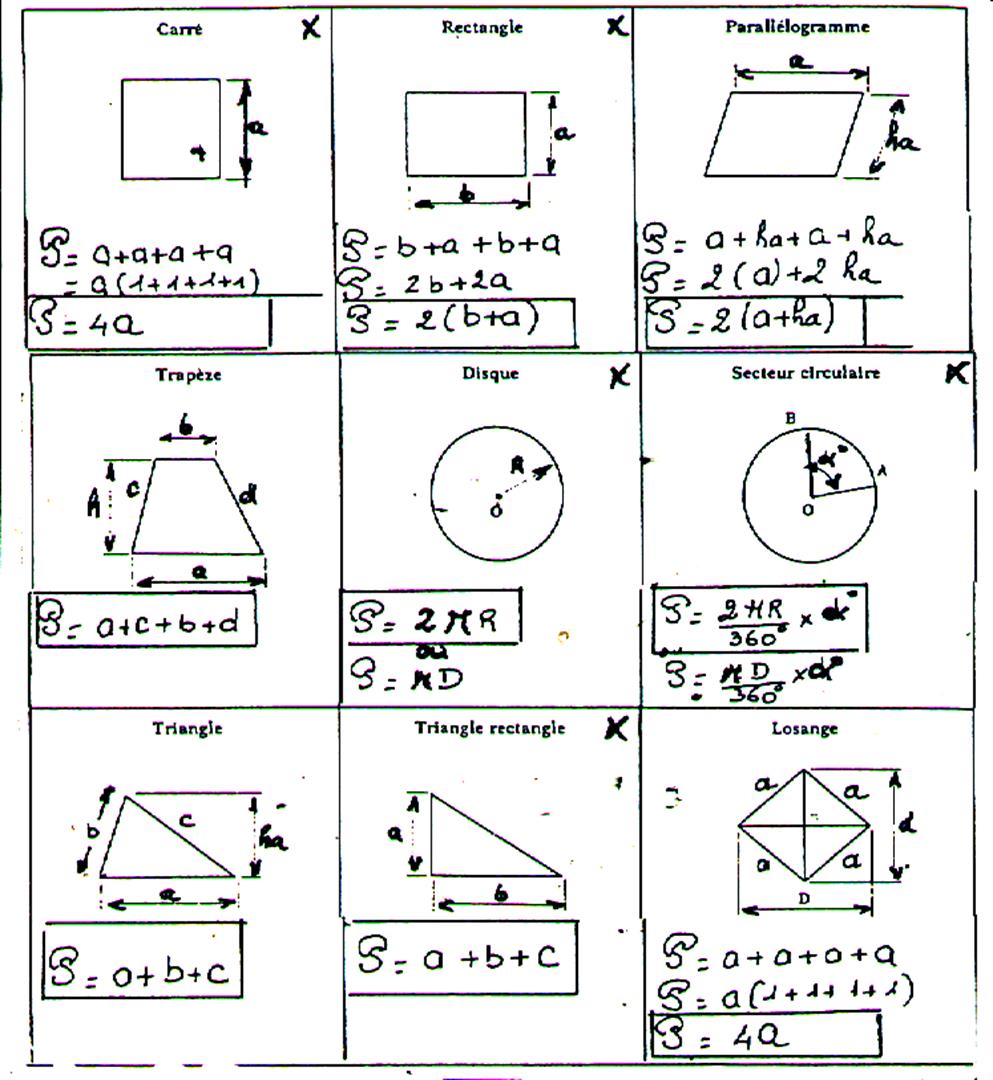
III ) FORMULAIRE :

Les cases marquées d’une croix sont celles dont le contenu est à retenir

                                     NOTA : Pour la plupart de ces figures , il a été établi des "formules" ; certaines sont à retenir parce que souvent utilisées.  (voir tableau )

TRAVAUX AUTO FORMATIFS :

CONTROLE :

1)   définissez la définition de « Périmètre » ?

EVALUATION :

Cliquez ici : Devoir niveau Contrôle  Continu

Pour chaque surface :compléter le tableau ;  donner la formule ; pour chaque exercice vous remplacez  les lettres par les valeurs données ; vous montrez le calcul.

Carré :

Rectangle :

Cercle :

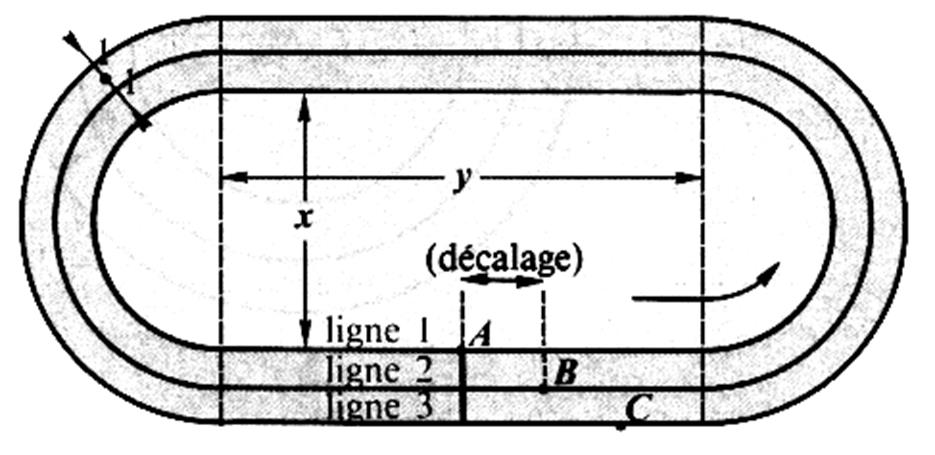
Problème :   « Les tours de piste »

Une piste d'athlétisme  possède 4 couloirs , un couloir par coureur.

Dans le dessin ci- dessus les couloirs ne sont pas dessinés ,les lignes représentent le milieu  ( l'axe) de chaque couloir.

1°) Exprimer en fonction de "x" et "y"  la longueur du tour de piste 1.

2°) Exprimer en fonction de "x" et "y"  la longueur du tour de piste 2.

3°) Exprimer en fonction de "x" et "y"  la longueur du tour de piste 3.

4°) Si l'on veut  que le coureur  "B" ligne 2  , parcourt  la même distance que le coureur "A" ligne 1 , il faut un "décalage" entre les coureurs "A" et "B" (voir figure)

Calculer ce décalage .  Dépend- il de "x" ? ; de "y" ?

5°) Montrer que le décalage entre les coureurs  A et B et le même qu'entre les coureurs "B" et "C" .