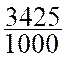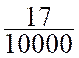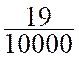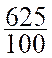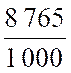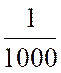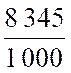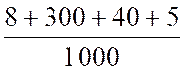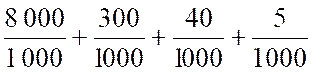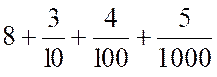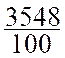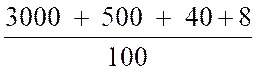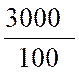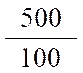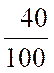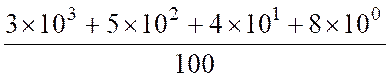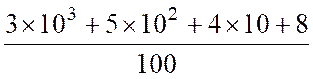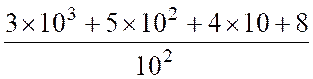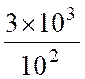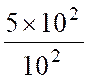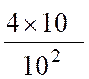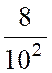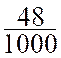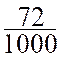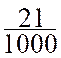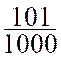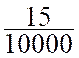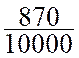Objectifs de cette leçon :

Objectif 1: Ecrire une fraction décimale sous forme de nombre décimal :

Objectif  2 : Ecrire un nombre décimal sous forme de fraction décimale .

Objectif 3 : Faire la différence entre : une fraction décimal et une fraction rationnelle.

I )  LA FRACTION DECIMALE

Rappel : un nombre décimal est un alignement horizontal de chiffre (s) séparé ou non par une virgule.  ( 0, 5    ;     1   ;   1,25  sont des nombres décimaux . Les nombres  sont toujours séparés par des points virgules. ( Info plus sur les conventions !!!)

COURS

1°)   approche  : 

On a vu qu’une fraction décimale du mètre  est une ou plusieurs parties de l’unité du mètre divisée (s)  en 10 ; 100 ; 1000.

Généralisons :

            Une fraction décimale est une ou plusieurs parties de l’unité divisée (s)  en 10 ; 100 ; 1000.

Une fraction décimale  peut s’écrire sous deux formes :

1°)par convention :  sous forme dite « nombre décimal » : exemple  0 , 35

2°) sous forme de fraction « ordinaire » : exemple : 

Pour écrire une fraction décimale sous forme de nombre décimal , on écrit  le numérateur  , à la droite duquel on sépare , par une virgule , autant  de chiffres décimaux qu’il y a de zéros au dénominateur .

Exemples :

   s’ écrit   3 , 425

     s’écrit 0,0017

Vu en primaire :  Pour écrire un nombre décimal sous forme de fraction décimale , on supprime la virgule , on prend pour numérateur de la fraction le nombre ainsi obtenu , et pour dénominateur l’unité suivie d’autant de éros qu’il y a de chiffres décimaux dans le nombre décimal donné .       

Exemples :

0,0019    s’ écrit    

6,25     s’ écrit   

2°)  Définition :

On appelle « fraction décimale » une fraction dont le dénominateur est une puissance de « 10 » , c'est-à-dire « 10 » ; « 100 » ; « 1 000 » ; «  10 000 » ; etc….

La fraction décimale «  » est une unité décimale du premier ordre ou  « dixième »

La fraction décimale «  » est une unité décimale du second  ordre ou  « centième »

La fraction décimale «  » est une unité décimale du troisième  ordre ou  « millième »

On voit que :

Dix unités décimales d’un ordre quelconque égalent l’unité décimale de l’ordre immédiatement supérieur.

3°)  Fraction décimale et nombre décimal »

Soit  la fraction décimale :  , on a    =  

Que l’on peut écrire  =

On convient d’écrire la fraction décimale sous la forme d’un nombre décimal :  =  8 , 345

Dans cette convention : Tout chiffre placé à gauche d’un autre représente des unités de l’ordre immédiatement supérieur.

Donc :

Pour obtenir le nombre décimal égal à une fraction décimale donnée on sépare par une virgule , à la droite du numérateur , autant de chiffres qu’il y a de zéros au dénominateur ;

Réciproquement le nombre décimal « 8,345 » est égal à la fraction décimale . Et par suite :

La fraction décimale égale à un nombre décimal donné est une fraction dont le numérateur est le nombre entier obtenu en supprimant la virgule et dont le dénominateur est l’unité suivie d’autant de zéros qu’il y a de chiffres décimaux après la virgule dans le nombre donné.

Exemple :  =  0,5

Remarque :    Un nombre rationnel représenté par une fraction décimale peut s’écrire sous forme de nombre décimal :

Exemple :  a =

  Solution 1 : 

                             a =   =   =    + +  + 

          ainsi

                               a = 30  + 5  +  + 

Solution 2 :  en utilisant les puissances de dix :

 a =   =   =      =

   a =    +   +  + 

   a  =   310     + 5       +      +   

ou  

    a  =   30    +   5    +   4 10^-1   +  8 10^-2

avec «  la convention de la virgule » entre le chiffre des unités et le terme en 10^-1  , on obtient l’écriture commode :   a =   35 , 48

Objectif 3 : Conversion d’une fraction ordinaire en nombre décimal en valeur exacte ou « approchée.  ( voir « arrondir à tant prés »)

Définition :

Convertir une fraction « ordinaire » en nombre décimal ; c’est chercher un nombre égal a la fraction ordinaire  ou qui en diffère de moins de 1 dixième , de 1 centième , etc .

Soit convertir    et   en nombre décimal. et

 =   0, 4375    à 0, 0001 près . ;  =  0,2727  environ ;

Règle :

Pour convertir une fraction ordinaire en nombre décimal on divise le numérateur par le dénominateur .

Si l’opération donne pour reste 0 , la conversion est exacte et le quotient décimal trouvé est égal à la fraction ordinaire . ( =  0,5)

Si l’on ne peut obtenir pour reste 0 , ou si l’on arrête la division avant d’obtenir pour reste 0 , la conversion n’est qu’approchée et le quotient décimal diffère  de la fraction de 1 dixième ; de 1 centième ;de  1 millième , etc. …..

(voir ci-dessous)

II ) FRACTION  représentée   par un nombre  dit : « RATIONNEL »

Voir  La « fraction périodique »  et   « fraction rationnelle»

La fraction « périodique » n’est pas une fraction décimale .

C’est ainsi 

Conversion approchée :  ( pour en savoir plus : voir l’ensemble des nombres rationnels)

Lorsque la conversion exacte est impossible  , on aperçoit au quotient décimal un ou plusieurs chiffres qui se produisent constamment dans le même ordre .

Ainsi en divisant 3 par 11 , nous trouvons  le quotient décimal 0 , 27272727..

On dit que 0,27272727…  est un nombre  décimal périodique  et que 27 est la période ;

On appelle : « période » la série  des chiffres qui se reproduisent sans cesse ;

    Le  nombre  représentant une fraction décimale périodique  est une « conversion approchée » .

Activité : On peut donner  deux énoncés  pour obtenir  une réponse équivalente.

1°) Calculer  « 3 : 7 »  ( que constate – t- on ? )

2°) Donnez la valeur décimale de la fraction :  .  Questions : peut-on donnez la valeur décimale «  NON » ; alors on donnera une valeur approchée…

((tests :info sur la division)

Calcul de la division de «  3 : 7 » :  =  0 , 42 8 57 1 42……….

Vous constatez que cette division ne se termine pas. (expliquez oralement pourquoi).

  ne peut pas s’écrire sous forme de nombre à virgule car il aurait une infinité de chiffres après la virgule.

Réponse : «  3 : 7   =  0 , 42 8 57 1 42………(n’a pas de fin) . »

Mais on continue d’écrire que le quotient de « 3 » par « 7 » est .

 n’est pas un nombre décimal.  ( on lui donnera le nom de « rationnel »)

3

0

7

2

0

0,42857142

6

0

4

0

5

0

1

0

3

0

2

0

6