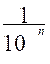MATHEMATIQUES - FORMATION COLLEGE :

Retour vers le sommaire Classe 4^ème de collège en mathématiques.	Vous êtes sur warmaths.fr	Collège: 4^ème
Ce qui suit est écrit par l’Education Nationale.
>>>Retour index warmaths .		Vers les listes des cours de collège..

	Ø Liste d’explication des contenus et compétences.
	EXPLICITATION DES CONTENUS DE LA CLASSE DE 4^e Il est rappelé que le professeur a toute liberté dans l’organisation de son enseignement à condition que soient atteints les objectifs visés par le programme
Les compétences concernent :
	1°) TRAVAUX GEOMETRIQUES	2°) TRAVAUX NUMERIQUES	3° ) GESTION DE DONNEES , FONCTIONS.

A ) TRAVAUX GEOMETRIQUES

En classe , de 4^e , la représentation d’objets géométriques usuels du plan et de l’espace , le calcul de grandeurs attachées à des objets , demeurent des objectifs majeurs ; s’y ajoute la caractérisation de certains d’entre eux .

Dans le plan , les travaux portent sur les figures usuelles déjà étudiées ( triangle , cercle , quadrilatères particuliers ) , mais également sur une nouvelle configuration illustrant une situation fondamentale de proportionnalité : celle de triangles déterminés par deux droites parallèles coupant deux sécantes. A ce nouvel outil et à ceux des classes antérieurs s’ajoute le théorème de Pythagore et la translation. Ces enrichissements doivent favoriser le développement des capacités de découvertes et de démonstration.

Dans l’espace , les travaux sur les solides étudiés exploitent largement les résultats de géométrie plane.

Contenus	Compétences exigibles . (voir la liste des fiches pédagogiques )	Commentaires
1. Triangle
Milieux et parallèles	Connaître et utiliser les théorèmes suivants relatifs aux milieux de deux côtés d’un triangle . Dans un triangle , si une droite passe par les milieux de deux côtés , elle est parallèle au troisième . Dans un triangle , si une droite passe par le milieu d’un côté et est parallèle à un second côté , elle coupe le troisième en son milieu. Dans un triangle , la longueur du segment joignant les milieux de deux côtés est égale à la moitié de celle du troisième côté.	La symétrie centrale et les propriétés caractéristiques du parallélogramme permettent de démontrer ces théorèmes.
Triangles déterminés par deux droites parallèles coupant deux sécantes.	Connaître et utiliser la proportionnalité des longueurs pour les côtés des deux triangles déterminés par deux droites parallèles coupant deux sécantes : Dans un triangle ABC , si M est un point du côté [AB] , N un point du côté [AC] et si [MN] est parallèle à [BC] , alors : = =	L’égalité des trois rapports sera admises après d’éventuelles études dans des cas particuliers. Elle s’étend bien sûr au cas où M et N appartiennent respectivement aux demi-droites [ AB ) et [ AC ) , mais on n’ examinera pas le cas où les demi-droites [ AM ) et [ AB ) , de même que les demi- droites [ AN ) et [ AC ) , sont opposées . Le théorème de Thalès dans toute sa généralité ainsi que sa réciproque seront étudiés en classe de 3^e .
Droites remarquables d’un triangle	Construire les bissectrices , les hauteurs , les médianes , les médiatrices , en connaître une définition et savoir qu’elles sont concourantes.	Certaines de ces propriétés de concours pourront être démontrées ; ce sera l’occasion de mettre en œuvre les connaissances de la classe ou celles de 5^e . On pourra étudier la position du point de concours de la médiane sur chacune d’elles.

Contenus	Compétences exigibles	Commentaires
2 Triangle rectangle et cercle .
Cercle circonscrit , théorème de Pythagore et sa réciproque	Caractériser le triangle rectangle : Par son inscription dans un demi-cercle Par la propriété de Pythagore et sa réciproque. Calculer la longueur d’un côté d’un triangle rectangle à partir de celles des deux autres . En donner , s’il y a lieu , une valeur approchée , en faisant éventuellement usage de la touche « racine : » d’une calculatrice . Caractériser les points du cercle de diamètre donné par la propriété de l’angle droit .	On poursuit le travail sur la caractérisation des figures en veillant à toujours la formuler à l’aide d’énoncés séparés. Les relations métriques dans le triangle rectangle , autres que celles mentionnées dans les compétences exigibles , ne sont pas au programme .
La droite « tangente » ; distance d’un point à une droite.	Construire la tangente à un cercle en l’un de ces points . Savoir que le point d’une droite le plus proche d’un point donné est le pied de sa perpendiculaire menée du point à la droite.	Le problème d’intersection d’un cercle et d’une droite fera l’objet d’activités ,sans pour autant que l’énoncé du résultat général soit une compétence exigible . L’inégalité triangulaire et la symétrie axiale , vue en classe de 5^e , permettent de démontrer le résultat relatif à la distance d’un point à une droite , lequel peut aussi être relié au théorème de Pythagore.
Cosinus d’un angle aigu	Utiliser , pour un triangle rectangle , la relation entre le cosinus d’un angle aigu et les longueurs des deux côtés adjacents . Utiliser la calculatrice pour déterminer une valeur approchée : -du cosinus d’un angle aigu donné . - de l’angle aigu dont on donne la cosinus.	La propriété de proportionnalité des côtés de deux triangles déterminés par deux parallèles coupant deux sécantes permet de définir le cosinus comme un rapport de longueurs . On peut également le définir comme l’abscisse d’un point sur le quart de cercle trigonométrique situé dans le premier quadrant .
	Voir une table numérique pour vérifier…..

Contenus	Compétences exigibles	Commentaires
3. Translation	Etant donné deux point A et B , sachant qu’une translation transforme A en b , construire : - l’image d’un point , appartenant ou non à la droite AB, -l’image d’un segment , d’une droite , d’une demi- droite , d’un cercle.l	Les vecteurs seront abordés en 3^e et leur étude sera reliée à celle des translations à l’occasion de la composition de ces dernières . Divers approches expérimentale , par exemple sur des frises ou des pavage , pourront introduire la notion de translation . La translation est définie à partir du parallélogramme . Elle pourra donner lieu à des manipulations , notamment sur des quadrillages .On pourra ainsi , après un travail ex ? conduisant à mettre en évidence la conservation des longueurs , de l’alignement , des angles et … ? justifier certaines de ces conservations

Contenus	Compétences exigibles	Commentaires
4. Pyramide et cône de révolution.	Calculer le volume d’une pyramide et d’un cône de révolution à l’aide de la formule : V = Bh/3	L’objectif est toujours d’apprendre à voir dans l’espace et de calculer des longueurs , des aires ,et des volumes , ce qui implique un large usage ? ? ? ? présentation en perspective et la fabrication de patrons . Ces travaux permettant de construire des images mentales relatives à des situations de parallélisme et d’orthogonalité . Activités :Tracer un cube en perspective. Sur la face supérieure trouver le centre de gravité (G) . tracer des droites issues des points de la base et joignant le centre (G) . Montrer la pyramide . Nommer les sommets par des lettres , nommer les arêtes qui joignent la base au sommet.

2°) TRAVAUX NUMERIQUES

la résolution de problèmes ( issus de la géométrie , de la gestion de données , des autres disciplines , de la vie courante ) constitue l’objectif fondamental de cette partie du programme . Elle nourrit les activités , tant dans le domaine numérique que dans le domaine littéral . Les exercices technique pure ne sont pas à privilégier .

La pratique du calcul exact ou approché sous différentes formes complémentaires ( calcul mental , calcul à la main , calcul à la machine ou avec un ordinateur ) a pour objectifs :

-la maîtrise des règles opératoires de base ,

-l’acquisition de savoir-faire dans la comparaison des nombres ,

-la réflexion et l’initiative dans le choix de l’écriture appropriée nombre selon la situation .

Le calcul littéral sera introduit avec prudence en veillant à ce que les élèves puissent donner du sens aux activités entreprises dans ce ca ? ? ? en particulier lors de l’utilisation de formules issues des sciences et de la technologie .

Contenus	Compétences exigibles	Commentaires
1-Nombres et calcul numérique
Opérations ( + ; - ;  ; : ) sur les nombres relatifs en écriture décimale ou fractionnaire ( non nécessairement simplifiée…)	Calculer le produit de nombres relatifs simples dans les différents cas de signe qui peuvent se présenter.	Toute étude théorique des propriétés des opérations est exclue. Les élèves ont la pratique de l’utilisation de la multiplication des nombres positifs en écriture fractionnaire . En s’appuyant sur ces connaissances , les opérations seront étendues aux cas des nombres relatifs. Les justifications pourront être portée à l’observation de l’extension de tables de multiplication ou à la généralisation de règles provenant de l’addition de nombres ( par exemple 3(-2) = -2 + -2 + -2 = -6 ;en admettant les résultats dans les autres cas.
	Savoir que =	Un travail sera conduit sur la notion d’inverse d’un nombre non nul , les notations x ^– 1 ou et l’usage de calculatrices avec la touche correspondante. A cette occasion, on remarquera que diviser par un nombre non nul , c’est multiplier par son inverse.
	Déterminer une valeur approchée du quotient de deux nombres décimaux ( positifs ou négatifs)
	Utiliser sur des exemples numériques les égalités : Cas 1 =  ; Cas 2 =  ; Cas 3  : = Où « a » ; « b » ; « c » et « d » sont des nombres décimaux relatifs.

	Calculer la somme de nombre relatifs en écriture fractionnaire.	L’addition de deux nombres relatifs en écriture fractionnaire peut demander un travail sur la recherche de multiples communs à deux ou plusieurs nombres entiers. La recherche du plus petit commun multiple pour l’obtention d’un dénominateur commun et celle du plus grand diviseur commun pour l’obtention de la forme irréductible ne sont pas exigibles .
Puissances d’exposant entier relatif	Utiliser sur des exemples numériques , avec ou sans calculatrice scientifique , les égalités : Cas 1 : 10^m + 10 ^n = 10 ^m+n ; Cas 2 : = 10 ^–n cas 3 : (10 ^m)^n = 10^mn où « m » et « n » sont des entiers relatifs.	En liaison avec la physique , les activités insisteront sur l’usage des puissances de dix . les calculatrices seront largement utilisées . Les élèves doivent maîtriser l’usage des touches correspondantes de leur calculatrice.

Contenus	Compétences exigibles	Commentaires
Notation scientifique des nombres décimaux . Ordre de grandeur d’un résultat.( ? )	Sur des exemples numériques , écrire un nombre décimal sous différente formes faisant intervenir des puissances de 10 . Utiliser la notation scientifique pour obtenir un encadrement ou un ordre de grandeur .	Modifier l’écriture d’un nombre comme 25 698,236 sous la forme 2,5698236 10^4 Ou 2569823,6 10^-2 ou 25,698236 10^3 est une activité que doivent pratiquer les élèves. La notation ingénieur n’est pas exigible .
	Utiliser sur des exemples numériques , pour des exposants très simples des égalités telles que : Cas 1 :a^2 a ^3 = a^5 Cas 2 : = a ^–3 Cas 3 : ( ab) ^2 = a^2 b^2 Où « a » et « b » sont des nombres relatifs non nuls .	Cette rubrique ne doit pas donner lieu à des calculs artificiels sur les puissances entières d’un nombre relatif. Pour des nombres autres que 10 , on s’en tiendra au cas d’exposants simples .
	Sur des exemples numériques , écrire en utilisant correctement les parenthèses , des programmes de calcul portant sur des sommes ou des produits de nombres relatifs. Organiser et effectuer à la main ou à la calculatrice les séquences de calcul correspondantes .	A la suite du travail commencé en 5^e avec des nombres décimaux positifs , les élèves seront entraînés aux mêmes types de calculs avec des nombres relatifs. Ils seront ainsi progressivement familiarisés à l’usage des priorités opératoires intervenant dans les conventions usuelles d’écritures ainsi qu’à la gestion d’un programme de calcul utilisant des parenthèses .

Contenus	Compétences exigibles	Commentaires
Touche de la calculatrice	Trouver à l’aide de la calculatrice une valeur approchée de la racine carrée d’un nombre positif. (comparaison avec une table )	Le théorème de Pythagore fournit l’occasion de calculer des racines carrées de nombres positifs dans des cas qui relèvent d’une situation où le nombre calculé a une signification que l’élève peut identifier. On peut aussi rattacher le calcul d’une racine carrée à des problèmes où interviennent l’aire d’un carré et la mesure de son côté.

Contenus	Compétences exigibles	Commentaires
Calcul littéral .	Réduire une expression littérale à une variable , du type : 3x – ( 4x – 2 ) ; 2x^2 - 3x + x ^2 ;	L’apprentissage du calcul littéral doit être fait très progressivement en recherchant des s ? ? ? qui permettent aux élèves de donner du sens à l’introduction de ce type de calcul .le travail proposé s’articule sur deux axes ?  -Utilisation d’expressions littérales pour ? ? numériques -Utilisation du calcul littéral dans la mise en équation et la résolution de problèmes divers. Les situations proposées aux élèves doivent ? ? tout type de virtuosité et répondre chaque …objectif précis ( résolution d’une équation ; ; ; ; ; ;d’un calcul numérique) . On évitera en ; ; ; ; ; expressions à plusieurs variables introduite.
Développement	Sur des exemples numériques ou littéraux , développer une expression du type ( a + b ) ( c + d) . Calculer la valeur d’une expression littérale en donnant aux variables des valeurs numériques .	Les activités de développement poursui ? ? ? ? ? de 5^e en utilisant l’identité k( a + b) = ka + kb . L’introduction progressive des lettres et des nombres relatifs s’intégrant aux expressions algorithmiques représente une difficulté importante qui doit ; ; ; ; en compte. A cette occasion , le test d’une ; ; ; ; substitution de valeurs numériques aux lettres : : : prendra tout son intérêt. Le développement de certaines expressions ( a+ b ) ( c + d) peut conduire à des simplifications d’écriture , mais les identités remarquables ne sont pas au programme . L’objectif est d’apprendre les élèves à développer pas à pas ce type d’expression en une somme de termes . La factorisation d’expressions analogue à X( 3x + 4 ) – 5 ( 3x +4) n’est pas au programme .t
Effet de l’addition et de la multiplication sur l’ordre . Application.	Comparer deux nombres relatifs simples en écriture décimale ou fractionnaire. Utiliser le fait que des nombres relatifs de la forme a +b et a +c sont rangés dans le même ordre que b et c . Utiliser le fait que des nombres relatifs de la forme « a c » et « ab » sont rangés dans le même ordre que b et c si « a » est strictement positif. Ecrire des encadrements résultant de la troncature ou de l’arrondi à un rang donné d’un nombre positif en écriture décimale ou provenant de l’affichage d’un résultat sur une calculatrice ( quotient , racine carrée , …..)	A partir d’une interprétation graphique , on ; ; ; ; ; le critère relatif au signe de la différence . Aucune connaissance n’est exigibles lorsque ; ; ;négatif , mais ce cas sera évoqué pour m ; ; ; nécessité de la condition a > 0 dans l’énonce ; ; ; ;propriété envisagée.
Résolution de problèmes conduisant à des équations du premier degré à une inconnue.	Mettre en équation et résoudre un problème conduisant à une équation du premier degré à une inconnue .	Les problèmes issus d’autres parties du programme conduisent à l’introduction d’équations et à leur résolution. On dégagera chaque fois sur ; ; ;problèmes particuliers les différentes étapes du ; ; ;mise en équation , résolution ; ; ; ;interprétation du résultat. Tous les problèmes aboutissant à des é ; ; ; ; ; ; produits du type (x-2) ( 2x – 3 ) = 0 ; s ; ; ; ; ; ;programme

3° GESTION DE DONNEES , FONCTIONS

Les notions essentielles relatives à cette rubrique ont été introduites ou approfondies en classe de 6e et classe de 5e . En 4^e ces notions seront fréquemment réinvesties dans les mêmes conditions que celle explicitées dans le programme de 5^e , avec une insistance particulière sur l’utilisation des moyens de calcul moderne.

Le lien entre les autres disciplines et avec l’éducation à la citoyenneté sera maintenu et renforcé. Comme en 5^e , le mot « fonction » sera employé , chaque fois que nécessaire , en situation , et sans qu’une définition formelle soit donnée.

Contenus	Compétences exigibles	Commentaires
1 représentation graphique . Proportionnalité	Utiliser , dans le plan muni d’un repère , la caractérisation de la proportionnalité sous forme d’alignement de points avec l’origine .	On fera travailler les élèves à la fois sur des exemples et des contre-exemples de situations de proportionnalité .
2 . Applications de la proportionnalité
Vitesse moyenne Grandeurs quotients courantes	Utiliser l’égalité d = v t pour des calculs de distance parcourue , de vitesse et de temps . Changer d’unités de vitesse ( mètre par seconde et kilomètre par heure ) d’autres exemples….	Les situations où interviennent des vitesses moyennes constituent des exemples riches où le traitement mathématique s’avère particulièrement pertinent , comme l’étude de la vitesse moyenne d’un trajet sur un parcours de 60 km , où l’aller se parcourt à 20 km.h^-1 et le retour à 30 km.h^-1 ;Les compétences exigibles se réduisent aux vitesses mais d’autres situations de changement d’unités méritent d’être envisagées : problèmes de change monétaire , consommation de carburant d’un véhicule en litres pour 100 km ou en kilomètres parcourus par litre .
Calculs faisant intervenir des pourcentages		En liaison avec d’autre discipline ( géographie,…) la notion d’indice pourra être présentée comme un cas particulier du coefficient de proportionnalité , donnant lieu à illustrations et calculs mais en aucun cas à des développements théoriques.

Contenus	Compétences exigibles	Commentaires
	Mettre en œuvre la proportionnalité dans des situations simples utilisant à la fois des pourcentages et des quantités ou des effectifs .	Des situations issues de la vie courante ou des autres disciplines demandent de mettre en œuvre à la fois un coefficient de proportionnalité , sous forme de pourcentage ou d’indice , et des quantités ou des effectifs . par exemple , connaissant le pourcentage d’un caractère dans deux groupes d’effectifs différents , déterminer le pourcentage obtenu après réunion des deux groupes .

Contenus	Compétences exigibles	Commentaires
3.Statistiques
Effectifs cumulés , fréquences cumulées . .	Calculer des effectifs cumulés ; des fréquences cumulées .
Moyennes pondérées	.calculer la moyenne d’une série statistique . Calculer une valeur approchée de la moyenne d’une série statistique regroupée en classes d’intervalles	L’élève sera confronté à des situations courantes où la méthode de calcul est à remettre en cause ; par exemple , les différences constatées entre la moyenne annuelle des notes d’un élève calculée à partir de l’ensemble des notes de l’année ou à partir de la moyenne des moyennes trimestrielles.
Initiation à l’utilisation de tableurs – grapheurs .		Les tableurs – grapheurs , utilisés dès la 5^e en technologie , introduisent une nouvelle manière de désigner une variable :par l’emplacement de la cellule où elle se trouve dans un tableau . Cette nouveauté est un enrichissement pour des utilisations dont on pourra donner des exemples . Pour les graphiques des choix successifs sont proposés , ils conduisent naturellement à examiner leur pertinence pour l’illustration d’une situation donnée.