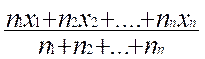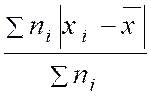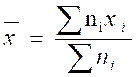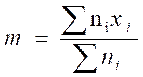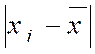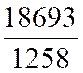Pré requis:

Les Statistiques  info
« Somme »

ENVIRONNEMENT du dossier:

 

Index : warmaths	Objectif précédent  1°) la moyenne arithmétique (non pondérée).	Objectif suivant  1°) les moyennes arithmétiques pondérées par …...	1°) Tout sur les calculs de  moyennes . 2°) Liste des cours de statistiques

DOSSIER : « La MOYENNE ARITHMETIQUE PONDEREE appliquée aux notes pondérées.» et

 « L’ ECART MOYEN ARITHMETIQUE »

 

	I )  Calculs de la moyenne arithmétique pondérées.  =    ou       =             Application  au calcul de moyenne avec notes coefficientées.
	II )  Calcul de l’ écart moyen arithmétique.     E )   =

 

 

 

TEST

COURS

Devoir  Contrôle

Devoir évaluation

Interdisciplinarité

Corrigé Contrôle

Corrigé évaluation

 

 

COURS N°

 

Activité :

MOYENNE PONDEREE ( associée à des notes coefficientées)

 

Notes coefficientées :

Dans le système éducatif , des matières enseignées ont plus « d’importance » que d’autre. Une façon de tenir compte de cette importance c’est de donner un coefficient multiplicateur supérieur à 1 , est de multiplier la note importante par ce coefficient.

Exemple : pour un CAP on attribut à chaque matière un coefficient

 

 

Matière	Coefficients
Français	4
maths	4
Langue vivante	1
EPS	1
Enseignement professionnel	10

 

 

 

 

Soit un relevé de note de l’élève :

 

Matière	Coefficients	note
Français	4	12
maths	4	8
Langue vivante	1	5
EPS	1	14
Enseignement professionnel	10	12

 

 

 

Calculs des notes coefficientées

 

Matière	Coefficients	note	notes coefficientées
Français	4	12	4 12 = 48
maths	4	8	4 8 = 32
Langue vivante	1	5	1  5 = 5
EPS	1	14	1   14 = 14
Enseignement professionnel	10	12	10   12 = 120

 

 Bilan : analyse

 

 

Matière	Coefficients	note	notes coefficientées
Français	4	12	4 12 =                48
maths	4	8	4 8 =                   32
Langue vivante	1	5	1  5 =                    5
EPS	1	14	1   14 =                 14
Enseignement professionnel	10	9,5	10   12 =              120
Total des coefficients : 4+4+1+1+10 = 20
Total des notes coefficientées :			219

 

 

Moyenne pondérée : 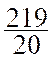  =  10,95   soit la note est de  10,95 / 20

 

Conclusion : la moyenne pondérée est égale à la somme des notes coefficientées divisée par la somme des coefficients

 

 

 

Généralisons :

Le calcul de la moyenne se résume à la formule :   =

 

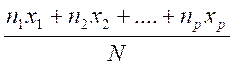
lorsque le caractère ( x :la note sur 20)  prend  "n₁" fois  ( le coefficient ) la valeur "x₁" ; "n₂" fois la valeur "x₂" , etc. et "N" le total des coefficients .

 

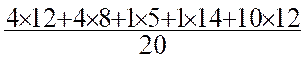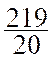  =  = = 10,95

 

Nous trouvons  une moyenne de 10,95   dans les deux calculs .

 

 

II ) Calcul de l’ écart moyen arithmétique. ( E )

Procédure (étapes de calculs)

1°) Calculer la moyenne de la série statistique.

Pour chaque valeur de la variable (valeur du caractère) ,on calcule la valeur absolue de l’écart par rapport à la moyenne.    que vous voyons écrit aussi :

2°)Calculer  les distances :   ;   ;  ;…………

3°) Multiplier chaque distance ;par l’effectif correspondant :

n1 =………   ; n2  =………………. ;  n3  =……. ; ……….. ; np

4°) Faire la somme des différents produits obtenus .

5°) Effectuer le  quotient  (diviser)  de la somme obtenue par l’effectif   total .   ( N  ) ; que l’on note aussi )

 

	Formule :
	E )   =
	Exemple :
		xi	ni	xi  -	ni
		165	150	-28,18	150 x 28,18 = 4 227
		175	190	- 18,18	3 454,2
		185	203	- 8,18	1 660,5
		195	270	+ 1,82	491,4
		205	190	+ 11,82	2 245,8
		215	150	+  21,82	3 273
		225	105	+  31,82	3 341,1
			1 258		18 693
	( E )=

 

 

 

TRAVAUX AUTO FORMATIFS.

CONTROLE :

 

                         1° ) Qu’est qu’une « moyenne » ?

2° )Donner le modèle mathématique. (équation)

3 ° )  Qu’ appelle –t-on « moyenne arithmétique pondérée » (donner la formule de calcul) ?

 

EVALUATION

 

1°)  Calculer la moyenne pondérée :

Matière	Coefficient	note	notes coefficientées
Français	4	12
maths	4	8
Langue vivante	1	5
EPS	1	14
Enseignement professionnel	10	9,5
Total des coefficients :
Total des notes coefficientées :

 

Moyenne pondérée : ?

 

2°)  Compléter le tableau ci-dessous et  Calculer l’écart moyen arithmétique
	xi	ni	xi  -	ni
	165	150
	175	190
	185	203
	195	270
	205	190
	215	150
	225	105
( E )=

 

Voir exercices «  arithmétique »

 

INTERDISCIPLINARITE

 

Domaine :  Trigonométrie  :

 

I )   Compléter  le tableau suivant :

A savoir :  15° < 15° 30’ < 16°

Avec la table Ldonnant des valeurs  au degré prés…

Alpha =	15°	16°
Sinus alpha =

 

Calcul de la moyenne :

Sinus 15° 30’

Sinus 15°  = sinus 0.2588

Sinus   16° = 0,2756

moyenne :(0,2588 +0,2756) :2 =  0,2672

 

 

 

corrigé CONTROLE :

 

                       1° ) Qu’est qu’une « moyenne » ?

2° )Donner le modèle mathématique.

3 ° )  Qu’ appelle –t-on « moyenne pondérée » (donner la formule de calcul) ?

 

corrigé EVALUATION

 

Calculer la moyenne pondérée :

Matière	Coefficient	note	notes coefficientées
Français	4	12
maths	4	8
Langue vivante	1	5
EPS	1	14
Enseignement professionnel	10	9,5
Total des coefficients :
Total des notes coefficientées :

 

Moyenne pondérée : ?

 

 

Voir exercices «  arithmétique »

 

corrigé INTERDISCIPLINARITE

 

Domaine :  Trigonométrie  :

 

I )   Compléter  le tableau suivant :

A savoir :  15° < 15° 30’ < 16°

Avec la table Ldonnant des valeurs  au degré prés…

Alpha =	15°	16°
Sinus alpha =

 

Calcul de la moyenne :

Sinus 15° 30’

Sinus 15°  = sinus 0.2588

Sinus   16° = 0,2756

moyenne :(0,2588 +0,2756) :2 =  0,2672