Auteur : WARME R.   revu le 26 1104         Dossier : PROFESSEUR.     d’un point à une droite D’un  point   à une droite. et d’un segment d’un angle. et
NOM : ………………………………	Prénom : …………………………..	Classe :…………………..
Année    scolaire : ………………………	Dossier pris le : ……/………/………	Validation de la  formation :    O -  N              Le : …………………………………….. Nom du  formateur  : ……………………
ETABLISSEMENT : …………………………………………..

 

 

 

DOC. INFO : Professeur ; Formateur

15/26

DOC : livre  Elève .. Vu : 17 / 10 /2003 A terminer.

Titre : DISTANCE  et MEDIATRICE  d'un segment  et BISSECTRICE d'un angle

DOSSIER  N°15 INTERACTIF DISTANCE  et MEDIATRICE  d'un segment  et BISSECTRICE d'un angle .

Information « TRAVAUX  d’auto - formation » Cliquer sur  le mot « travaux »!.

INFORMATIONS PEDAGOGIQUES :

NIVEAU : Formation  Niveau V  (inclus le CAP et CFA)

OBJECTIFS : - Savoir construire le projeté orthogonal d'un point sur une droite. - Savoir calculer ou  trouver graphiquement la mesure de la distance (longueur comprise) entre deux points  et d'un point à une droite. -          Savoir construire à la règle et au compas la médiatrice d'un segment donné. -          Savoir construire à la règle et au compas la bissectrice d'un angle donné .

I ) Pré requis:

Lectures importantes :	Cochez !!
Conventions d’ écriture  et de symbolisation utilisées en géométrie.. ( longueur ; distance ;….d’un segment)
Angle ( définition)	Ÿ
La direction  et le sens .	Ÿ
Les perpendiculaires	Ÿ
Longueur d'un segment.	Ÿ
Longueur , distance , mesure algébrique! ! ! ! !	Ÿ
La médiatrice	Ÿ

II ) ENVIRONNEMENT du dossier :

Index

Objectif précédent : 1°) Revoir : Mise à niveau 2°)La projection orthogonale d’un point sur une droite. 3°) Les unités d’ angles et ……

Objectif suivant : 1°) Les Symétries 2°) tracer des angles à 15° ; 30° , 45° ;….

1°)Tableau  2°) liste des leçons. 3°) résumé 3ème

III )  LECON  n° 15 : DISTANCE  et MEDIATRICE  d'un segment  et BISSECTRICE d'un angle .

Chapitres :

I ) Perpendiculaire menée d'un point sur une droite .	Info plus!!! Les tracés de perpendiculaires
II ) Distance d'un point à une droite .	Info plus 1 !! projection orthogonale! Info plus 2 !!!:longueur d'un segment.
III ) La hauteur	Info ++ sur la hauteur !!
IVI )Médiatrice d'un segment .	Info plus : la médiatrice
IV ) La bissectrice	Info plus !!! les bissectrices !
V)   La médiane	Info ++ sur la médiane.

IV)   INFORMATIONS  «  formation leçon » :

Test	COURS	Travaux  auto - formation.			Corrigé des travaux  auto - formation.
		Contrôle	évaluation	INTERDISCIPLINARITE	CORRIGE contrôle  :	CORRIGE  évaluation :
TRAVAUX niveau VI et V
« Perpendiculaire »		Dossier 5859
« Distance »		Dossier 5858 : Exercice « 8 »
« médiatrice »		Cours spécifique.
« hauteur » et  « bissectrice »		; Dossier 91

V )   DEVOIRS  ( écrits):

Devoir diagnostique L tests.	Ÿ
Devoir  Auto  - formatif  (intégré au cours)	Ÿ
Devoir Formatif  « Contrôle : savoir » ;   ( remédiation)	Ÿ
Devoir  Formatif  «  Evaluation   savoir faire »  ( remédiation)	Ÿ
Devoir sommatif .	Ÿ
Devoir certificatif : (remédiation )	Ÿ

* remédiation : ces documents peuvent être réutilisés ( tout ou partie) pour conclure une formation .

 

Leçon	Titre
N°15	PERPENDICULAIRE - DISTANCE  et MEDIATRICE d'un segment  et BISSECTRICE d'un angle .

CHAPITRES

I ) Perpendiculaire menée d'un point sur une droite .	Info plus!!! Les tracés de perpendiculaires
II ) Distance d'un point à une droite .	Info plus 1 !! projection orthogonale! Info plus 2 !!!:longueur d'un segment.
III ) La hauteur	Info ++ sur la hauteur !!
IVI )Médiatrice d'un segment .	Info plus : la médiatrice
IV ) La bissectrice	Info plus !!! les bissectrices !
V)   La médiane	Info ++ sur la médiane.

 

 

COURS

 

 

Pré requis 1: longueur d'un segment. On se contentera de la définition suivante :On appelle "longueur d’un segment " la dimension d'un morceau de droite   mesurée avec une règle graduée  ( la mesure se fait de  l’ une à l' autre de ses extrémités).

       (l'unité de longueur est le « mètre » ou un de ces multiples ou sous multiples)

 

 

Pré requis 2 : Projection orthogonale d’un point :

 

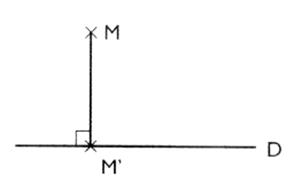
d   Par définition : Si  ( D) est perpendiculaire à "d" et si MM' est parallèle à "d" alors  M ' est le projeté orthogonal de M sur la droite ( D) .

 

Pré requis 1 :

I )PERPENDICULAIRE  menée d'un point sur une droite.

Info plus 1!!! tracés de perpendiculaires

Pré requis : i lire sur C d : la perpendiculaire.

Perpendiculaire :  par définition 

Deux droites sont perpendiculaires si elles forment un angle « droit ». ( = 90°  ou 100 gr.)

Exemple :

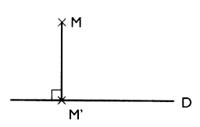
La droite  passant par  les points M M' est perpendiculaire à la droite    ( D) .  parce qu ’ : elles forment un angle droit Les 90 ° sont à  mesurer avec un rapporteur .

Le petit « carré » symbolise l’angle droit

Activité 1:

On demande : A l'aide d'une équerre ;

- Tracer une perpendiculaire à la droite (D) et passant par le point "M" . Cette droite coupe (D) au point M' .

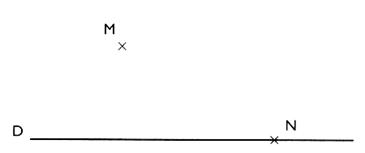
- Tracer une droite passant par N appartenant à ( D)

Le point M ’ doit se trouver sur   la droite  D

      On  dit que :       M ' est le projeté orthogonal  de M sur  ( D)

(info plus sur C d  !!sur le projeté  orthogonal d'une point )

 

i9

II ) DISTANCE D’UN POINT A UNE DROITE.

:iInfo plus 1 !! projection orthogonale!

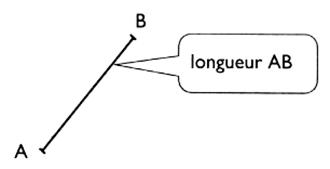
a)   Définition  de la « distance entre deux points » :  ( @ activité primaire)

par définition

On dira que la distance entre deux points est égale à la longueur d'un segment de droite ayant pour origine et extrémité ces deux points .

 

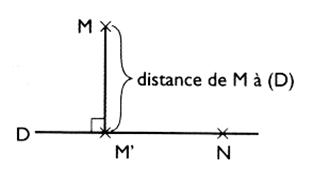
b) Définition  de la  « distance entre un point et une droite » :

 

par définition : La distance entre un point et une droite est celle que l'on mesure sur le segment de droite  porté par la projection orthogonale.

Cela induit que cette distance est la  longueur la plus courte qui existe entre le point M et sa projeté M'. Dans tous les cas :  long [MN] > long [MM']   Ce segment  MM’  a pour bornes ,le point extérieur à la droite et l'  "image"  de ce point située sur la droite .

 

iInfo : Ce « savoir » est à réutiliser et réinvestir   pour construire deux droites parallèles , et pour tracer une tangente à un cercle.

 

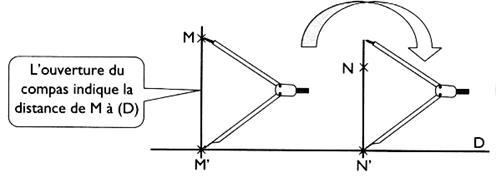
i Comparaison de  distances :

On compare les distances avec le compas : on remarque que  d( NN') < d ( MM')  Remarque  importante ! « On compare des distances » et « l'on mesure des longueurs. »!

La longueur qui détermine la distance  sera mesurée avec une  règle graduée .

 

Info plus !!! sur la hauteur.

III )   La HAUTEUR

:i   et @3ème

La hauteur est une droite tracée  perpendiculairement à une droite donnée , passant par un point  donnée.

 

Dans un  triangle ; la hauteur  est un segment de droite  qui joint un point perpendiculaire au côté opposé à ce point..

 

 

 

Info plus !!! sur la médiatrice.

IV  )  MEDIATRICE  D’UN SEGMENT .

:i

 

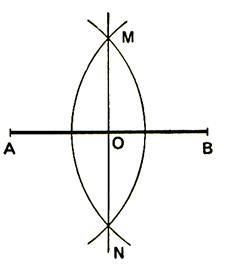
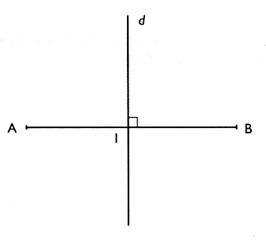
a) Définition :         La médiatrice d'un segment  est la droite perpendiculaire en son milieu .

 

Remarque : Chaque  point de la médiatrice est à égale  des extrémités du segment .

 

Exemple :  sur la figure ci dessous  la droite (d) est perpendiculaire au segment AB , cette droite coupe le segment en ( I ) milieu du [AB]  ; on en conclut que (d) est médiatrice du segment AB.

b) Construction d’un médiatrice :

Pour construire  la médiatrice  ( M N) d'un segment [AB] à la règle  et au compas , il faut donner au compas une ouverture supérieure à la demi- longueur AB .

iInfo : Applications cliquer ici : tracer les médiatrices d’un  triangle ;ou ,  recherche du centre d’un cercle ou disque .

 

Pré requis :  notions .

V ) BISSECTRICE d ‘ UN ANGLE .

Info Cd plus !sur la bissectrice!!!

a)      définition :

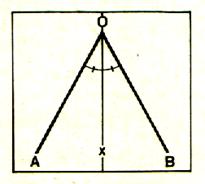
Une bissectrice   est  une 1/2 droite qui part du sommet d'un angle et qui coupe cet angle en deux parties égales.   Elle partage l'angle en deux angles de même mesure .

b) Construction de la bissectrice d'un angle:  ( Info C d  plus  sur les constructions!!!)

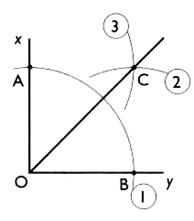
Soit un angle formé par les deux demi-droites : [O y) et  [O x) . 1°) Tracer un arc de cercle  de centre "O" coupant [O y)  en B et [O x)  en A. 2°) tracer un arc de cercle (2) de centre "B" . 3°) tracer un arc de cercle (3) de centre "A" . les deux arcs se coupant en C. 4°) tracer une droite d'origine "O" et passant par "C" .

 

Pré requis :  notions .	V I ) MEDIANE .		Info Cd plus !sur la médiane!!!
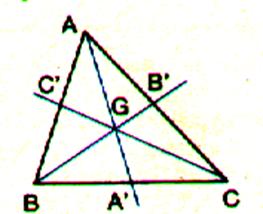
Définition : Une médiane  est une droite issue d’un  point (sommet d’un angle) et qui joint le milieu d’un segment.   Le point "G"  se trouve toujours au 2/3 de la longueur de la médiane en partant de chaque sommet. (ce qu'il faut démontrer !!!)   (ATTENTION : sur la figure ci-contre A', B' et C' ne sont pas exactement au milieu des segments).

 

 

Leçon	TRAVAUX d ’ AUTO - FORMATION sur
N°15	DISTANCE  et MEDIATRICE  d'un segment  et BISSECTRICE d'un angle .

 

 

°) Quand dit-on que deux droites sont perpendiculaires ?

 

2°) A quoi est égale la distance entre deux points ?

 

3°) Par définition : qu' appelle - t- on  « distance d'un point  à une droite » ? ;  Qu'est ce que cela implique ?

 

4°); Donner la définition d'une "médiatrice" .

 

5°) Donner la définition d’une  " bissectrice" ? 

 

6°) Donnez la définition de la « hauteur » .

 

7°) Donnez la définition de la  « médiane » .

 

Appliqué au  triangle.

 

8°) Qu ' est ce qu'une "médiatrice" ? ( précisez  le trait  est une droite , demi droite , segment  , en prenant comme figure géométrique le triangle )

 

9°) Qu'est ce qu'une " bissectrice" ? ( précisez  le trait  est une droite , demi droite , segment  , en prenant comme figure géométrique le triangle )

 

 

10°) Qu'est ce qu'une " hauteur " ? ( précisez  le trait  est une droite , demi droite , segment  , en prenant comme figure géométrique le triangle )

 

 

11°) Qu'est ce qu'une " médiane  " ? ( précisez  le trait  est une droite , demi droite , segment  , en prenant comme figure géométrique le triangle )

 

 

 

Série 1 :

 

A)  Projetée orthogonale

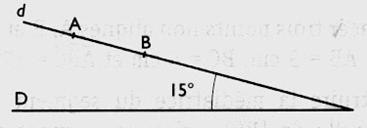
1°) Sur la droite "d" , les deux points  A et B sont distants de 5 cm .

 

Déterminer la longueur de       [ A' ; B ']  , projeté orthogonale sur  (D ) de [A B]

 

Même question avec des angles  de 30° ; 60 ° et 90°

( ce travail  sera exploité par   "Thalès"  et en trigonométrie "tangente")

 

2°) Projection orthogonale d'un segment sur une droite :

a)  Reproduire la figure . Construire A' et B'  , projetés orthogonaux de A et B  respectivement sur  ( D)  , et tracer [ A ' B' ]   : le segment [ A ' B' ] est le projeté orthogonal du segment [A B] .

b)      Placer  le point M , milieu de [A B]  et construire M' son projeté  orthogonal sur  ( D )  . Quelle est la position de M' sur [ A ' B' ]

 

Idem :

Idem :

B ) Distance :

1°) tracer une droite  ( D )  et placer un point  distant de 5 cm  de ( D)  .

 

2°) sur une carte au 1 / 100 000  on trouve quatre villes  A ; B ; C et D .

 

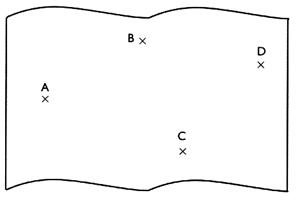
A l'aide  du compas seulement , classer les distances AB ; BC ; BD ; AC ; AD et CD dans l'ordre décroisant .

Médiatrice :

2°) Construire à la règle et au compas  la médiatrice   d'un segment de droite de 7,5 cm de longueur .

 

3°)Placer 3 points non alignés A , B et C tels que  : AB = 3 cm ; BC = 4 cm  et  = 120° .

Construire la médiatrice du segment AB puis celle du segment BC ; elles se coupent en un point  " I " .

Tracer le cercle de centre "I" et de rayon " I A " .

Que constate - t- on ? Justifier la réponse .

 

4°) On donne un point "B"  Construire une droite (d) dont la distance de "B" est de 2,5 cm.

Bissectrice .

Tracer la bissectrice de l'angle .

 

Série 2 :

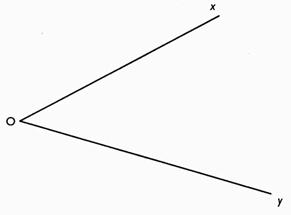
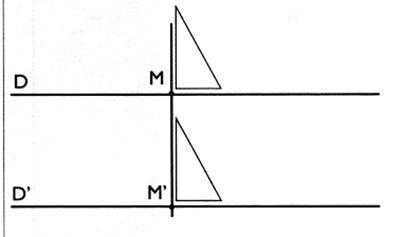
1°)  Distance  de deux droites parallèles :

On donne deux droites parallèles distinctes  ( D ) et ( D') . Placer un point "M" sur  ( D)  et tracer  la perpendiculaire à  ( D ' ) passant par M ;elle coupe  ( D ' ) en M'  ; M' étant le projeté orthogonal de M sur  ( D') . La distance de ( D) à ( D') est égale à la distance de  M à M' ( longueur du segment [ M M '] ; mesurer cette distance  et vérifier que :

-          le projeté orthogonal de M'  sur ( D) est le point M ;

-          la distance trouvée ne dépend pas du point M choisi .

 

2°) Construire  deux droites parallèles  situées à 5 cm l'une de l'autre .

pour cela :

-          Tracer une droite ( D).

-          Tracer une droite (d) perpendiculaire à ( D) qui coupe ( D) en  "H" . ( utiliser l'équerre)

-          Placer sur (d) le point "M"  situé à 5 cm de "H"  .   ( il y a deux solutions )

-          Tracer la droite ( D') perpendiculaire à ( d ) et passant par M . 

 

 

3°) Construire à la règle et au compas la médiatrice ( D) d'un segment AB de 6 cm de longueur  . Soit  "F"  le point d'intersection de ( D)  et de [ A B ] .

Placer  sur la médiatrice deux points  C et D situés de part et d'autre de  F tels que F  soit le milieu de [ C D ]  . Que représente la droite ( AB) pour le segment [ CD] . Quelle est la nature  du quadrilatère ACBD ?

 

4°) Placer trois points A , B et C  tels que  AB = 5 cm  , BC  = 6 cm , AC = 7 cm. Construire la médiatrice du segment [ AC] puis celle  du segment BC . Elles se coupent en O .

Tracer le cercle de centre "O" et de rayon OA . Les points B et C appartiennent - ils au cercle  ? Justifier la réponse .

Vérifier que la médiatrice  du segment AB passe par le point  I .