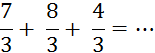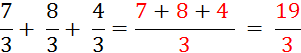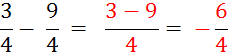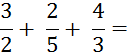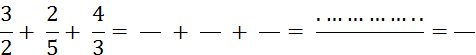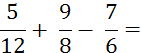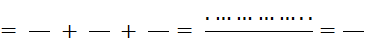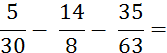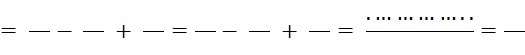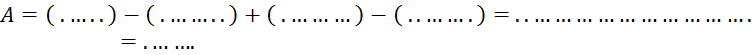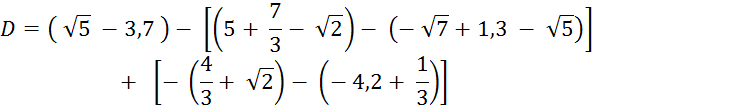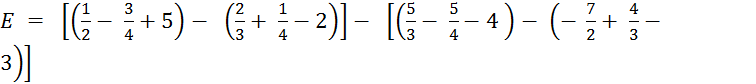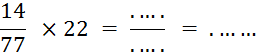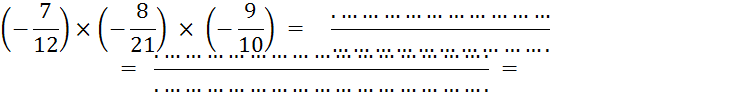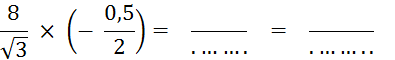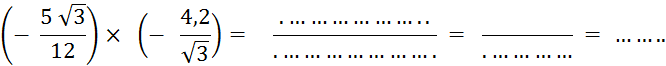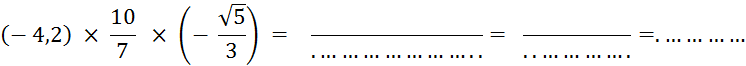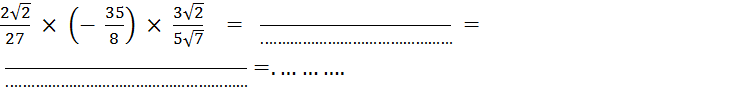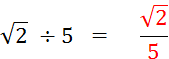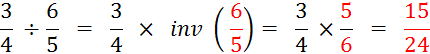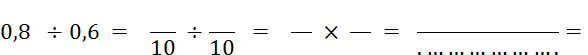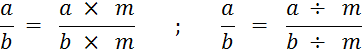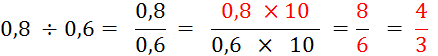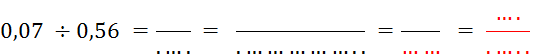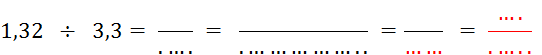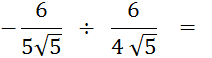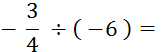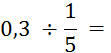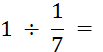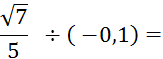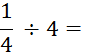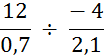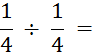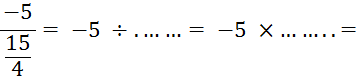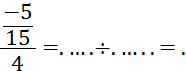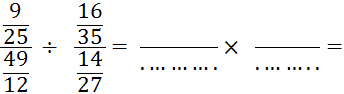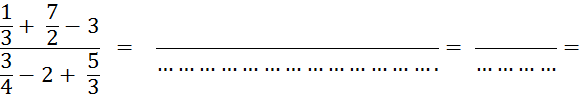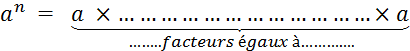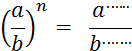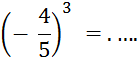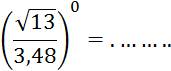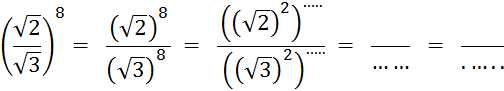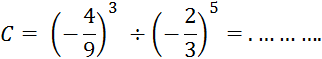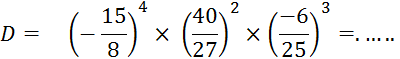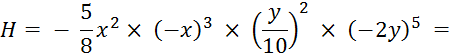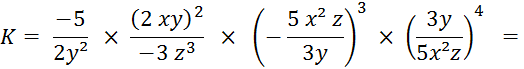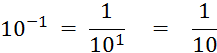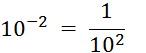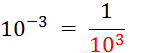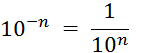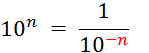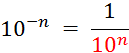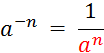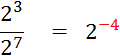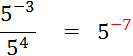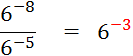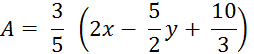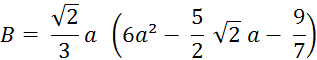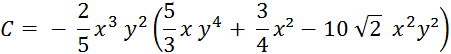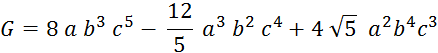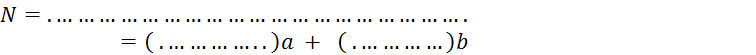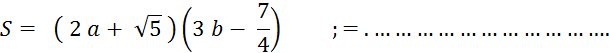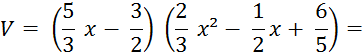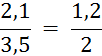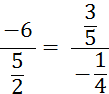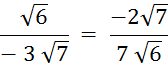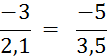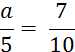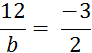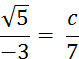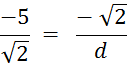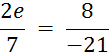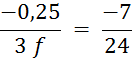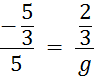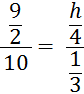Prérequis : Rappels essentiels

Fiche 1 : Addition – Soustraction.

Fiche 2 : Multiplication.

Fiche 3 : Division .

Fiche 4 : Puissances d’exposant positif.

Fiche 5 : Puissances dont l’exposant est un entier relatif.

Fiche 6 : Produit nul. ( et équation produit)

Fiche 7 : Distributivité de la multiplication sur l’addition .

Fiche 8 :  Proportions.

Fiche  9 : Proportionnalité – Pourcentage – Application Linéaire. ( à faire dans le même temps )

Fiches de travaux sur :

Fiche 1 : Addition - Soustraction

Info +++@ ++++

Rappelez verbalement  ( en expliquant @ ) les propriétés de l’addition.  ( commutativité , associativité , élément neutre ).

·       Tout nombre relatif «  » possède un opposé.  «  s’ écrit «  »  , «   »

Exemple :

Opp

Opp

Opp

Soustraction :

Info @ sur  …..soustrac

« » , «  » , « » étant des relatifs quelconques , «  » existe toujours.

«   »  signifie que  «   »   ;    «   »

Activité 1 : Calculez :

Info @

( - 1,25 )

Info @

Info @

Info @

Activité 2 :

1°) Calculez « A » en effectuant d’abord l’intérieur des parenthèses.

2°) Calculez «  » en supprimant d’abord les parenthèses.

Activité 3 :

Supprimez les parenthèses puis simplifiez l’écriture de «  » . ( «  » et «  » sont des nombres ).

Faites de même pour : 

Activité 4 :

Supprimez  les crochets  et parenthèses puis simplifiez l’écriture de « D ».

·       Faites de même pour 

Fiche 2 : Multiplication.

Info ++@ ….

Rappelez verbalement ( en expliquant ) les propriétés de la multiplication. ( commutativité ; associativité  , élément neutre ) …..

·       Tout nombre relatif non nul possède  un inverse .   s’écrit :       .   et    : 

Exemples :

«  inv ( 7 ) = …… »

«  inv ( -  ) = …( -  ) … »

«  inv (- ) = …(- 3 )… »

«  inv (  ) = …… »

«  inv (  ) = …… »

·        Pour tout nombre relatif « a » ,      ;

Dans un produit de facteurs si l’un des facteurs est nul , le produit est ..nul …..

Calculez :  

Convention d’écriture :

Info +++@ …

«  » et «  » étant des nombres relatifs :

«  »   s' écrit     «   »  

«  »   s' écrit     «   »  

«  »   s' écrit     «   »  

«  »   s' écrit     «   »  

«  » étant un nombre relatif ,

« » et «  »  étant des nombres relatifs,

«   »

 ( - 1 )

«  »

Activité 1 :

Calculez :   = 

Remarque :

Vous savez que « » étant un nombre positif ,    . C’est- à- dire :      

Complétez :      ;    

·       Calculez : 

Priorité de la multiplication sur l’addition .

Info +++@ …..

Activité 2 :

Calculez :  

·       Calculez : 

·       Calculez :         

Info :   Commencez par calculer      

·       Puis : :         

Enfin : :          

Fiche 3 : Division .

Info @ ++  sur la division…

«  » et «  » étant des nombres  relatifs , «   »

«    » s’appelle « quotient »  de  «  » par «  »

«    »

«    » signifie  que  «    » 

Activité 1 :

Exemple :

       en effet   

7   2  =     

Activité 2 :

Info ++@ ……

Calculez :

Calculez :

Propriété des quotients :

«  » , «  » , «  »  étant des nombres relatifs  «  » non nul , «  » non  nul ;

Activité 3 :

L’exercice précédent  peut alors se faire de la façon suivante :

Faîtes de même pour : 

Signification  de 

«  » et «  » étant des nombres relatifs 

 ,      ;              ;    

Sont des nombres égaux que l’on écrit 

Activité 4 :

Info ++@pour en savoir plus ……

Calculez : 

Activité 5 :

Calculez :

Fiche 4 : Puissances d’exposant positif.

Info + @ …………….

«  » étant un nombre relatif et «  » un entier , .

Par convention ,

Si   ; 

    se lit  «   » .       est la puissance de «  » d’exposant «  ».

Ø Les propriétés suivantes ont été démontrées en classe  précédente

Info +++@ ………

«  » et «  »  étant des nombres relatifs , «  » et « »  des entiers naturels, ( «  » et «  » non nuls si «  »  ou «  »

Activité 1

Calculez :

Activité 2 .

Mettez sous la forme de produits de puissances de « 2 » ; »3 » ; « 5 ».

Activité 3 .

Complétez le tableau :

« a »

2a

« a² »

2 a²

( 2 a )²

3a

( 3 a )²

3 a²

Activité 4 . Calculez .

Activité 5 . «  »   , «  » et «  » étant des nombres relatifs non nuls , simplifiez l’écriture de :

Fiche 5 : Puissances dont l’exposant est un entier relatif.

Info ++@ +++…….

Vous avez vu dans la classe de niveau inférieur que :

« n » étant un entier naturel :

Si       donc  ;   donc     

On peut donc dire :

«  » étant un entier relatif quelconque :

·       Ce qui est vrai pour « 10 » , l’est aussi pour tout nombre relatif non nul.

«  » étant un nombre relatif non nul et «  » un entier relatif.

Les formules sont les mêmes que dans le cas d’exposants positifs.

Activité 1 :

Complétez :

Info + @ ++ …..

Activité 2 :

Calculez « A »

Ecriture scientifique d’un nombre

Info ++ @ +++…..

L’écriture scientifique de « 5 740 000 »  est  «   »    .     Celle de     est 

Activité 3 :

Donnez l’écriture scientifique :

Activité 4 :

Calculez :

Fiche 6 : Produit nul.  ( et équation produit)

Info + @ …procédure (étapes) apprentissages et études …+++

info + »0 » et  sur l’élément absorbant

Dans un produit , si l’un des facteurs est nul, alors le produit est   nul.

Calculez :

                    Inversement :  «  » et «  » étant des nombres relatifs quelconques , sachant que :    , cherchons si l’un des facteurs «  » ou « » est nul .

Supposons que « a » ne soit pas nul . Il possède alors un inverse «  ».

Puisque    alors       ce qui s’écrit :      , or    , l’égalité s’écrit alors «  »  , c'est-à-dire  «   » 

En définitive : si : «   »    et «  »  alors «  » . On peut donc dire :

A retenir :

Si dans un produit , l’un des facteurs est nul alors le produit est nul.

Si un produit de facteurs est nul , alors l’un au moins des facteurs est nul.

«   »    signifie  que  «  »  ou  «  »

Application :

Résolvons l’équation    d’inconnue « »

Le premier membre de cette équation est un produit et de produit doit être  égal à 0.

D’après ce qui précède , ce produit ne peut être nul que si l’un des facteurs est  nul .

«   »    ou «  »   Les solutions de l’équation sont donc     et  .

Activité 1 :

Résolvez l’équation : 

Fiche 7 : Distributivité de la multiplication sur l’addition :

La multiplication est distributive sur l’addition se traduit par :

Pour tous nombres «  »  ,         ; 

Pour tous nombres «  »  ,         ;  

Activité 1 :

Attention :

Transformez en simplifiant :

Activité 2 :

Factorisez :

Activité 3 :

Réduisez les termes semblables de :

 ;    

 ;  

 ;      

Activité 4 :

                          Développez et réduisez :

    ;

Activité 5 :

Réduisez les termes semblables après avoir enlevé crochets et parenthèses.

Produit de sommes :

Pour tous nombres      

Pour tous nombres       

Activité 6 :

                          Développez et simplifiez :

Info : commencez par développer  , par exemple.

Suite :  

Fiche 8 :  Proportions.

Info + … Proportion……

Vous avez vu dans les classes de niveau inférieur  «  5^ème »  et « 4^ème » 

A retenir :

 sont des nombres , « » et «  » ne sont pas nuls ( dénominateurs)  dire que   c’est dire que «   »

Quatre nombres  dans cet ordre , « » et «  » non  nuls , tels que   constituent une « proportion ».

  sont des « extrêmes »     sont les « moyens ».

Dans toute proportion , le produit  des extrêmes est égal au produit des moyens.

Activité n° 1. :

Vérifiez ces égalités en calculant le produit des extrêmes et le produit des moyens.

. ……………………………………………………

. ……………………………………………………

. ……………………………………………………

. ……………………………………………………

Activité n° 2 :

« x » et « y » sont des nombres tels que  «  132 x = 84 y »  . Déterminez    ( simplifiez ) .

Activité n° 3 :

1° )   «  »  , dans cet ordre , constituent-ils une proportion ?

2°)  même question pour : «   »

Autre propriété :

La multiplication étant commutative, les égalités suivantes ont même signification.(  sont des nombres relatifs non nuls )

«    »

«    »

«    »

«    »

Donc , les égalités ci-dessous ont même signification.

A retenir @:

Dans l’ensemble des nombres relatifs non nuls , étant donné une proportion , si l’on échange les moyens ou si l’on échange les extrêmes , on obtient une nouvelle proportion.

Activité n° 4 :

Vérifiez l’égalité ci-dessous et écrivez trois autres égalités.

Activité n° 5 :

Vous allez résoudre l’équation :        , d’inconnue «  »

    signifie que          , c'est-à-dire que :       donc   :   ; 

Activités (suite) :

Résolvez au brouillon les équations ci-dessous et écrivez à côté la solution :

Fiche  9 : Proportionnalité – Pourcentage – Application Linéaire

Faites ces recherches au brouillon , n’écrivez sur ce document que les résultats.

Activité 1 :

Information :

Dans un magasin, on fait un rabais  de  15% sur les prix marqués.

Sachant que le prix marqué d’un objet est de 340 € ; la remise sera alors  de :

Le prix « à payer » , après remise sera : 340 € - 51 €  = 289 €  

Suite :

Désignons par « M » le prix marqué ( en €) et par « P » le prix payé  ( en € ),

La remise sera alors de  , c'est-à-dire  «  »

La prix  payé sera : «   »  qui s’écrit   «  » , c'est-à-dire «   »

Le procédé mathématique qui fait passer de «  »  à «  » est une application linéaire.

Activité 2 :

( info : taux de TVA à 19.6% pour la presse numérique)

Pour calculer le prix de vente taxes comprises ( TTC) , on ajoute au prix hors taxes ( HT) une taxe appelée « TVA ». ( il existe plusieurs taux de TVA )

Dire que le taux de TVA est de 19,6 % , c’est dire que la « TVA »  est les « 18,6 % du prix « HT ».

En définitive , ; c'est-à-dire  

Complétez le tableau :

Prix  HT

Taux TVA

Prix TTC

5480 €

33,3 %

19,6%

195,69 €

64 €

67,52 €

Activité 3 :

Une ville compte 19 000 habitants en 2019 . En admettant que la population augmente régulièrement de 3,4 % par an , quel sera le nombre d’habitants en un an ? ………

.

En quelle année la population aura-t-elle doublé ? …….

( utilisez convenablement votre calculatrice )

Activité 4 :

Une voiture consomme 6,25 litres d’essence aux 100 km.

En imaginant cette consommation « régulière » , c'est-à-dire proportionnelle au nombre de km parcourus, le procédé mathématique qui au nombre de km fait correspondre le nombre de litres est une application linéaire.

Quel est son coefficient ?.........................................

Avec cette voiture, combien de km peut-on parcourir avec 1 litre d’essence ?

Activité 5 :

En 2034 , le trafic aérien mondial a été de 1763 milliard de passagers-kilomètres.

Ce nombre est obtenu en totalisant le nombre de km parcourus par chacun des passagers.

1°) Si ce nombre correspondait au déplacement d’un seul passager, a combien de tours de terre correspondrait-il ? ( Tour de la terre environ 40 000 km )…………………………………………………………………………..

2°) Si ce nombre correspondait au déplacement de tous les habitants de la terre, ( 5 milliards d’habitants), combien chaque habitant aurait-il parcouru ? ………………………………………………………………………………

Activité 6 :

Dire qu’un appareil électrique a consommé « 1 kw h » , cela peut valoir dire