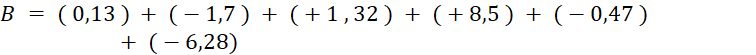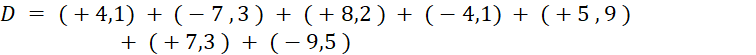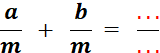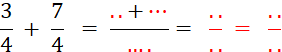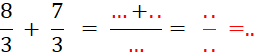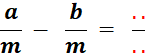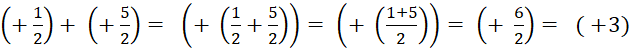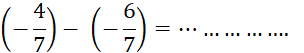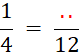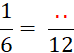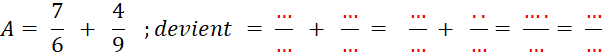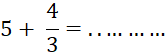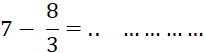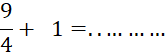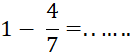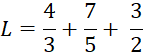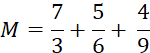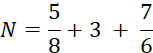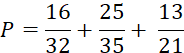Fiche 1 : Les nombres relatifs.

Fiche 2   Comparaison de nombres relatifs.

Fiche 3 : Addition de nombres relatifs.

Fiche 4 : Soustraction de nombres relatifs.

.

Fiche 5 : Somme ou différence  de nombre relatifs en écriture fractionnaire

Fiche 6 : Réduction au même dénominateur.

Fiche 7 : Activités  Exercices et situations problèmes.

Fiche 8 : Exploitation de données statistiques. (Activités complémentaires)

Fiche 1 : Les nombres relatifs.

Info ++ le nombre relatif

·       ( + 9 ) ; (  - 5 ) ; 0 ; ( - 64 ) sont des nombres dits : « entiers relatifs ».

·       ( + 9 ,1 ) ; (  - 5,06  ) ; 0 ; ( - 0, 64 ) sont des nombres dits : « décimaux  relatifs ».

·        9  ;  5  ; 0 ;  64  ;  9 ,1  ;  5,06 ; 0 ;  0, 64 : les valeurs numériques des nombres relatifs  (ci-dessus) sont appelées : « valeur absolue ».

Info +++ :

Ø « 5 »  peut s’écrire « 5,0 »  ou  « 5,000 » ou ……….

Ø « - 17 » peut s’écrire  «  - 17 , 00 »   ou   « - 17 , 0000 »  ou ……..

Ø Aussi  tout  entier relatif peut être considéré comme un  ………………..…..

Ø A partir d’un entier quelconque, ( « 7 » par exemple) on a obtenu 2 entiers relatifs.

7

   ( + 7 )

( + 7 ) peut s’écrire    7.

 ( + 7 ) et ( - 7 )  sont  « opposés »

 ( - 7 )

Ø A partir d’un entier quelconque, ( « 0,7 » par exemple) on a obtenu 2 décimaux relatifs.

0,7

   ( + 0,7 )

( + 0,7 ) peut s’écrire    0,7.

( + 0,7 ) et ( - 0,7 )  sont  « opposés »

 ( - 0,7 )

v Vous savez que  0,7 peut s’écrire :

Vous concevez alors que l’on puisse écrire  ( + 0,7 ) =     et    ( - 0,7 ) = .

A partir de     , on a obtenu  deux nombres relatifs :    et    .

v Dans le cas de        ( qui n’est pas un décimal) , on fera pareil.

Et on écrira par convention     =    

Et     et  sont des opposés.

 .

Fiche 2   Comparaison de nombres relatifs.

Info +++ : sur la comparaison…

La règle est la même que celle que vous avez étudiée en classe précédente ( 5^ème ) pour les décimaux relatifs.

Règle :

-        Tout nombre positif est supérieur ou égal à zéro.

-        Tout nombre négatif est ………………………… à zéro.

-        Tout nombre positif est   supérieur à tout nombre négatif.

-        Si deux nombres  sont rangés dans un certain ordre  leurs opposés  sont rangés dans l’ordre  « opposé ».

-        De deux nombres négatifs, le plus grand est celui des deux  qui a la plus petite valeur absolue.

Activité n°….1 :

Complétez en mettant le signe   ( >    ou     <  )

( - 19 ) ……( + 9 )

( - 22 )  ……. ( - 5 )

( + 0,07 ) ….( - 54 , 8 )

( - 1,287 ) ……( - 1,3 )

Activité n°…2 :

Rangé dans l’ordre croissant :

( - 0,19 )

( + 5,7 )

( - 4 , 83 )

( + 0,035 )

( - 4,7 )

( - 0,051)

( - 2 )

( + 5,4 )

( - 0,04 )

Activité n°…3 :

Comparez …

Vous en déduisez que 

Comparez : 

Fiche 3 : Addition de nombres relatifs

Info ++ sur l’addition de deux nombres relatifs.

Activité 1

Calculez :

( + 54 ) + ( - 27 ) = ……

( + 17 )   + ( + 25 ) = …..

( + 33 ) +  ( - 33 ) =…….

( - 15  ) + ( + 27 ) = ……

( + 9 ) + ( - 29 ) = ……

( 0 ) + ( +17 ) = ……

( - 47 ) + ( - 14 ) = ……

( - 5 ) + 0  = ……

( - 54 ) + ( + 27 ) = ……

( + 21,78 ) + ( - 49,37 ) = ……

( - 43,74 ) + ( + 18,543 ) = ……

( + 47,2 ) + ( + 13,57 ) = ……

( - 0,09 ) + ( - 0,051 ) = ……

( - 3, 54 ) + ( + 0,547 ) = ……

( + 43,52 ) + ( - 0,48 ) = ……

Les propriétés de l’addition.

Info +++sur

Ø L’addition des nombres relatifs est « commutative » , cela signifie :

« a » et « b » étant des nombres relatifs quelconques, «  a + b = …………… »

Ø L’addition des nombres relatifs est « associative  » , cela signifie :

« a », « b » et « c »  étant des nombres relatifs quelconques, «   »

On convient alors de ne pas mettre de parenthèses.

  peut s’écrire

De même :      peut s’écrire :

Ø « 0 » est élément neutre  pour l’addition  des nombres relatifs , signifie :

« a » étant un nombre relatif quelconque, «  a + 0  = . ..… »    ;   «  0 + a = …….... »

Ø Chaque nombre relatif possède un « opposé » (unique).

Info ++ sur l’opposé.

Activité 2 :

Opp. ( - 7,5 )  =  …………..

Opp. ( + 8,3 )  =  …………

Opp  =   ……

Activité 3 :

( + 5 ) + ( - 5 )  =   …….

( + 0,17 )  +  ( - 0 ,17 ) = ………..

« a »  étant un nombre relatif quelconque :

«  »

Opp   =  Opp.   =  

« a »  étant un nombre relatif quelconque :

Activité 4 :

Ø Calculez après avoir regroupé les positifs d’une part et les négatifs d’autre part.

Ø Faites de même pour « B ».

Activité 5 :

Calculez après avoir simplifié les opposés. (Vous soulignerez les termes opposés)

C = ( - 7 ) + ( - 4 ) + ( + 5 ) + ( + 7 ) + ( - 9 ) + ( - 5 ) + ( + 8 ) ;   

Faites de même pour  « D »

Activité 6 :

Calculez suivant la méthode demandée :

1°) Méthode : Effectuez d’abord le calcul dans les parenthèses.

2°) Méthode : Enlevez d’abord les parenthèses ( grâce à l’associativité) puis calculez « E ».

Faites de même pour « F » .

1^ère Méthode :

2^ème méthode :

Fiche 4 : Soustraction de nombres relatifs.

Info + sur la soustraction avec deux nombres relatifs.

Vous avez vu dans la classe précédente ( 5^ème) que :

Définition :

            «  » et «  » étant des nombres relatifs , on appelle « différence de «  » et «  »  le nombre relatif qu’il faut ajouter  à «  » pour obtenir … «  » …..

«   »     signifie que «  »

Règle :

La différence de deux nombres relatifs ( pris dans un ordre déterminé) est un nombre relatif qui existe toujours.

Pour le calculer , on ajoute au premier nombre l’  « ………… » du deuxième.

«  «  »

Activité n° …Calculez les différences suivantes en utilisant la règle.

( - 26 )  - ( + 33 )  =  …..…….+……….…..=  ……

( + 37 )  - ( - 69  )  =  ………….+……………..=  …………

( 0  )  - ( - 67  )  =  ………….+………...=  …………

( - 4,5  )  - ( + 0,7   )  =  ………….+……………..=  …………

( +0,12  )  - ( - 0,12  )  =  …  ….+….. .=  ………….

(- 7,49  )  - ( 0  )  =  ………….+……………..=  …………

( + 6,8  )  - ( - 4, 9   )  =    …….+……..=  ……

( + 84  )  - ( + 28   )  =  ………….+……………..=  …………

( - 57  )  - ( - 37  )  =  ……….+………..=  …………

( - 5,7)  - (  + 5,7  )  =  ………….+……………..=  …………

Ø Questions : la soustraction de nombres relatifs est-elle « commutative » ?  ……….  Est-elle « associative » ?...............

Fiche 5 : Somme ou différence  de nombre relatifs en écriture fractionnaire .

Vous avez vu en 5^ème que :

« a » et « b »et « m » désignant des décimaux positifs , « m  0 »     :

(remarquez le mot : « positif », cela signifie que cela n’est pas vraie si les nombres sont relatifs négatifs )

Activité 1 :

Calculez  ( n’oubliez pas de simplifier )

Vous avez aussi vu en 5^ème que : (remarquez le mot : « positif », cela signifie que cela n’est pas vraie si les nombres sont relatifs négatifs )

« a » et « b »et « m » désignant des décimaux positifs , « m  0 »     et  «  a

Activité n° …

Calculez ( n’oubliez pas de simplifier )

Ø Dans le cas de nombres relatifs en écriture fractionnaires

Ø  Info ++

Les additions et les soustractions se font comme avec les décimaux relatifs.

Activité n°….

Exemple :   

Fiche 6 : Réduction au même dénominateur.

Info : réduire au même dénominateur.

Situation problème :

On compte rembourser une somme d’argent en 3 fois.

La première fois, on en rembourse  le   «   » , la deuxième fois le «   »  . Quelle fraction de la somme reste-il à rembourser la troisième fois ?

Résolution :

1°) Calcul de la fraction  de la somme remboursée globalement  les deux premières fois.    .

Pour pouvoir additionner    , il faudrait que les dénominateurs soient égaux. ( on dit « réduites  au même dénominateur » )

Le dénominateur commun est un multiple de « 4 » et de « 6 » :          et  

On le choisit le plus petit possible. On prend alors :  «    »

 ( on dit que « 12 » est le Plus Petit Dénominateur Commun. ( PPDC) ) aux deux nombres « 4 » et « 6 »).

Nous savons que la somme à rembourser est représentée par la fraction

Donc la  somme qu’il reste à rembourser  correspond à la fraction   c'est-à-dire :   

Conclusion la troisième fois on rembourse les .

Activité n°1 :  Calculez comme précédemment   A  =  

Recherche du dénominateur commun :     ;

Le dénominateur commun le plus petit possible est : 

Ø Faites de même pour : 

   ;     ;   Le dénominateur commun le plus petit possible est : 

Ø Faites de même  pour 

Exemple : où il faut faire attention !!!!

  , n’oubliez pas de simplifier avant de réduire au même dénominateur

       et   ;   le dénominateur commun obtenu à partir des écritures simplifiées est :  « …. »

Ø Faites de même pour :

Ø  

Cas où l’un des termes est un entier.

Info + sur ……

Calculons :   , le dénominateur commun est « 6 »

  = 

Calculez de même :

Activité :  Avec des nombres relatifs fractionnaires.

 Calculez ( simplifiez si possible )

Info ++ sur les rationnels

Fiche 7 : Activités  Exercices et situations problèmes.

Exercices :

Activités 1 :

En procédant comme dans la fiche 6 , Calculez les sommes suivantes : ( avec des fractions pace que les termes sont des nombres entiers)

Activités n°2 : Complétez la table d’addition et la table de soustraction ( donnez l’écriture simplifiée)

Première entrée

Fiche 8 :   Situations problèmes.

Les situations problèmes proposées sont d’ordre de difficultés croissantes. ( les premières vous permettrons de résoudre les PB suivants)

Activités n°1 :

Quelle est la longueur ( L)  d’ne pelote de ficelle ( en m ) de la pelote  sachant que   de celle –ci mesure «  15 m » ?

On peut écrire  ( en m) que    ; D’où l’on en déduit ( voir la fiche 5  )  que  L =    = 35 m

La longueur de la pelote est de 35 m.

Activité n° 2 : Un réservoir est plein . On retire successivement    puis   puis  de son contenu.

Il reste alors 427 L . Quelle est la contenance de ce réservoir ?

Activité n° 3 : Un automobiliste constate à la jauge de son tableau de bord que son réservoir ne contient plus que  d’essence.

Il s’arrête à une station et prend 35 L d’essence , la jauge indique alors que le réservoir est plein au   .

Quelle est la contenance de son réservoir ?

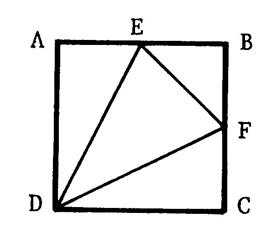
Activité n° 4 : « ABCD » est un carré de 1 m de côté.

« E » est le milieu de [ AB ]  et « F » le milieu de [BC ]  .

1°) Calculez les aires de « ABCD3 , « AED », « DCF » et « EBF »

2°) Quelle fraction de l’aire du carré représente l’aire de chacune des surfaces  « AED » , « DCF » et « EBF » ?

3°) Quelle fraction de l’aire du carré représente l’aire de « EDF » ?

Fin de la fiche§§§§§ (demandez le corrigé)

Fiche statistique :   classe 4^ème

Exploitation de données statistiques.

Info ++ sur les statistiques.

Dans un collège , la question suivante a été posée à 80 élèves :

«  Combien avez-vous de ères et sœurs ? »

On vous a retranscrit les réponses ci-dessous  (tableau de valeurs) :

1

3

0

1

0

2

1

1

1

0

0

4

0

2

2

1

3

1

0

2

6

1

1

2

2

2

0

1

1

3

0

0

3

1

0

1

2

4

4

1

1

2

2

0

1

0

0

3

0

4

2

2

1

1

1

1

4

0

1

3

3

2

0

0

4

2

1

1

3

2

6

0

3

5

0

0

1

2

1

1

Nombre de frères et sœurs.

0

1

2

3

4

5 et plus.

Effectifs.

16

Effectifs cumulés.

62

Fréquences ( en  %)

20

Fréquences cumulées ( en %)

77,5

1°) « EFFECTIFS » : Trouvez, en comptant dans la liste , le nombre d’élèves correspondant à chaque valeur et complétez le tableau.

Exemple : l’effectif correspondant à la valeur « 2 » est « 16 ». C'est-à-dire : « il y a  « 16 » élèves qui ont  « 2 » frères et sœurs.

L’ effectif total est la somme des effectifs des différentes valeurs . Ici , c’est ……………

2°) «  EFFECTIF CUMULE »

               L’effectif cumulé correspondant  à la valeur « 2 » est  le nombre d’élèves dont le nombre de frères et sœurs  est inférieur ou égal à « 2 ».

C'est-à-dire :  

·       Effectif valeur « 0 » + Effectif valeur « 1 » + Effectif valeur « 2 » =   20 + 26 + 16 =  62

Ou alors :

·       Effectif cumulé de la valeur « 1 » + Effectif de la valeur « 2 ».

Remarque : L’effectif cumulé de la dernière valeur est égal à l’effectif ……..

3°) FREQUENCES :

·       La fréquence d’une valeur est égale au quotient de l’effectif de cette valeur par l’effectif total. ( à retenir)

Par exemple : la fréquence de la valeur « 2 »  est  égal au rapport de     soit  = 0,2   (c’est un nombre décimal)

Remarque 1 : La somme des fréquences de chaque valeur  est égale à « … ».

Remarque 2 : La fréquence est souvent exprimée en pourcentage. 

Ainsi dans l’exemple précédent, la fréquence  qui est  0,2  est représentée par la fraction      ; ce que l’on traduira  «  …. % ».

( lire : vingt pour cent.)

Activité : complétez le tableau en donnant les fréquences en % . (prendre 2 chiffres après la virgule) .

4°) FREQUENCES CUMULEES .

On peut calculer les fréquences cumulées de deux façons :

-        A partir des fréquences  ( en les additionnant )

-        Ou à partir des effectifs cumulés ( on calcule les quotients). 

Activité : complétez le tableau en donnant les fréquences cumulées en % . (conservez les 2 chiffres après la virgule) .

5°) LES REPRESENTATIONS GRAPHIQUES.

(info . plus sur les représentations graphiques)

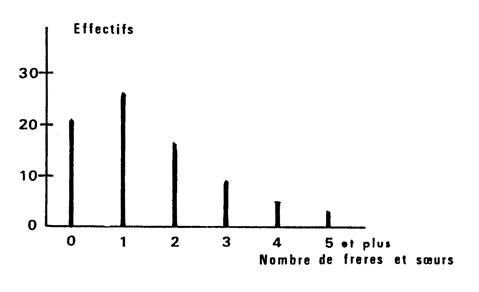
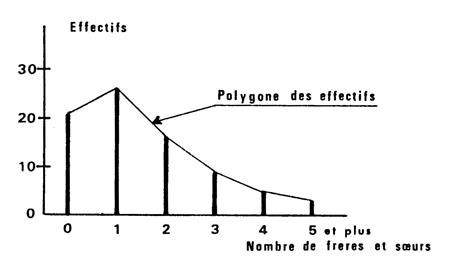
Ci-dessous, on vous donne le diagramme en bâtons des effectifs.

La ligne joignant les extrémités des bâtons s’appelle le « polygone des effectifs ».

Diagramme  en bâtons

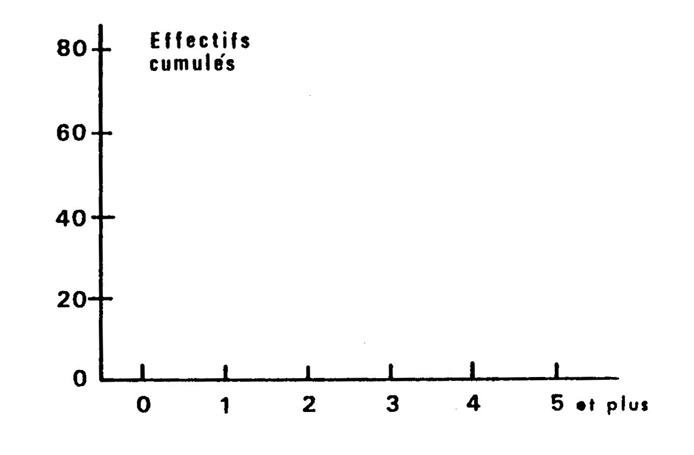
Activité : On vous demande de  dessiner de même le diagramme en bâtons  et le polygone des effectifs cumulés.