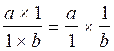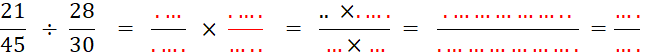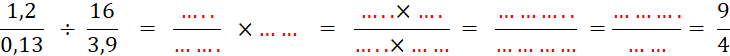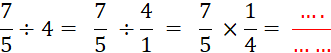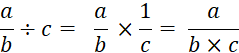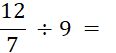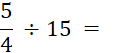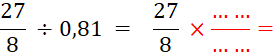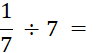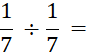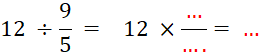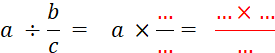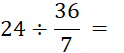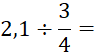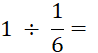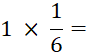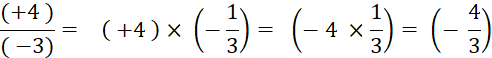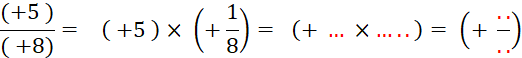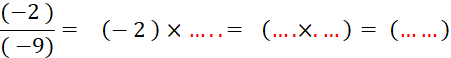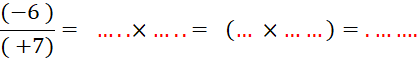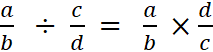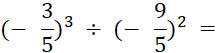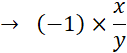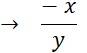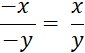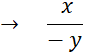Division de nombres relatifs au collège 4ème

	Rappels essentiels
	Fiche 1 : Inverse d’un nombre.
	Fiche 2 : Quotient de nombres positifs en écriture fractionnaire.
	Fiche 3 : Calcul du quotient.
	Fiche 4 : Exercices et situations problèmes.
	Fiche 5 : Quotient de nombres relatifs. ( et en lien avec les calculs algébriques)

TEST

COURS

Devoir Contrôle

Devoir évaluation

Interdisciplinarité

1°) situations problèmes

Corrigé Contrôle

Corrigé évaluation

COURS

Rappels essentiels :

I ) « la valeur absolue » est la valeur arithmétique du nombre relatif.

II ) Se souvenir qu’ à chaque fois que l’on fait un calcul avec deux nombres relatifs on recherche un troisième nombre relatif dont on devra rechercher : « sa valeur absolue » et « son signe ». (dans des parenthèses)

III) DIVISION : Le quotient « a : b » est le résultat d’une division (de deux nombres)

IV ) On dit aussi que la division peut se transformer en multiplication.

Voir « la fraction : @ nomenclature »

Démonstration :

nous savons que a : b s’écrit et que « l’inverse de b » s’écrit

Nous pouvons écrire que est égal a la multiplication ; puisque est égal à inv.b on peut écrire que = a inv.b

Nous pouvons dire que : La division est égal au produit dividende par l’inverse du diviseur .

On ne traite que deux nombres à la fois

V) Pour comprendre ce qu’est un nombre relatif se souvenir qu ‘un nombre négatif représente de « l’argent dû » (une dette ; de l’argent en « moins » ) et qu’un nombre positif représente une « rentrée d’argent ». (de l’argent en « plus »).


INFO COURS : sur la division de deux nombres relatifs.

Fiche 1 : Inverse d’un nombre			Info @ plus sur « inverse d’un nombre »
Vous avez déjà vu dans une leçon précédente ( info@)) que par exemple : sont des « inverses » l’un de l’autre et on peut écrire : ce qui nous permet d’écrire que Activité 1 : Complétez de même et D’une manière générale , vous savez que :
		« » et « » étant des nombres ( ou des grandeurs) quelconques , « » et « » étant des décimaux positifs non nuls, dire que c’est dire que et sont dits « inverses » l’un de l’autre.
Activité 2 :
	a pour inverse : et on a « » a pour inverse et on a a pour inverse
· Ainsi « » et « » étant des décimaux positifs non nuls, à pour inverse et Tout nombre positif non nul a un inverse. Le produit d’un nombre positif non nul par son inverse est égal à « 1 ». On peut prouver que c’est le seul cas où le produit de deux nombres est égal à « 1 ».

Cas des nombres négatifs. Cherchons si , par exemple , possède un inverse. Pour cela , cherchons un nombre dont le produit par est égal à « 1 ». Vous constatez déjà que le nombre cherché doit avoir le signe « moins » et puisque « » a pour inverse « » , alors a pour inverse et ….. = 1 Il est possible de prouver que : est le seul nombre dont le produit par est égal à « 1 ». Il en est de même pour tout nombre négatif .
Activité n°3. Complétez équivaut à

A retenir : « » étant un nombre relatif non nul , « » possède un inverse unique. C’est le nombre dont le produit par « » est égal à « 1 » .

Activité n° 4. Situation problème : Un récipient plein d’eau pèse « 9,6 kg » . On en vide les « » , il pèse alors « 6 kg ». Combien pèse le récipient vide ?


Fiche 2 : Quotient de nombres positifs en écriture fractionnaire.

Rappel : « » et « » étant des décimaux positifs « » , le quotient de « a » par « b » existe toujours, il s’écrit « » ou « ». Il peut être « entier », « décimal » ou « non décimal ». C’est le nombre par lequel il faut multiplier « » pour obtenir « ».

Activités exemples :
signifie que	signifie que		signifie que

· De même ,avec les nombres en écriture fractionnaire, on écrira : ( par exemple ) signifie que

Définition : « » , « » , « », « » étant des décimaux positifs , « », « », « »,, on appelle « quotient » de par noté le nombre ( si il existe ) tel que
		= signifie


Fiche 3 Calcul du quotient.
« E » et « F » étant deux nombres quelconques. Par définition , « » signifie Or , vous savez que signifie que c'est-à-dire que et on peut donc écrire que · Ce que l’on vient de faire avec le nombre on peut le faire avec tout autre nombre no nul. On dira alors : « diviser par un nombre non nul , revient à multiplier ce nombre par son ……….. Puisque l’inverse d’un nombre non nul existe toujours , le calcul du quotient par un nombre non nul est toujours possible. On dira alors :
A retenir : « » , « » , « », « » étant des décimaux positifs , « », « », « » ( dit aussi non nul ) , le quotient de par existe toujours . Il est égal au produit de par l’inverse de :

Activités n° ….
Calculez :




Division par « 5 » .
« a » étant un nombre quelconque , donc
Règle :	Pour diviser un nombre par « 5 » , on peut :
	Ou	- Multiplier ce nombre par « 2 » puis diviser le résultat par « 10 »
		- Diviser ce nombre par « 10 » puis multiplier le résultat par « 2 »

Activité n° ..

Fiche 4 : Exercices et situations problèmes.

Situation problème n°1 :

Une vis avance de de millimètres par tour.

1°) Combien doit-elle faire de tours pour avancer de 10 mm ? …………

2°) Combien doit-elle faire de tour pour avancer de de mm ? ………………

v Quotient d’un nombre positif en écriture fractionnaire par un décimal positif.

Info @ ++ sur le calcul des quotients de….+

« » , « » , « » étant des décimaux positifs , « b » non nul et « c » non nul ,

Activités n°…

Calculez :

Situation problème n°2 :

Le tiers d’une somme d’argent est réparti équitablement entre quatre personnes.

Quelle fraction de la somme totale représente la part de chaque personne ?

v Quotient d’un nombre positif par un nombre positif en écriture fractionnaire.

« » , « » , « » étant des décimaux positifs , « b » non nul et « c » non nul ,

Activités n°…

Calculez :

Situation problème n°3 :

Avec un tonneau de « 70 » litres de vin , on veut remplir des carafes .

1°) Combien de carafes de « 2 » litres remplira-t-on avec le vin contenu dans ce tonneau ?

2°) Combien de carafes de « » litre remplira-t-on avec le vin contenu dans ce tonneau ?

3°) Combien de carafes de « » litres remplira-t-on avec le vin contenu dans ce tonneau ?

· Division par « 0,1 » ; « 0,01 » ; « 0,001 » ; etc…….

Info @ déjà vu

« » étant un nombre quelconque , « » ; de même « »

Ainsi « »

Règle :

Diviser un nombre par « 0,1 » ; « 0,01 » ou « 0,001 » ; etc……revient à multiplier ce nombre respectivement par « 10 » ; « 100 » ; « 1 000 » ;…etc…

Activité n° ..

On vous demande de calculer « mentalement ».


Fiche 5 : Quotient de nombres relatifs. ( et calculs algébriques)

« » et « » étant deux nombres relatifs ( On appelle « quotient » de « x » par « y » , noté ou le nombre « » tel que « »
	signifie que « »	« » signifie « »

Activités n° 1 :
	signifie que
	. ….. signifie que . ……
	= . ……………………. signifie que
· Vous pouvez contrôler sur ces exemples que la règle de calcul est la même que dans la « fiche 2 ».

A retenir : Pour calculer le quotient de deux nombres relatifs ( pris dans un ordre déterminé ), on multiplie le premier par …………… du second.



Remarque : La règle des signes de la division est la même que celle de la multiplication.
· Puisque , alors l’inverse de qui est égal à Aussi : « » et « » étant des décimaux relatifs non nuls , vous pouvez dire que l’inverse de est
A retenir : « » , « » , « » , « » étant des décimaux relatifs ( « b » , « c » , « d » non nuls ) :

Activités n° :




· Inverse d’un nombre relatif.
On a vu que tout nombre relatif non nul possède un inverse unique. En désignant l’inverse de « » par « » , on peut écrire « » Or « » signifie « » c'est-à-dire « »
A retenir : « » étant un nombre relatif non nul , l’inverse de « » s’écrit « » « » et « » étant des nombres relatifs ( ) , «

· Différentes significations de « »
« » et « » étant des nombres relatifs ( ) , · Transformons l’écriture de « » : « » · Transformons l’écriture de « » : « »
« » et « » étant des nombres relatifs ( ) , Opp. , , , , sont des nombres égaux que l’on écrit			Opp.


Cas particulier :


Fini le 26 / 10 / 2014