1°) Mesure du volume d’un parallélépipède rectangle.

2°) Unités de volume – Système métrique.

3°) Changement d’unité : conversion.

4°) Unités de capacité.

5°) Calcul du volume du parallélépipède rectangle et du cube.

6°) Situations problèmes.

FICHE de travail :

·       Mesure du volume d’un parallélépipède rectangle.

Info ++sur les notion de l’unité de volume+

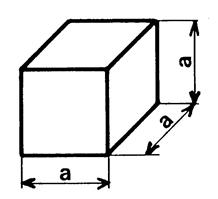
On décide de prendre « le cube » comme « cube unité »

Nous appellerons « U » cette unité.

  ou  vu autrement  

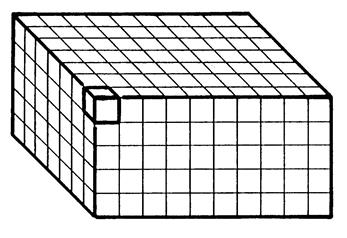
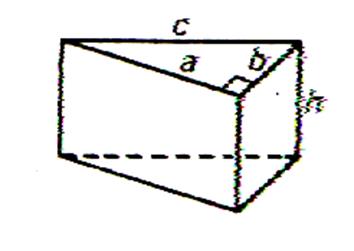
Considérons le parallélépipède rectangle, ci contre , vu en perspective (info +++).

                On se propose de déterminer par le dénombrement combien  de « cube unité » composent  ce parallélépipède.

Procédure :

Nombre de cubes sur la longueur de face : ……10…..

Nombre de cubes sur la profondeur : ………7……..

Nombre de cubes constituant une couche :  10 … …7….= …70 ..

Nombre  de couches :  …5……

Nombre total de cubes :  70 …  .5…..= …350……

En définitive, le nombre total de cube est obtenu en effectuant le produit : ……10 ….……7…..……5……..= ……350 …...

On dit alors que le nombre « 350 » est la mesure , avec l’unité « U » , du volume du parallélépipède rectangle.

En appelant »V » le volume du parallélépipède , on peut écrire :  « V = 350 U »

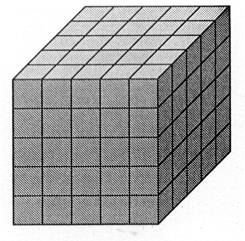
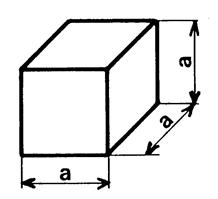
De la même façon : avec l’unité « U ».

La mesure du volume du cube ci-contre est obtenue en effectuant le produit : ……5 ….……5…..……5……..= ……125 …...

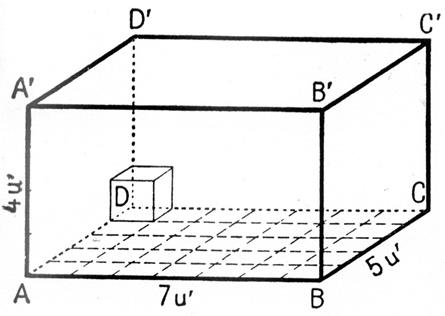
Figure 1 : De la même façon : avec l’unité « u’ »

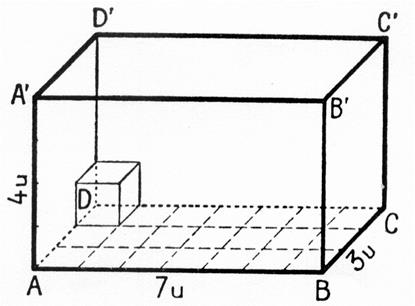
Figure 2 : De la même façon : avec l’unité « u »

La mesure du volume du parallélépipède est :

……7 u’….……5 u’…..……4 u’…..= ……140 u’ …...

La mesure du volume du parallélépipède est :

……7 u….……3 u…..……4 u……..= ……84 u …...

2°) Unités de volume – Système métrique.

Info 1 plus : système métrique.

Info 2 plus : les unités de volume et capacité.

Nous avons vu les unités de longueur : dont l’unité principale est le « mètre »……

Et les unités de volumes sont définies à partir des unités de longueurs.

Le « mètre cube » est le volume  d’un cube dont la longueur de l’arête est « 1 » mètre.

Il en est de même pour les autres unités .

Par exemple :

-         Le « décimètre cube » est le volume d’un cube dont la longueur de l’arête est « 1 » décimètre.

-         Le « centimètre cube » est le volume d’un cube dont la longueur de l’arête est « 1 » centimètre.

-         Le « millimètre cube » est le volume d’un cube dont la longueur de l’arête est « 1 » millimètre………

Symbole d’écriture :

·       Le symbole du mètre cube est « m ³ »

·       Celui du décimètre cube est  …« dm ³ »

·       Celui du centimètre cube est  …« cm ³ »

·       Celui du millimètre cube est  …« mm ³ »

·       ………………

Correspondance : 1 mètre cube vaut ……………………décimètres cubes..

Considérons un cube de « 1 m » de côté. Son volume est donc « 1 m³ »

Cherchons combien il contient de cubes de « 1 dm » d’arête  soit le cube dont le volume est de « 1 dm³ ».

En faisant le même raisonnement qu’au chapitre « 1° » et sachant que   « 1 m = 10 dm »

Vous pouvez dire que le nombre de cubes cherché est :  ……10….……10…..……10…..= ……1 000  …...

On peut alors écrire :

« 1 m³ »  =   « 1 000 dm³ »

Complétez le tableau ci-dessous :

Unité

Symbole

Correspondance avec le mètre cube.

mètre cube

« m ³ »

décimètre cube

« dm ³ »

« m ³ » =……1 000 ………«dm ³ »

« dm ³ » =………0,001……«m ³ »

centimètre cube

« cm ³ »

« m ³ » = ……1 000 000…..«cm ³ »

« cm ³ » = ……0,000 001…..«m ³ »

millimètre cube

« mm ³ »

« m ³ » =…1 000 000 000…«mm ³ »

« mm ³ » =…0,000 000 001……«m ³ »

Voir le tableau de conversions….

Vous constatez que les unités successives  vont de « 1000 »  en « 1 000 ».

Donc , dans des changements d’unités, on découpera le nombre  en tranches de «  ..3.. » chiffres.

Complétez :

1  dm ³ = ………1 000…………….cm ³

1  cm ³ = …………1 000…………….mm ³

1  dm ³ = …1 000 000……….mm ³

1  cm ³ = ………0,001………….dm ³

1  mm ³ = ……0, 001……….cm ³

1  mm ³ = …0,000 001………….dm ³

3°) Changement d’unité : conversion.

« m ³ »

« dm ³ »

« cm ³ »

« mm ³ »

0

0

0

0

7

3

8

2

4

9

0

1

Dans le tableau ci-dessus, on a placé un nombre.

On peut lire indifféremment :

73,824901  dm³

Ou      0,073824901 m³

Ou   73 824,901 cm³

Ou   73824901 mm³

Activité 1 : En plaçant dans le tableau les nombres ci-dessous, faites les conversions.

5 m³  487 dm³ 12 cm³

= ……………………………. cm³

= ……………………………. dm³

= ……………………………. mm³

78 cm³  134 mm³

= ……………………………. cm³

= ……………………………. dm³

= ……………………………. m³

963 m³   4 dm³

= ……………………………. m³

= ……………………………. dm³

= ……………………………. cm³

Corrigé

« m ³ »

« dm ³ »

« cm ³ »

« mm ³ »

0

0

0

0

7

3

8

2

4

9

0

1

5 m³  487 dm³ 12 cm³

5

0

0

0

0

0

0

+

0

4

8

7

0

0

0

+

0

0

0

0

0

1

2

=

5

4

8

7

0

1

2

78 cm³  134 mm³

7

8

+

1

3

4

=

0

0

0

0

0

0

7

8

1

3

4

963 m³   4 dm³

9

6

3

+

4

=

9

6

3

0

0

4

0

0

0

0

0

0

Activité 2 : Complétez le tableau ci-dessous  dans lequel chaque colonne correspond à un même volume mais exprimé avec des unités différentes.

m³

0,53

0,000078529

0,000 000 64

0,00975268

dm³

530

0,078529

0,000 64

9,75268

cm³

530 000

78 , 529

0,64

9752,68

mm³

53 000 000

78 529

640

9752680

« m ³ »

« dm ³ »

« cm ³ »

« mm ³ »

0

0

0

5

3

0

0

0

0

0

0

0

0

0

0

0

0

0

0

0

0

6

4

0

0

0

0

0

0

9

7

5

2

6

8

0

0

0

0

0

0

0

0

7

8

5

2

9

4°) Unités de capacité.

Info ++ sur les mesures de capacité

Il arrive souvent que l’on doit mesurer « la quantité » de produit en poudre,  grain ou liquide,…….

Pour cela on prendra un récipient « contenant » pouvant mesurer ces produits.

Ces contenants ont des « capacités » déterminées.

Les unités choisies portent le nom d’ « unités de capacité » .

L’unité de capacité principale porte le nom de « litre ».

Le litre est la capacité d’un récipient dont le volume intérieur est de «  1 dm³ ».

1 L = «  1 dm³ »

Unité

Symbole

Correspondance avec le litre

Multiples usuels

hectolitre

hL

1 hL =  100 L

1 L  = 0,01 hL

décalitre

daL

1 daL =  10 L

1 L  = 0,1   daL

Litre

L

Sous multiples

décilitre

dL

1 dL = 0,1 L

1 L = 10 dL

centilitre

cL

1 cL =  0, 01 L

1 L = 100 cL

millilitre

mL

1 mL = 0, 001 L

1 L = 1 000 mL

Cherchez la correspondance avec   1 cm³ =  1 ………………….

Activité 3 :

Complétez le tableau ci-dessous.

37   hL

= ……3700…..L

= ……0,37……. m³

= ……3700….. dm³

= ………370…..daL

17,5 cL

= ……1,75……..L

= ……0,017…..hL

= ………1750.. cm³

= …1750000. mm³

0,000057 m³

= ……0,057…..L

= ………57…. cm³

= ………57….m.L

= ……0,00057..hL

Activité 4 :

Rangez dans l’ordre croissant…..

2350 cl

0,05635 m³

18,25 l

0,0809 hl

16 300 cm³

85 cl

Convertissons !!

En …  litre

5°) Calcul du volume du parallélépipède rectangle et du cube.

a)      Volume du parallélépipède rectangle.

Info +++

Nous reprenons le parallélépipède rectangle vu ci-dessus.et le petit cube  appelé « cube unité ».

Si la longueur du côté du petit cube est de « 1 cm » alors son volume sera de «  1 cm³ » ; «  lire : un centimètre cube ».

Les dimensions du parallélépipède rectangle sont « 10 cm » , « 7cm », « 5cm ».

D’après ce que l’on a vu sur le chapitre 1 , pour calculer son volume « V » en « cm³ » , on effectue le produit 

……10 ….……7…..……5…..= ……350  cm³  …...

Et d’une manière générale :

( à retenir)

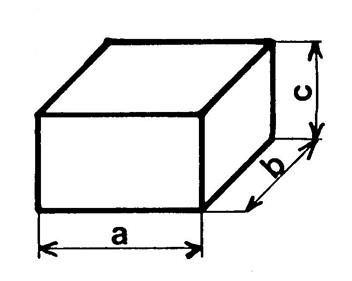
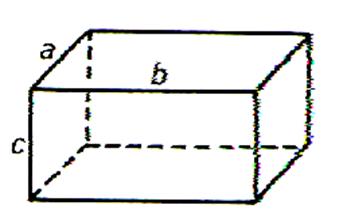
Une unité de longueur étant choisie, « a », »b », »c » étant les dimensions d’un parallélépipède rectangle son volume « V » (avec l’unité correspondante) est :

V =…a ….……b…..……c…..

A savoir 1 :

Le raisonnement vu au chapitre 1 a été fait avec des nombres entiers.

Dans le cas des nombres à virgule, il suffit d’imaginer un changement d’unité donnant des nombres entiers et on se retrouve dans la même situation.

Exemples  : « 5,3 ( nombre décimal)  cm devient 53 mm  (nombre entier) » ; « 1,25 m  se convertit en 125 cm »

Activité 3 :

Calculez le volume du parallélépipède rectangle dont les dimensions sont : 1,25 m , « 3,5 dm » , « 250 mm ».

Exprimez le résultat en centimètres cubes.

Conseils : il faut convertir tout en centimètres.   : « 1,25 m =125 cm » , « 3,5 dm = 35 cm » , « 250 mm = 25 cm».

V = 125 fois 35 fois 25 = 118 125 cm³    ou  118,125 dm ³

A savoir 2 :

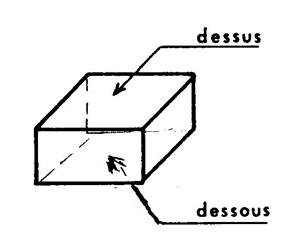
« Aire latérale »

On parle parfois d’aire latérale du parallélépipède rectangle.

L’aire latérale est l’aires des 4 faces autres que le dessus et le dessous.

Remarque 1 : si votre chambre à la forme d’un parallélépipède, l’aire latérale est l’ aire des quatre murs , on exclut donc le sol et le plafond de la chambre. 

Remarque 2 : la somme des aires  des 6  faces d’un parallélépipède est appelée  « aire totale » .( « on » dit parfois « surface totale »)

Activité 4 :

« a »

« b »

« c »

« aire latérale  »

« Aire totale »

« volume »

120 cm

30 cm

5 cm

2 (120 + 30)  fois 5=

………1 500……..cm²

…2 ( 120 + 30 ) + 1500 = ……1800…..cm²

= …120 fois 30 fois  5=.

18 000 c m³

5 m

30 dm = 3 m

120 cm= 1,2 m

………………………..m²

………………………..m²

= ……………. m³

…………..dm

7  m= 70 dm

25 cm= 2,5 dm

…74  fois 2,5 =…185.dm²

185 +560 = 745..dm²

= …700…. m³

280 / 70= 4

Surface de base :  700/ 2,5 = 280 dm²

9 dm = 90 cm

20 mm= 2  cm

276 / 184= 1,5……cm

………276…….cm²

………………………..cm²

= ……………. dm³

125 mm

50 / 12,5 = 4 cm

= 40 .mm

30 000 : (125fois40)= 6 .mm

……19,8……..cm²

…1, 198…..dm²=  119,8 cm²

= ……30…. cm³

b)     Volume du cube.

Info +sur le volume du cube ++

Un cube est un parallélépipède rectangle particulier dans lequel :

« a =b= c ».

Le volume du cube est alors :

V = a  a a

Par convention :

Info plus sur les puissances « cube »

« a » étant un nombre quelconque , « a  a a »   ,  s’écrit  «  a ³ »  . ( on lit :   « a » au cube )

Ainsi : « 2  2 2 »   ,  s’écrit  «  2 ³ »  . ( on lit :   « 2 » au cube ) ; «  2 ³ =    8 » 

Et  « 5  5 5 »   ,  s’écrit  «  5 ³ »  . ( on lit :   « 2 » au cube ) ; «  5 ³ =    125 » 

On dit que « 8 » est le cube de « 2 »  et que « 125 »  est le cube de « 5 » .

A retenir

Une unité de longueur étant choisie, étant donné un cube dont la mesure de la longueur  de l’arête est « a », son volume « V » (avec l’unité  correspondante ) est « V = a ³  » 

Activité 5 :

Complétez le tableau donnant les cubes des 11 premiers entiers naturels.

a

0

1

2

3

4

5

6

7

8

9

10

11

a ³

0 ³

1 ³

2 ³

3 ³

4 ³

5 ³

6 ³

7 ³

8 ³

9 ³

10 ³

a ³

0

1

8

27

64

125

216

343

512

729

1 000

1331

Activité 6 : (difficile : vous aider des résultats précédents )

Quelle est la longueur de l’arête d’un cube dont le volume est « 0,343 » dm³   :    réponse 0,7 dm  ( voir le cour sur la racine cubique d’un nombre)

Activité 7 : (difficile : vous aider des résultats précédents )

Quelle est la longueur de l’arête d’un cube dont le volume est « 0, 000064 » dm³   :    réponse : 0,04    ( voir le cour sur la racine cubique d’un nombre)

Activité 8 : (difficile : vous aider des résultats précédents )

Le volume d’un cube est de « 300   ». On appelle « a » la mesure en « cm » de son arête.

Donnez les valeurs approchées à 0,1 prés par défaut et par excès de « a ».

6°) Situations problèmes.

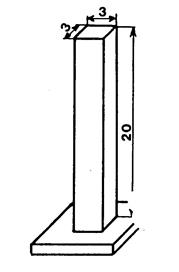
Pb 1 :

Le récipient en verre ci-contre  est un vase.

C’est un parallélépipède rectangle dont les dimensions intérieures sont « 3 cm » , « 3 cm », et « 20 cm » de hauteur.

1°) Il contient de l’eau. On immerge  un objet.

L’eau monte (sans déborder ) de 8 cm .

Calculez le volume de cet objet .*( 3 fois 3 fois 8 = 72 cm^{3 )}

2°) On enlève l’objet et on immerge un petit cube de « 25  mm »

( volume du cube : 25 fois 25 fois 25 =  15625mm³)

Calculez l’élévation du niveau de l’eau ( en mm)

15625 / 900 = 17,36 mm environ soit  17 mm d’élévation…

Pb 2:

L’intérieur d’un bassin est un parallélépipède rectangle dont les dimensions sont «  2,5 m » , « 4,4 m » et « 2,1 m » de hauteur.

Il est rempli d’eau aux    de sa hauteur.

Calculez la quantité d’eau ( en hL) qu’il contient  lorsqu’il atteint cette hauteur..

Volume en mètre cube  d’eau «  ( 2,5 m x 4,4 m x 2,1 m )  »  = 15,4

Volume en litre d’eau = 15 400 dm3 soit 15 400 litres.

Pb 3:

Un bloc de glace à une forme parallélépipédique. Un parallélépipède  qui a pour dimensions : «  25  cm » , « 40cm » et « 60 cm ».

1°) sachant qu’un dm³ de  glace pèse  0,918 kg , déterminez combien pèse ce bloc (masse  en grammes) :

2°) Sachant qu’un litre d’eau pèse « 1kg » , quelle est la qualité d’eau obtenue en faisant fondre ce bloc ? ( litre )

Volume du cube : 25 fois 40 fois 60 = 60 000 cm ³ ;   =  60 dm ³ ;   calcul de la masse : 60 fois 0,918 = 55,08  kg   = 55 080 g

Pb 4 :

Sur un toit rectangulaire (horizontal) de 21 m sur 12m, il est tombé une couche de neige de 15 cm . La neige donne en fondant les « 1/9 » de son volume en eau.

Calculez la quantité d’eau ( en litre) obtenue par la fonte de cette neige.

Volume de la neige : 21 fois 12 fois 0,15 = 37,8 m³ ; soit 37 800 dm³ ;   volume d’eau :  37 800 ( 1 / 9 ) = 4200 litres.