|
. |
Géométrie : DOSSIER :
PERIMETRE- AIRE- VOLUME / / Objectif cours 14c |
|||||||||||
|
Pré requis: |
||||||||||||
|
|
||||||||||||
|
Le tableau de
conversion |
||||||||||||
|
ENVIRONNEMENT du
dossier: |
||||||||||||
|
Objectif
suivant : 1°)le tableau de conversion des unités
de volumes et capacité |
|
|||||||||||
|
|
|
|
|
|||||||||
|
|
Le cube. |
|
||||||||||
|
|
Les unités de volume : (démonstration par comptage ). |
|
||||||||||
|
|
MESURER UN VOLUME. |
|
||||||||||
|
|
MESURE
pour le bois de chauffage : le Stère. |
|
||||||||||
|
|
MESURE de CAPACITE : le
Litre |
|
||||||||||
|
|
A
) Les mesurent pour les liquides |
|
||||||||||
|
|
B
) Les mesurent pour les matières sèches. |
|
||||||||||
|
|
LE PAVAGE dite aussi mesure par comparaison d’un volume . |
|
||||||||||
|
|
CALCUL du volume d’ un
prisme ( parallélépipède rectangle ) |
|
||||||||||
|
|
|
|
||||||||||
|
|
||||||||||||
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
||||||
|
|
||||||||||||
|
|
||||||||||||
|
LES UNITES DE VOLUMES et de Capacités ; SYSTEME METRIQUE : Le « mètre cube » (noté :
m3 ) . ses Multiples et
sous-multiples. |
||||||||||||
|
|
COURS
|
|
|
|
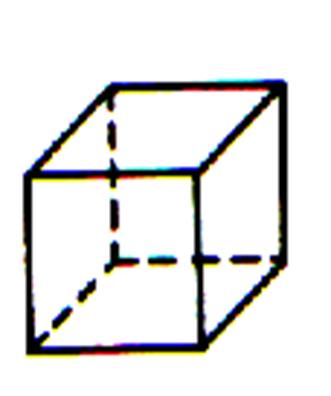
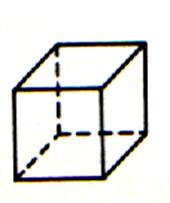
I ) le cube . |
|
|
|
On appelle « cube » un volume ayant la forme d’un dé à jouer , c’est à dire terminé par six faces carrées égales
entre elles ; tous les côtés du cube ont donc la même longueur. |
|
|
|
|
|
|
|
|
|
|
|
Unités de volume : |
|
|
|
On prend pour unités de volume les cubes construits sur les
différentes unités de longueur. L’unité fondamentale est le « mètre
cube » ou « cube » construit
sur le mètre qu’on désignait par le signe m.c. est
que l’on désigne maintenant par m3 .(m.c.= m3)
. Par
définition : Le "mètre cube"
est le volume occupé par un cube
de 1 m de côté. Ses multiples et sous multiples
sont : Multiples : Myriamètre cube (Mm.c. = M m3) ; kilomètre cube (Km.c.= K m3) ; hectomètre cube (Hm.c.= H m3) ;Décamètre
cube(Dm.c.=Da m3) ; Unité principale :
mètre cube (m.c.= m3) ; Sous multiples : Décimètre cube (dm.c.=d
m3) ; centimètre cube (cm.c.= c m3) ;
millimètre cube (mm.c.= m m3). Comme
dans les « aires » , nous avons des unités de
différents ordres , et il est facile de faire voir qu’une unité d’un
ordre quelconque vaut 1000 unités de l’ordre immédiatement inférieur . Montrons , par
exemple , que le mètre cube vaut 1000 décimètres cubes . |
|
|
|
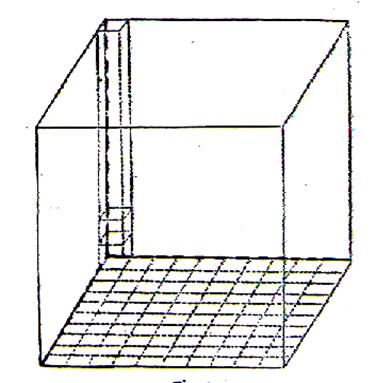
Prenons un carré de 1mètre de côté ; nous savons qu’il contient
100 décimètres carrés. Plaçons sur chacun d’eux un cube de un décimètre cube. |
|
|
|
|
|
|
|
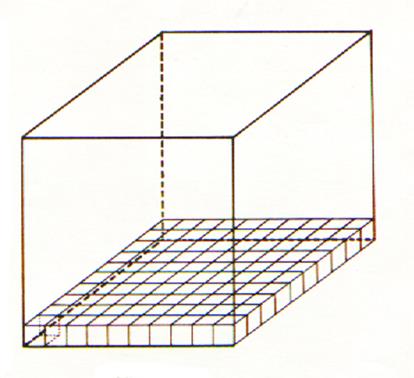
Nous formons ainsi une tranche ayant 1 mètre carré de base et 1
décimètre de hauteur et comprenant 100
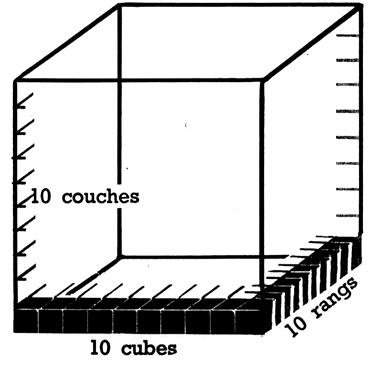
décimètres cubes. En superposant dix tranches ( couches)
semblables , nous obtenons un cube
ayant 1 mètre carré de base et 1 mètre de hauteur ; ce sera donc le
mètre cube . Or , il se compose de dix tranches (
couches) contenant chacune 100 décimètres cubes ; il contient donc 1000
décimètres cubes. Nous pouvons donc regarder les différentes unités de volume comme
formant deux séries , à partir de l’unité
fondamentale ou mètre cube : l’une ascendante et comprenant des unités
de mille en mille fois plus fortes , l’autre descendante et comprenant des unités
de mille en mille fois plus faible. |
|
|
|
|
|
|
|
Montrons
que le décimètre cube contient 1000 cubes de 1 cm d'arête |
|
|
|
A)
Soit un cube de 1 cm de côté:
|
|
|
|
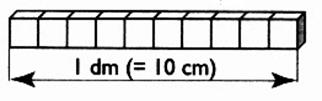
B)
10 cubes
de 1cm d'arête forment une barrette
de 1 dm de longueur.
|
|
|
|
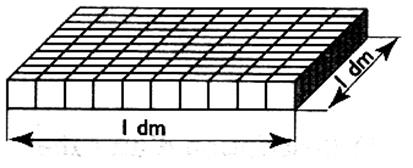
C ) 10
barrettes forment une plaque carré de
1 dm de côté . Cette plaque contient 100 cubes de 1 cm d'arête. |
|
|
|
|
|
|
|
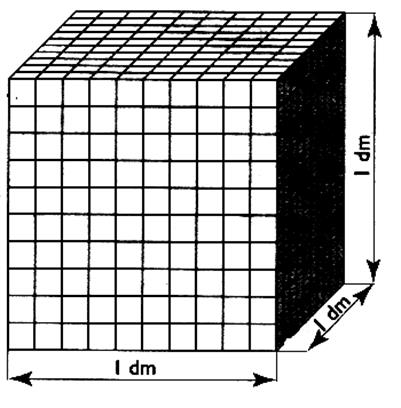
D ) 10
plaques de 1cm d'épaisseur , mesure un décimètre de hauteur. Ces 10 plaques contiennent chacune 100 cubes de 1 cm d'arête. Le cube de 1 dm d'arête contient donc 10 fois 100 cubes de 1cm cube . soit 1000 cm cube. Donc : 1 dm 3 = 1 000 cm3 |
|
|
|
|
|
|
|
MESURER UN
VOLUME. Mesurer un volume , c’est rechercher combien
il contient d’unités de chaque ordre. Puisqu’il peut y avoir jusqu’à 999
unités de chaque ordre , le volume sera représenté
par un nombre entier ou décimal , en ayant soit d’affecter 3chiffres à chaque
ordre d’unités. Supposons , par exemple , qu’on ait
trouvé qu’un volume contient 93
décamètres cubes 673 mètres cubes 36 décimètres cubes. Si nous prenons
le mètre cube pour unité principale , le volume sera
représenté par le nombre décimal 93673,036 m3 .. D’ailleurs nous
changerons facilement d’unité en multipliant ou divisant par 1000 ,
selon que nous prendrons une unité mille fois plus petite ou mille fois plus grande.
Supposons qu’un volume soit exprimé par le nombre 5075,3632 m3 , en
prenant le mètre cube pour unité principale. On pourra dire que le volume
contient : 5075 mètres cubes 3632 dix- millièmes. Si l’on veut énoncer les nombres des unités
des différents ordres que contient le volume , on
dira : 5 décamètres cubes 75 mètres cubes 363 décimètres cubes et 200
centimètres cubes. Si l’on prenait le centimètre cube comme unité principale ,le volume serait exprimé par le
nombre :5075363200 cm3 Cliquer ici :Tableau de conversion |
|
|
|
|
|
|
|
MESURE
pour le bois de chauffage : le Stère : |
|
|
|
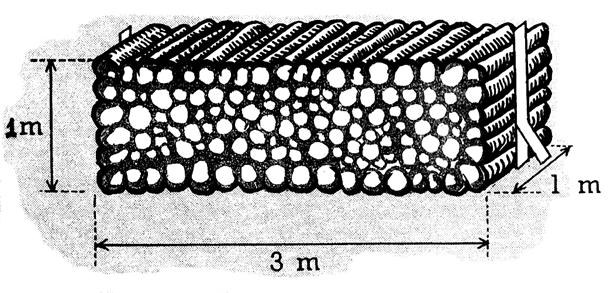
Lorsqu’on
veut mesurer le bois de chauffage , on prend pour
unité le mètre cube , auquel on donne alors le nom de « stère ». Le
stère n’a qu’un seul multiple , le
« décastère » , et un seul sous – multiple , le
« décistère » . On donne assez souvent au double stère le nom de
« voie métrique ». |
|
|
|
|
|
|
|
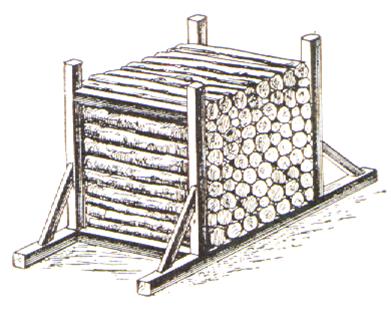
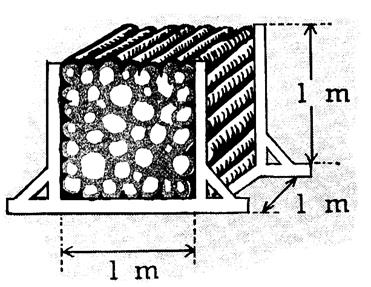
Le
stère qu’on emploie dans les chantiers pour mesurer le bois se compose d’une
traverse horizontale nommée « sole » , aux
deux extrémités de laquelle s’élèvent deux montants verticaux soutenus
extérieurement par deux pièces appelées « contre- fiches » . Les
deux montants ont un mètre de hauteur
et leur distance intérieure est aussi de 1 mètre . Il
résulte de cette disposition que si l’on couche horizontalement sur la sole des bûches de
1m et qu’on superpose plusieurs rangées de bûches jusqu’à ce que l’appareil
soit plein , on obtiendra un mètre cube ou un stère
de bois . Le
bois de chauffage se vend aussi au poids . La voie
métrique de chêne sec pèse environ 800 kilogrammes ,
de sorte que 1000 kilogramme de bois de cette essence représentent à peu prés 2,5 stères. |
|
|
|
|
|
|
|
|
|
|
|
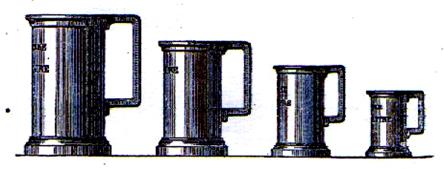
L’unité fondamentale des mesures de capacité pour les liquides et les
matières sèches est le décimètre cube qui prend le nom de litre
. On a adopté pour les mesures de capacité la forme cylindrique, qui se
prête mieux que la forme cubique aux usages auxquels ces mesurent sont
destinées. Les multiples du litre sont l’hectolitre ( Hl)
et le décalitre (Dl = Dal) , les sous multiples sont le décilitre ( dl) et le
centilitre (cl). On emploie aussi fréquemment les doubles et les moitiés des
mesures précédentes. A )
Les mesurent pour les liquides |
|
|
|
Les mesurent pour les liquides sont en étain ; le cylindre a une
hauteur double de son diamètre . Les dimensions du
litre sont « diamètre » : 86 millimètres ; hauteur :172 mm. |
|
|
|
|
|
|
|
Pour les matières sèches , telles que les
grains , les mesures sont en bois . La hauteur du cylindre est égale à son diamètre . La
rafle sert à niveler , à retirer le surplus. |
|
|
|
|
|
|
|
:voir
ici les informations sur le : Tableau de conversion des unités de capacité
|
|
|
|
|
|
|
|
LE PAVAGE dite aussi mesure par comparaison d’un volume : |
|
|
|
|
|
|
|
L’unité : est
appelé : Le « pavé » |
|
|
|
|
|
|
|
L’outil de mesure de volume est un cube d’arête de valeur 1 (1cm ; 1dm , 1m ;…..). le volume d’un cube de 1 cm d’arête s’écrira : 1
cm3 le volume d’un cube de 1 dm d’arête s’écrira : 1 dm3 ;……… |
|
|
|
|
|
|
|
La mesure se fait par empilage de cubes semblables. De façon verticale on dit « empilage » De façon horizontale on dira « pavage » :
|
|
|
|
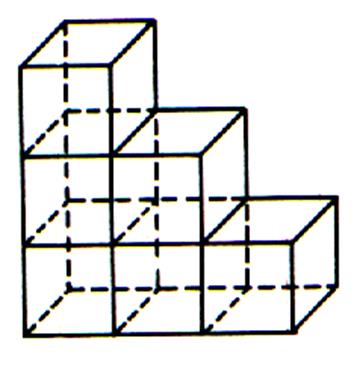
Pour trouver la valeur du volume ci contre on utilisera la technique
du « pavage » . On placera cote à cote des pavés de « 1 » d’arête. Une fois la base « remplit » !on passe à la couche suivante . |
|
|
|
|
|
|
|
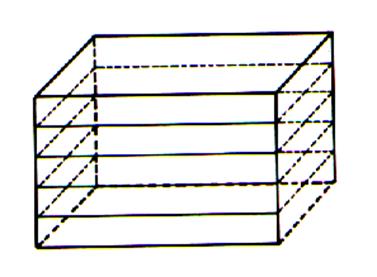
Ensuite on remplit l’ enveloppe du
volume par couches successives . |
|
|
|
|
|
|
|
Le remplissage terminé :Pour obtenir la
valeur du volume il suffit de compter le nombre de pavés qu’ il a fallu
utilisé pour remplir l’enveloppe . |
|
|
|
Et
du « vrac » : Le
volume occupé par les pavés n’est pas égal au volume de la matière
« grés » |
|
|
|
|
|
|
|
Et
du « rangé » : Le
volume occupé par les pavés est égal au volume de la matière (aggloméré de
sable et de ciment) |
|
|
|
|
|
|
|
|
|
|
|
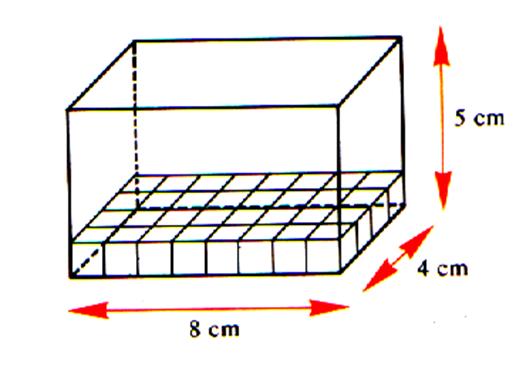
L’autre
méthode consiste à calculer le volume
à partir des dimensions que l’on connaît : Exemple : La première
couche contient : 8
fois 4 = 32 pavés de 1 cm de coté on
met (on superpose ) 5 couches pour remplir le
volume : soit 5 fois 32 cubes =160 cubes on
écrira : 160 fois 1cm3 soit
160 cm3 |
|
|
|
|
|
|
|
Le
tableau des unités de volumes utilise la numération en "base 1000" Il faut 1000 mm3 pour faire
1 cm3 , il faut 1000 cm3
pour faire 1 dm3
, il faut 1000 dm3
pour faire 1 m3 , il faut 1 000 m3 pour faire un dam3 ; il faut 1000
dam 3 pour faire un
hm3 et ainsi de suite …… Il faut
se souvenir que pour la surface on compte en "base 100"
et la
longueur on compte en "base 10" ( système décimal ) |
|
|
|
CONTROLE
I ) Quelles sont les unités principales de
mesure de volumes ?
EVALUATION
|
|
|
|
|
|