Pré requis:

Notion de surface

Le carré

ENVIRONNEMENT du dossier:

Index

AVANT : Le pavé

COURS

APRES : 1°) le carrelage et pavage .

Complément d’Info : Classe CM

TITRE : LES CARRELAGES ET LES DECOUPAGES

Travaux ; devoirs			Travaux et activités niveau VI et V Dossier 132 - 133	Corrigé
TEST	Contrôle	évaluation		Contrôle	évaluation

Interdisciplinarités : (matière concernée) : Des exemples de carrelage ( polygones réguliers)
F	H	Géo.	Vie quotidienne et vie familiale	Autres :	Sciences et technique	Physique Chimie Electricité	Statistique.

COURS

TRAVAUX PRATIQUES :

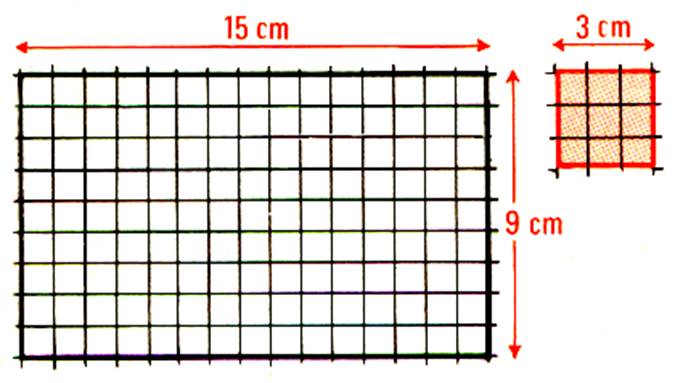
Découpons dans un cahier de dessin quadrillé : un rectangle de 15 cm de longueur et de 9 cm de largeur , puis un carré de 3 cm de côté. ( colorier le carré)il représente un carreau à placer .

Combien doit –on de disposer de carreaux pour couvrir le rectangle avec le carré ?

Imaginons que nous devons carreler le rectangle de 15 cm sur 9 cm avec des carreaux de 3cm sur 3cm de côté . Ce pourrait être un problème posé à un carreleur qui doit carreler une pièce .

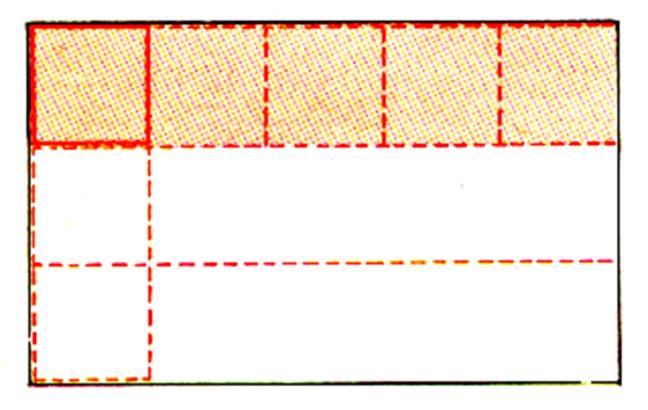
Voici ce que l’on obtient :

		Nous constatons que dans la longueur nous plaçons une rangée de 5 carreaux. Puisque nous pouvons placer 3 carreaux dans la largeur du rectangle , nous couvrons ce rectangle avec 3 rangées de 5 carreaux. Au total , nous devons disposer de 5 carreaux 3 = 15 carreaux
« Carrelage » et « mesure des surfaces » :
Mesurer une surface , c’est la découper en carreaux de même dimensions et compter le nombre de carrés . Mesurer en carrelant : c’est recouvrir une surface ;Comme on superpose deux surface , on dit aussi que c’est comparer cette surface à une autre surface ; l’unité étant le carreau « carré ».
L’unité fondamentale de mesure de la surface est un carreau « carré ». Le nombre de carreaux nécessaire à recouvrir la surface est la valeur de l’aire . Bien entendu il y a des grands , des petits ou des moyens carreaux . Les dimensions des carreaux sont dans le commerce différentes , cela est fonction du fabriquant .	SOS Cours Conversion d’unités

Pour rendre plus gai le décor , nous pourrions alterner les couleurs des carreaux ( ce que vous pouvez faire )

Activités supplémentaires :

Découper des rectangles de 20 cm de longueur et 12 cm de largeur , des carreaux de couleurs de 2 cm de côté , de 4 cm de côté .

Nous chercherons plusieurs motifs de carrelages.

Autre activité :

Découper des accès de 5 cm de côté dans une couverture de cahier qui mesure 22 cm de longueur et 17 cm de largeur .

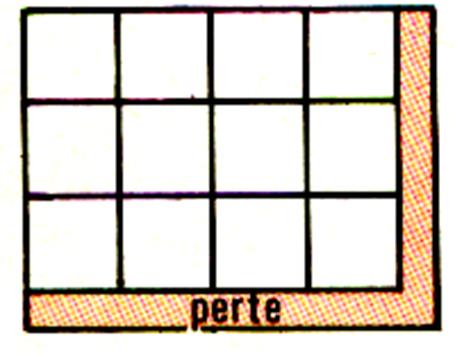
Résultat : Nous constatons que dans la longueur de la couverture tiennent 22 : 5 = 4 carrés Et que dans la largeur on peut découper 17 : 5 = 3 bandes de 4 carrés.

Nous pouvons donc découper 43 = 1é carrés seulement dans la couverture.

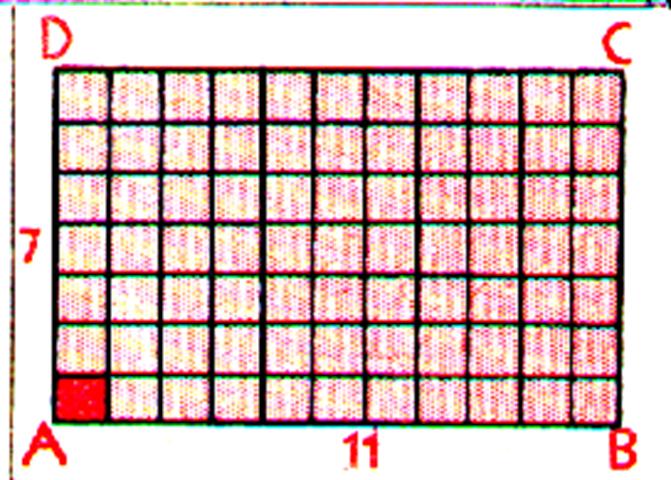
Les problèmes de carrelages et de découpages se résolvent toujours de la même manière.

Procédure : Il faut calculer le nombre de carreaux dans la longueur , puis dans la largeur . Enfin une multiplication donne le résultat .

Un bon croquis est indispensable.

TRAVAUX AUTO FORMATIFS.

CONTROLE:

Donner la procédure permettant de résoudre les problèmes de carrelages et de découpages :

EVALUATION:

Combien peut-on découper de carrés de 5 cm de côté dans une couverture de cahier qui mesure 22 cm de longueur et 17 cm de largeur ?.

Dans une feuille de bois de 45 cm de longueur et de 17 cm de largeur , combien un ouvrier pourra- t – il découper de carrés de 5 cm de côté ? de 10 cm de côté ? de 7 cm de côté ? de 8 cm de côté ?