Pré requis:

Représentation d’un parallélépipède  rectangle  dans l’espace
Les conversions  des unités de volume et capacité
Il n’existe pas de mot pour désigner la mesure d’un volume ! (  tel que le mot « aire » pour la mesure d’une surface). Nous conviendrons, dans ce qui suit, que l’expression     « volume d’un solide »  désigne en réalité la mesure de son volume de même que tout « segment» désigne la mesure de ce segment.

ENVIRONNEMENT du dossier:

Index : accueil warmaths.

Objectif précédent : 1°) Le cube .  notion ;……

Objectif suivant : Le cube 2°) Volume de prisme droit  volume du parallélépipède rectangle dit aussi : pavé droit.  Calcul d’aire et volume du cube

tableau    Leçons sur les volumes

DOSSIER :  L’ unité de volume « le  CUBE » ………  l’ unité  longueur à la puissance   ³    

et Détermination du volume  d’ un solide  par dénombrement ou par calculs.

	A )  Première notion .
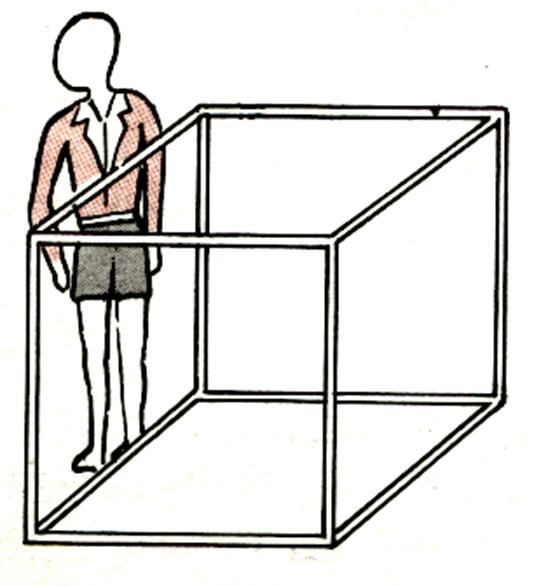
	B )  L’ UNITE (le cube de …1 m de coté »
	C ) Détermination de la valeur d’un volume.
	1) par  dénombrement ou « comptage » :
	2°) par comparaison
	3°) par calculs.
	·        Activités.
	·        Résumé

 

TEST	COURS	Devoir  Contrôle	Devoir évaluation 2°) Calcul « école »	Notions de volume .		Corrigé Contrôle	Corrigé évaluation
			Fiches n° travaux ……

 

 

COURS

A)  Première notion :

Une boite d’allumettes, une boite à chaussures ; un placard ; les emballages d’objets occupent une certaine place limitée par leur enveloppe. Cette place délimitée est appelée «  VOLUME »

Les objets occupent plus ou moins de place.

Pour donner une valeur numérique à ce volume occupé nous avons deux possibilités :

-         soit effectuer une mesure par comparaison.

-         soit effectuer une  addition et une multiplication » .

-         soit effectuer une  « double multiplication » .

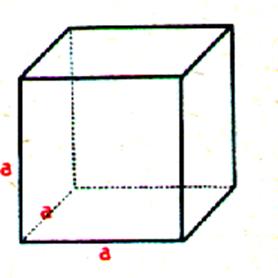
Il a été décidé que tout objet de forme prismatique ou quelconque est constitué d’un assemblage et empilage de  cubes . Les  dimensions des cubes « étalons » on été fixées par une assemblée de savants : Le cube est un prisme très particulier puisque la longueur de ses arêtes sont toutes de même longueur .

Ces cubes ont pour dimensions : 1 km d’arête ; 1 hm d’arête ; 1 dam d’arête ; 1 m d’arête ; 1 dm d’arête ; 1 cm d’arête ;1 mm d’arête  

Les principales unités usitées :

le mètre cube est un cube de 1m d’arête. soit : Longueur = 1m ;  largeur = 1m ;  hauteur = 1 m (il contient  1000 litres d’eau , ou 100 seaux de 10 litres)

 

 

B)  L’ UNITE .

 

= Le mètre cube   ( symbole  m³  )  :

Explication de l’écriture :   le « 3 »  placé en haut à droite du « m » est mis en « exposant » , on dit aussi « puissance de 3 » ou « au cube »

 

(info 1 ++ sur le mot « exposant »)   ; (info 2 sur : « puissance au cube »)

 

=Le mètre cube est le volume d'un cube dont le côté mesure 1 m .

Info niveau + :

On écrira  que le volume d’un cube de 1 mètre de côté est égal à    1 mètre multiplié par 1 mètre  multiplié par 1 mètre soit : =  1 m ´ 1m ´ 1m

(on peut écrire  que  1 m¹ ´ 1m¹ ´ 1m¹  est égal à =  1 m ¹⁺¹⁺¹  qui est égal à  1 m³  qui est égal après simplification   m ³ )

=Sous multiples :

Les sous multiples couramment utilisés  sont le décimètre cube ,  le  centimètre cube , le millimètre cube .

Le décimètre cube : ( symbole :  dm³ )

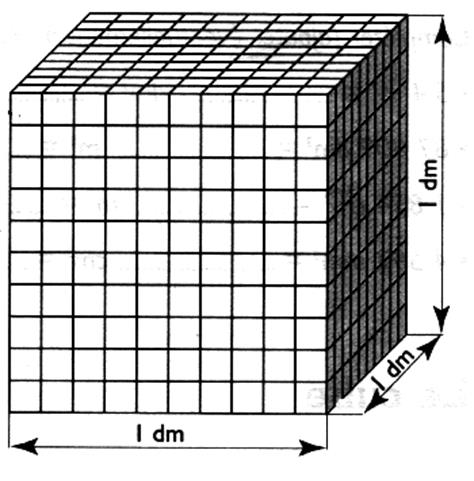
Le décimètre cube   est un cube de 10 cm d’arête .   Il contient en capacité 1 litre de liquide (eau ; huile ; …).   Ci contre : le     dm3

Le centimètre cube : ( symbole : cm ³ )

Le centimètre cube est un cube qui a un centimètre d’arête . Il contient un centième de litre ; soit 1  centilitre ( 1cl.)

 

 

C ) Mesure d’un volume : Pour donner une valeur numérique à ce volume occupé nous avons deux possibilités :

-         soit en effectuant un comptage .( addition et une multiplication ) 

-         soit effectuer une mesure par comparaison.(on plonge le corps dans un liquide contenu dans un récipient  « gradué)

-         soit effectuer une  « double multiplication » (ce type de calcul fera l’objet d’une étude particulière : à savoir @ : le volume d’un parallélépipède rectangle)  .

1) par  dénombrement ou « comptage » :

1a   Dans un cube de 1 mètre  d’arête , relation entre le décimètre cube et le centimètre cube :

A) Soit un cube de 1 cm de côté:
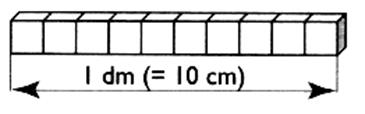
B) 10 cubes  de 1cm d'arête forment une barrette  de 1 dm de longueur.
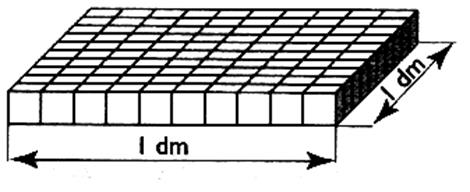
C ) 10 barrettes  forment une plaque carré de 1 dm de côté . Cette plaque contient 100 cubes de 1 cm d'arête.
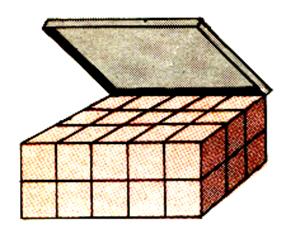
D ) 10 plaques de 1cm d'épaisseur , mesure un décimètre de hauteur.   Ces 10 plaques contiennent chacune 100 cubes de 1 cm d'arête. Le cube de 1 dm d'arête contient donc 10 fois 100 cubes de 1cm cube . soit 1000 cm cube.   Donc : 1 dm 3 = 1 000 cm3

 

Commentaire : pour obtenir le volume d’un objet on a trois possibilités : par  mesure ( dénombrement ;ou comparaison) ou par  dénombrement - calcul  ( addition et multiplication ) ; par calcul direct ( double multiplication).
1b  ) Mesure d’un volume par  dénombrement ou « comptage » :

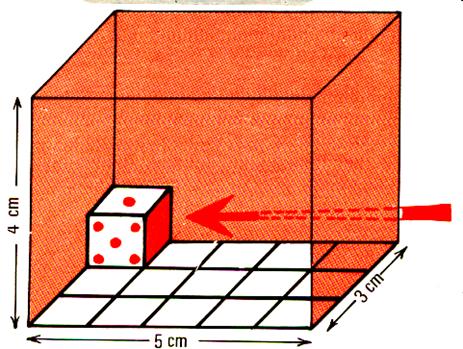
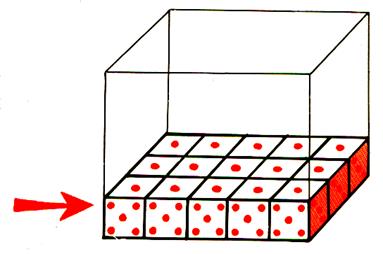
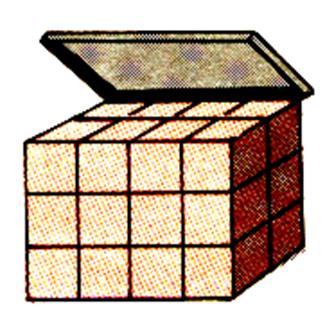
Exemple : Compter tous les cubes un par un , ( on vide  la boîte )

1°)  On veut  connaître le volume  contenu  dans l’enveloppe rouge ( grise) . C’est une boîte dont on a relevé les dimensions  avec une règle  graduée . Ces dimensions sont de 5 cm de long ; 3 cm de large , 4cm de haut .

Nous prenons des dés  ( cube) de 1cm de côté ; nous les rangeons pour en mettre le plus possible..

Un cube occupe la place d’un carré de 1 cm ; « au sol ». ! ! ! ! ! Par convention ( accord entre plusieurs personnes) on notera : cm3  pour un cube qui a  1 cm d’arête ;  dm3  pour un cube qui a  1 dm d’arête ,  mm3  pour un cube qui a 1 mm d’arête et ainsi de suite ; ……

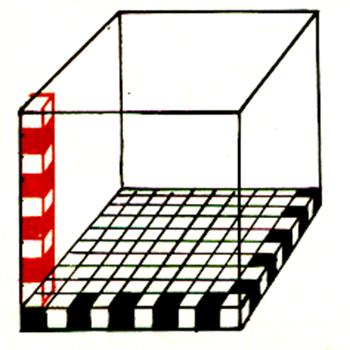
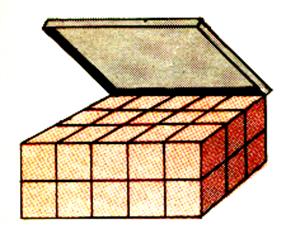
Premier remplissage : ( première couche)

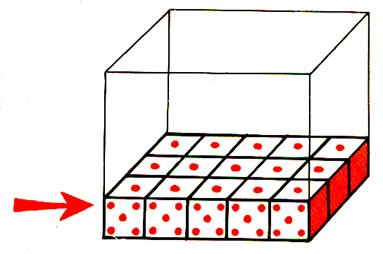
Nous avons  couvert toute la surface « au sol » On dit que l’on a  terminé le « 1er remplissage » avec 15 cubes de 1 cm de côté.
On écrira : Soit 15 « cube »de 1 cm. d’arête  Soit : 15 cm « cube » ; Pour finir on décide d’écrire :  15 cm3

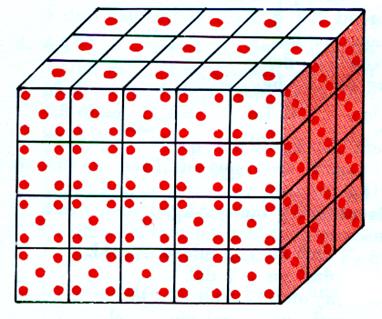
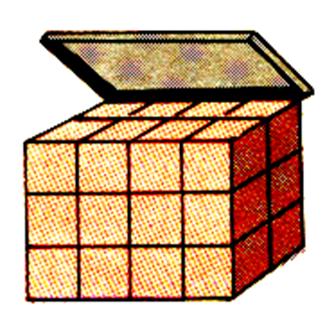
On remplit  par couches successives  jusqu ‘au haut ! ! !

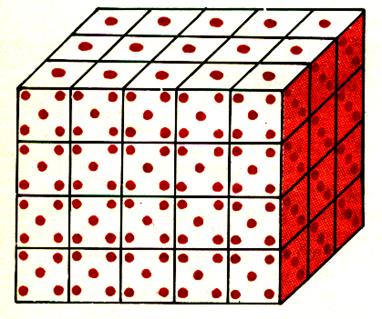
Successivement ;on remplit chaque couche ; Le remplissage est terminé ; les cubes de 1 cm de côté occupe tout le volume disponible par la boite . On compte 60 cubes de 1 cm de côté ..soit 60 cubes de 1 cm d’ arête . Ou : 415 cm3 = 60 cm3

 

 

1c  ) Deuxième possibilité : par addition et multiplication :

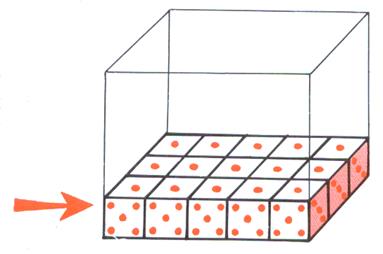
Nous avons  couvert toute la surface « au sol » On dénombre  15 cubes de 1 cm de côté.:
On écrira : Soit 15 « cube »de 1 cm. d’arête  Soit : 15 cm « cube » Pour finir on décide d’écrire :  15 cm3

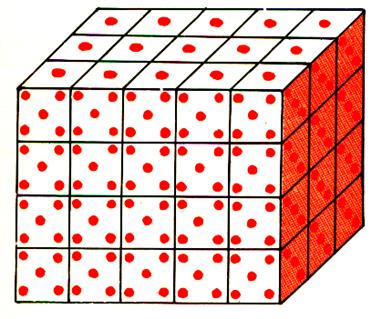
On remplit  par couches successives  jusqu ‘au haut ! ! !

Successivement ;on remplit chaque couche ; Le remplissage est terminé ; les cubes de 1 cm de côté occupe tout le volume disponible par la boite . Soit 4 couches de 15 cm3. Calcul :      415 cm3 = 60 cm3

2)Exemple de détermination de la valeur d’un volume de forme quelconque.

VOLUME :
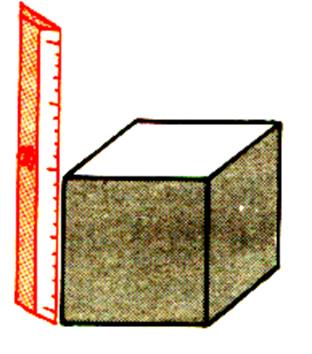
L’idée de volume peut être donnée par la portion de l’espace occupé par un corps . Ainsi par exemple : la règle occupe dans le tiroir une certaine place qui est son volume. Sur cette règle nous pouvons retrouver  les éléments définis précédemment. L ; l ; h .
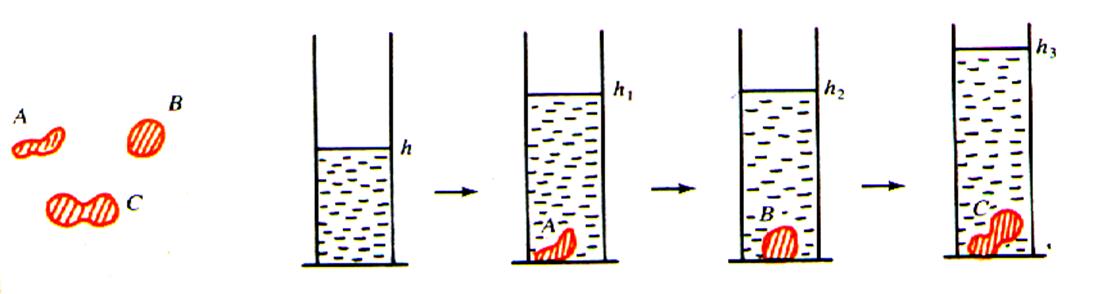
Expérimentation : Pour déterminer le volume des objectifs  A , B  et C ;de forme quelconque , on plonge cet  objet dans un liquide   ; l 'objet occupe son propre volume dans le liquide , il déplace ce liquide , le niveau monte dans l'éprouvette graduée.  le volume l'eau déplacé est égal au volume de l'objet
Reprendre cette expérience :  mettre dans le liquide des objets de volumes calculables ou non calculables : boites de conserve (forme parallélépipédique , cylindrique ;..) Comparer la hauteur avant plongé du solide dans le liquide  et lorsque le solide  est plongé dans le liquide. Au plus faire le calcul du volume du cylindre : ( V =  3,14 R 2 h )

 

3) Troisième possibilité : par double - multiplications.

 

Première multiplication :    le « 1er remplissage » s ’ opère avec  3 lignes de 5 cubes (Soit : 35 cm3 )ou  5 lignes de 3 cubes .( Soit : 5  3cm3 )
On écrira : Soit 15 « cube »de 1 cm. d’arête  Soit : 15 cm « cube » Pour finir on décide d’écrire :  15 cm3   :

 

Successivement ;on remplit la boîte  de  4 couches de 15 cubes de 1 cm de côté ; Soit 35 cm3   4 ; ou : 5  3cm3 4  ce qui donne :  15 cm3  4 = 60 cm3 soit 60 cubes de 1 cm d’ arête

 

4 ) ACTIVITES :

1°) Combien de cubes contient la boîte ?

Réponse :15 cubes

 

 

 

 

2° ) Combien de cubes contient la boîte ?

Réponse : 24 cubes

3°) Calculer le nombre de cubes  qu’il faut pour remplir le prisme ci - dessous . 

Il faut 10 10  = 100 cubes pour remplir la première couche ; et Pour remplir le volume total  il faut 10 couches de 100 cubes ; soit 1000 cubes . Si un cube de base mesure 1 cm ; l’enveloppe contient 1 000 cm3 Si un cube de base mesure 1 dm ; l’enveloppe contient 1 000 dm3 Si un cube de base mesure 1 m ; l’enveloppe contient 1 000 m3 Si un cube de base mesure 1 mm ; l’enveloppe contient 1 000 mm3

*  Recherche du volume occupé  par un solide n’ayant pas de dimensions précises.

En RESUME : (niv V)

Notion de volume. — Tout solide occupe une portion déterminée de l’espace appelée volume de ce solide.

L’égalité de deux volumes, les diverses opérations sur les volumes se défi­nissent comme cela a été fait pour les surfaces planes. Ainsi, le volume du polyèdre obtenu après juxtaposition de deux polyèdres donnés et suppression de la portion de face commune est, par définition, la somme des volumes de ces deux polyèdres. Cette juxtaposition peut se réaliser d’une infinité de façons et les divers polyèdres ainsi obtenus ne sont pas égaux, mais ont même volume, ils sont dits équivalents.

Deux polyèdres équivalents sont deux polyèdres qui ont même volume.

 

Unité de volume. — Les volumes sont donc des grandeurs mesurables.

 

On choisit pour unité de volume le volume du cube ayant pour arête l’unité de longueur.

 

A chaque unité de longueur correspond ainsi une unité de volume. L’unité principale de volume est le mètre cube (m³); on peut aussi utiliser le décimètre cube (dm³), le centimètre cube (cm³), etc.

Dans les énoncés relatifs aux mesures des volumes nous conviendrons que

1°)  Toutes les longueurs sont mesurées avec la même unité. (dans un calcul il faut « homogénéiser » les dimensions , Càd les exprimer dans la même unité de mesure)

2°)  Les surfaces et les volumes sont mesurés avec les unités de surface et de volume correspondant à l’unité de longueur adoptée.

Il n’existe pas de mot pour désigner la mesure d’un volume (  tel que le mot « aire » pour la mesure d’une surface). Nous conviendrons, dans ce qui suit, que l’expression « volume d’un solide désigne en réalité la mesure de son volume de même que tout « segment» désigne la mesure de ce segment.

 

On retiendra le  Théorème suivant

Le volume d’un parallélépipède rectangle est égal au produit de ses trois dimensions.

 

TRAVAUX AUTO _ FORMATIFS

 

CONTROLE :

Quelle est l’unité principale du volume ?

Donner la définition d’un cube ?

A quel calcul est égal le volume d’un parallélépipède ?

 

EVALUATION

 

1°) Dénombrer les cubes .

 

 

 

 

 

2° ) Combien de cubes contient la boîte ?