Pré requis:

Lecture : informations sur les prismes
Les perspectives ( historiques)
Les plans Frontaux et horizontaux
Les projections

ENVIRONNEMENT du dossier:

Index warmaths		Objectif précédent :informations sur la perspective linéaire .			Objectif suivant Les solides dans l’espace Ou : travaux sur les prismes droits en 5^ème		tableau 4 /liste des cours

DOSSIER « géométrie » : Les tracés en perspectives d’un parallélépipède rectangle
TEST	COURS		Devoir Contrôle	Devoir évaluation		Interdisciplinarité la perspective cavalière		Corrigé Contrôle	Corrigé évaluation

Parallélépipède rectangle vu en perspective cavalière

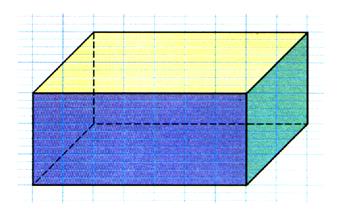
Conventions :

Les faces « bleue », « jaune » et « verte » sont celles que l’on voit.

La face « bleue » , à l’avant , est représentée par un rectangle.

Les faces « jaune » et « verte » ne sont pas représentées par des rectangles , mais leurs arêtes sont tracées parallèles.

spectiv2

COURS

Définition :

La perspective est une partie de la géométrie qui enseigne à représenter sur une surface (feuille ;….) des objets ayant des différences de formes, de dimensions et de couleurs dues à leur position.(image)

Représentation en perspective linéaire d’un prisme ( parallélépipède )

A ) en Perspective cavalière	B ) en Perspective axonométrique

Définitions relatives aux diverses positions d’un plan et d’une droite :

Définitions :

Exemples :

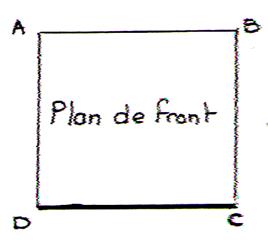
Plan et droite de front :

Un plan de front est un plan vertical placé bien en face de l’observateur

Une droite de front , ou frontale , est une droite quelconque d’un plan de front .

Une horizontale de front est une droite à la fois horizontale et de front .

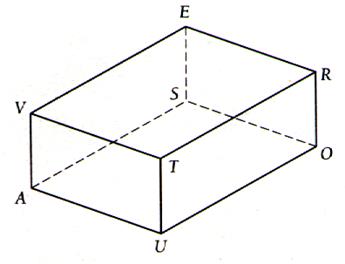
Pour matérialiser les définitions prenons une salle de classe rectangulaire :

Plaçons nous bien en face d’un de ces murs ; ce mur est le plan de front.

Les murs de droite et de gauche sont les murs de profils.

Les intersections du mur de front avec le plancher et le plafond , c’est à dire avec deux plans horizontaux sont des horizontales de front ;

Une droite quelconque du mur de front est une droite de front .

Les intersections des murs latéraux ou plans de profil avec le plancher et le plafond sont quatre droites de bout ; une droite quelconque d’un mur latéral est une droite de profil.

Plan de bout .

Un plan de bout est un plan perpendiculaire au plan de front.

Une droite de bout est une horizontale d’un plan de bout , c’est à dire une droite perpendiculaire au plan de front .

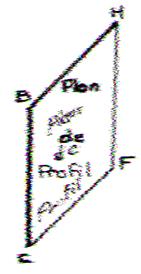
Plan de profil :

Un plan de profil est un plan à la fois vertical est de bout .

Une droite de profil est un droite quelconque d’un plan de profil.

A ) Perspective cavalière

C’est la perspective dont l’exécution est la plus simple ; elle convient très bien aux dessins rapides , mais elle déforme sensiblement l’objet représenté.

1°) Représentation d’une perspective cavalière d’un parallélépipède rectangle :

Principe :

Toutes les faces frontales sont dessinées en vraie grandeur.

Toutes les arêtes non frontales se dessinent suivant des fuyantes inclinées d’un même angle µ et sont réduites dans un rapport appelé :

« coefficient de réduction »

planper1

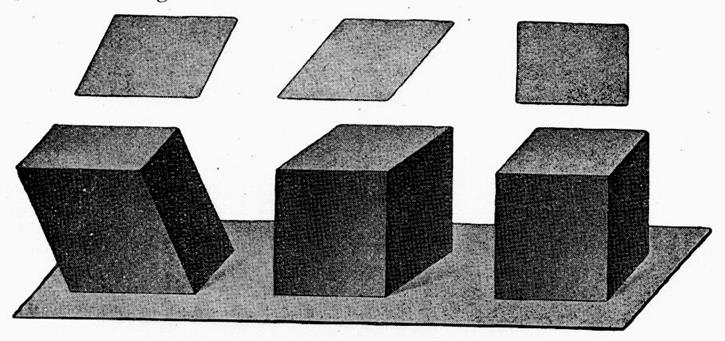
2°) Conventions de représentation des rectangles en perspective cavalière :

Rectangle vu verticalement de front	Rectangle vu horizontalement	Rectangle vu verticalement de profil

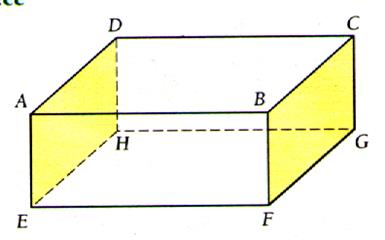
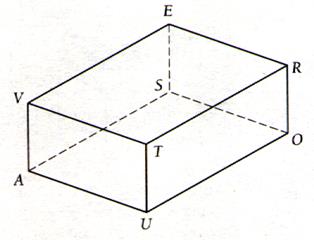
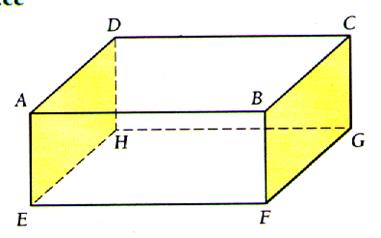
Remarques :

Un plan de front sera représenté par un rectangle ( ABCD)

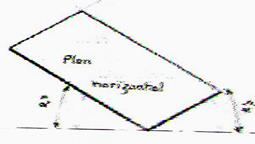
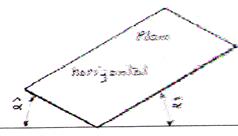
Un plan horizontal sera représenté par un parallélogramme tel ( EFCD ).

Un plan de profil sera représenté par un parallélogramme tel ( BHFC )

Attention : il ne faut pas oublier que les droites DE ; CF ; BH et CF étant des perspectives cavalières de quatre horizontales de bout , elle doivent être considérées comme des horizontales .l
B) la perspective dite « axonométrique » :

1°))La perspective axonométrique est d’exécution est la plus commode que la « cavalière »

( toutes les fuyantes sont inclinées de 30° par rapport à l’horizontale ) .

cette perspective s’utilise couramment pour les schéma de canalisation.

planperp

2°) Conventions de représentation des rectangles en perspective axonométrique :

Vu de gauche vers la droite		Vu de droite vers la gauche
Rectangle vu verticalement	Rectangle vu horizontalement	Rectangle vu horizontalement	Rectangle vu verticalement

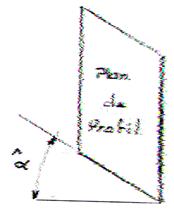
Remarques :

L’ angle a (alpha) vaut 30°.

Le plan frontal n’existe pas dans la perspective axonométrique.

Autres représentations :

TRAVAUX AUTO FORMATIF.

CONTROLE:

1°) Nommer deux perspectives linéaires utilisées en mathématique pour représenter des solides ?

EVALUATION:

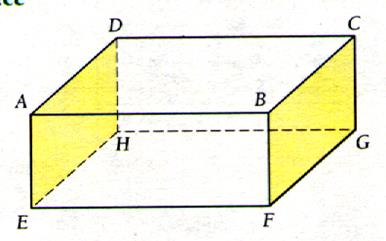
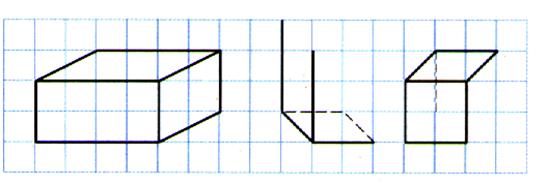
1°))Reproduire ces dessins et les compléter pour obtenir des dessins , en perspective , de parallélépipèdes rectangles.

Pour cela tracer les arêtes manquantes en trait plein ou pointillé.

spect1

2°) Sur une feuille ( 210 / 297 )divisée en deux parties ,dessiner une boite d’allumettes en perspective cavalière et perspective axonométrique.

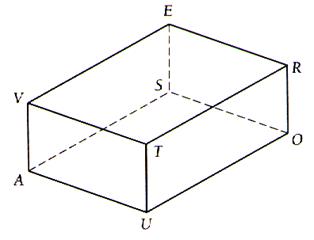
3°) Soit un prisme représenté en perspective :

Pour chaque cas dites quelle est la perspective que l’on a utilisé pour représenter ces prisme :

N° 1
N°2

Les solides dans l’espace

COURS

Représentation en perspective linéaire d’un prisme ( parallélépipède )

A ) en Perspective cavalière