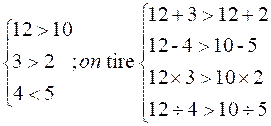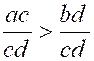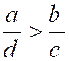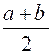RAPPELS :             Un nombre algébrique   « a » est plus grand qu’un nombre algébrique « b » , lorsque la différence  ( a – b ) ) est positive.

1°)  Définition :

·       On sait qu’une quantité « a » est dite « plus grande » ou « plus petite » qu’une quantité « b » , selon que la différence algébrique «  a – b » est « positive » ou « négative » . 

·       Toute quantité positive est dite « plus grande que zéro »  et toute quantité négative est  dite « plus petite que zéro » ;

·       L’inégalité «  a > b » peut donc s’écrire sous chacune des formes équivalentes suivantes : «  a – b > 0 » ; «  a= b + k² » ; «  a – b = k² » ; «  b < a » ; «  b – a < 0 » ; «  b = a – k² ».

On dit qu’un nombre « a »est supérieur à un nombre « b » si pour obtenir « a » il faut ajouter à « b » un nombre « positif » ou , ce qui revient au même, si la différence « a - b » est un nombre positif.

2 °)  Principes relatifs aux inégalités.

Des définitions et de la théorie des opérations fondamentales du calcul algébrique , on peut énoncer les principes  suivants.

Principes 1 : Si l’on a «  a > b »  et «  b > c » , on a aussi «  a > c » et l’on peut écrire   «  a > b > c »

Car les inégalités  «  a – b > 0 »  et «  b – c > 0 »  donne évidemment  «  ( a – b ) + ( b – c ) > 0 » ; d’où  «  a – c > 0 »

Principe 2 :  On peut , sans changer le sens d’une inégalité :

1°) Augmenter ou diminuer d’une même quantité les deux membres ;

2°) Multiplier ou diviser les deux membres par une même quantité positive.

3°) Elever à une même puissance les deux membres , s’ils sont tous deux positifs , ou extraire la racine « mième » des deux membres , s’ils sont tous deux positifs et qu’on ne considère que les racines positives.

Démonstration :

1°) Les trois inégalités «  a > b » ; «  a + m > b + m » ; « a- m > b – m »  signifie respectivement que les différences  «  a – b » ; «  ( a + m) – ( b + m) » ; « (a – m ) – ( b – m) sont toutes positives. Or , quelle que soit la quantité « m » ; ces trois différences sont égales entrent elles et , par suite , si l’une quelconque est positive , les autres le sont aussi. Les trois inégalités sont donc équivalentes. 

2°) Les inégalités «  a > b » , « a m > b m » , >  signifie respectivement que les différences « a – b » ; « am > bm » ;  -  sont positives. Or la seconde peut s’écrire «  m ( a – b » ; et la troisième  ( a – b) , et  si « m » est positif , ces produit ont toujours le signe de « a- b », par suite ,

si l’une des trois différences est positive, il en est de même des deux autres. Les trois inégalités sont donc « équivalentes ».

3°) Soient « a » et « b » deux quantités positives. On sait , par l’arithmétique, que suivant qu’une quantité arithmétique  « a » est supérieure  ou inférieure à une quantité « b » , les quantités arithmétiques «  a ⁿ »  et  «  »  sont supérieures ou inférieures aux quantités arithmétiques   «  b ⁿ »  et  «  »  .

Corollaires et complément d’informations .

On établira , sans difficulté ,  les propositions suivantes :

N°1 : Dans une inégalité, on peut transposer d’un membre dans l’autre un terme d’une inégalité, à condition de renverser le signe du terme.

N°2 : Si l’on multiplie ou divise par une même quantité négative les deux membres d’une inégalité , le sens de l’inégalité est renversé.

Ainsi, il y a équivalence entre les inégalités : «  a > b » et «  a ( - k²) < b ( - k²) » .

N°3 : Si les deux membres d’une inégalité sont négatifs , on peut les élever à une même puissance , en conservant ou en renversant le sens de l’inégalité suivant que cette puissance est « impaire » ou « paire ».

Exemple :   - 5 > - 7  donne :  ( - 5 )²  < ( - 7)² ;     ( - 5 )³   >   ( - 7) ³ ; etc……

Si les deux membres sont de signes différents , on peut les élever à une même puissance impaire , mais on ne peut rien dire des puissances paires.

Exemples .

 Les inégalités  « 5 > - 3 » ; «  5 > - 5 » ; «  5 > - 7 » donnent  « 5 ³ > ( - 3) ³ » ; «  5³  > (- 5) ³ » ; «  5³  > (- 7 ) ³ » ; mais on a  « 5² > ( - 3) ²  » ; «  5 ²  = (- 5) ²  » ; «  5 ²   <  (- 7 ) ²   » 

Remarques :

De l’inégalité «  a > b » , on ne peut conclure «  a ² > b² »  que si l’on sait, d’ailleurs , que les quantités « a » et « b » sont toutes les deux positives.

DE l’inégalité «  a ² > b² » ; on se gardera de conclure «  a > b » . Pour qu’on ait l’inégalité «  a ² > b² » ,il faut et il suffit  que « a » ne soit pas compris en « +b » et « -b »

Principe:

On peut , sans changer le sens d’une inégalité :

1°) Lui ajouter , membre à membre , une ou plusieurs autres inégalités de même sens qu’elle ;

2° ) En soustraire , membre à membre, une inégalité de sens contraire ;

3°) La multiplier par une inégalité de même sens , si les membres des deux inégalités sont positifs.

4°) La diviser par une inégalité de sens contraire, si les membres des deux inégalités sont tous positifs.

Exemples : Des inégalités 

Démonstration : 

1°) Les inégalités « a > b »  et «  c – d », ou  «  a – b > 0 » et   « c - d> 0 » ; donnent «  a – b + c – d > 0 » ; d’ où ( a + c ) – ( b + d ) > 0 »

2°)  Les inégalités « a > b »  et «  c < d », ou  «  a >  b  » et   « c >  d  » ; donnent «  a – b > 0 »   et  « c – d > 0 » ; d’ où «   a – b  + c – d > 0 ;   ( a-  d ) – ( b  - c ) > 0 »

3° )  Les inégalités « a > b »  et «  c < d »,si l’on multiplie les deux membres de l’une par « c » et les deux membres de l’autre par « b » , donnent  «  ac > bc » et « bc > bd » ; d’où  « ac > bd » .

4°) Les inégalités «  a > b »  et «  d < c » ou  «  a > b » et  «  c> d » , donnent «  ac > bd » comme on vient de voir ; en divisant les deux membres de cette égalité par la quantité positive « cd » , il vient :    ; ou  

Applications.

1°) Démontrer que la moyenne arithmétique  entre deux quantités positives inégales est supérieure à leur moyenne géométrique :

A la question  >  ?  on peut substituer cette autre question équivalente : «  a + b >  2  » ?

Ou cette autre : «  ( a + b )²  >  ( 2 ) ²  » ou  «  ( a + b )²  >  4  a b »   ou   «  a² - 2 ab + b² > 0 » ?  ou «  ( a + b ) ² > 0 » ?  Or    «  ( a + b ) ² > 0 »  . Donc «  >  »  

2°) Etablir l’inégalité «  x ⁵  + y ⁵ > x ⁴ y  - x y ⁴ »

Par décomposition en facteurs  , on a  «  x ⁵  + y ⁵ -  x ⁴ y  - x y ⁴  = x ⁴ ( x -  y )  -   y ⁴ ( x – y ) =  x ⁴  -  y ⁴ ( x – y ) =  ( x²  -  y² ) ( x + y ) ( x – y ) ² > 0 .

3°) Etablir que l’on a «  a² + b² + c² > ab + bc + ca » , sauf le cas «  a = b = c ».

On additionnera membre à membre  «  a² + b² > 2 ab » ; «  b² + c² > 2 bc » ; «  a² + c² > 2 ac » ; on observera que si «  a = b » ; « a² + b² = 2ab » ;……

4°) Laquelle de ces deux expressions : +  ou   est la plus grande ?

A la question +  >  ? on substituera  successivement les questions suivantes :

Est-ce que  (+ ) ²   >  10 ?

                   :    3 + 2  + 2 > 10 ?

                    :    + 2   > 5  ?

                    :   4 (  ) ²  >  25  ?

                     :   4 x 3 x 2    >  25  ?   ;  Or , on a 24 < 25   ; Donc   +  >

En effet , l’arithmétique donne les valeurs approchées :    = 1,4142 ,  = 1 , 7320  ,  = 3,1623