|
|
|
|
|
ENVIRONNEMENT du
dossier:
|
Index warmaths |
1°) Notions sur les opérations |
2°) les inégalités
triangulaires |
LES « INEQUATIONS » ( niveau 4 et 3 ):
-
Définitions et
- Les théorèmes et corollaires
(démonstrations)
|
TEST |
COURS |
Interdisciplinarité |
|
|
INEQUATIONS ( définitions) |
|
Inéquation :
On appelle « INEQUATION » une inégalité qui n’a lieu que pour
certaines valeurs attribuées à une ou plusieurs lettres appelées « inconnues ».
Exemples :
|
5x + 7 > 6x +13 |
Est une inéquation à
une inconnue. |
|
2x +5y -3 < 4x -3y +2 |
Est une inéquation à
deux inconnues. |
Toute inéquation est de la
forme : A
> B ou A < B
« A » est le premier
membre de l’inéquation et « B » le second membre.
On appelle
« solution » de l’inéquation tout ensemble de nombres qui, mis à la place des
inconnues, satisfait à l’inéquation.
Résoudre une inéquation, :
résoudre une inéquation c’est trouver
ses solutions.
Inéquations équivalentes : On dit que deux
inéquations sont équivalentes lorsqu’elles admettent les mêmes solutions.
Méthode de résolution d’une
inéquation :
Pour résoudre une inéquation, on
la transforme en « inéquations
équivalentes » jusqu’à ce qu’on obtienne une inéquation dont la résolution
est immédiate. Pour cela on utilise certains théorèmes qu’il faut démontrer.
THEOREMES :
THEOREME I :
Soit l’inéquation A > B et l’inéquation (2)
A + C > B + C obtenue en ajoutant une même expression algébrique
« C » aux deux membres de l’inéquation(1).
1°) Soit x = a une solution de l’inéquation (1). Dire que a est solution de l’inéquation (1) c’est dire que
les valeurs A’ et B’ que prennent A et
B lorsqu’on remplace « x » par
« a » sont telles que A’ >
B’
Pour « x = a », C prend une valeur C’. Puisque A’> B’ on a A ’ + C’ > B’ +
C’
Or A’ + C’ et B’ + C’ sont les valeurs que prennent les
deux membres de l’inéquation (2) lorsqu’on remplace « x » par « a ». L’inégalité précédente prouve que « a » est solution de l’inéquation (2).
2°) On démontrera de la
même façon que toute solution de l’inéquation (2) est solution de
l’inéquation(1) (qu’on peut considérer comme déduite de (2) en ajoutant aux
deux membres la même expression « -C »
Donc les inéquations
(1) et (2) sont équivalentes, c’est à dire :
Théorème : On
obtient une inéquation équivalente à une
inéquation donnée en ajoutant à ses deux membres une même expression
algébrique.
Remarque 1 : la
démonstration précédente suppose qu’on peut calculer la valeur C’ et C pour
« x = a » .En particulier, il en sera toujours ainsi
si « C » est un polynôme.
Remarque 2 : Nous
avons fait la démonstration précédente en supposant qu’il s’agissait
d’inéquation à une inconnue. On raisonnerait de la même façon pour une inéquation
à plusieurs inconnues et on serait conduit au même résultat.
COROLLAIRE :
Soit l’équation :
(1)
2 x + 8 < 9x - 7
Ajoutons aux deux
membres l’expression « -2x ».On obtient l’inéquation
équivalente :
(2) 8 < 9x - 7 - 2x
C’est deux inéquations
ne diffèrent que par le terme « 2x » qui ,
dans l’équation (1) est dans le premier membre précédé du signe « + »
et dans l’inéquation (2) dans le second membre précédé du signe « - » . Donc :
(à
savoir)
On obtient une inéquation
équivalente à une inéquation donnée en faisant passer un terme d’un membre dans
l’autre et en changeant son signe.
THEOREME II
.
Soit l’inéquation (1)
A > B
Et l’inéquation (2) m A > m B obtenue en multipliant les deux membres de
l’inéquation (1) par un même nombre
« m ».
Ces deux inéquations sont respectivement équivalentes
à :
( 3) A - B > 0
et m A - m B > 0
c’est à dire (4) m ( A -
B) > 0
1°)
Toute solution de (3) donne à A -
B une valeur positive. Elle sera donc solution de (4) si « m » est positive.
2°) Réciproquement,
toute solution de l’inéquation (4) donne au produit m(A-B)
une valeur positive.
Si « m » est
positif elle rend A - B positif et est
donc solution de l’inéquation (3)
Par suite
, si m > 0 les inéquations (1)
et (2) sont équivalentes.
On démontrera de même
que si « m » est négatif, l’inéquation (1) est équivalente à :
m A < mB
D’autre part , comme on passe de l’inéquation (2) à l’inéquation (1)
en divisant les deux membres par « m », on est conduit à l’énoncé
suivant :
Théorème . On obtient une inéquation équivalente à une inéquation
donnée en multipliant ou divisant ses deux membres par un même nombre
« POSITIF ».
On peut aussi les
multiplier ou les diviser par un même nombre « NEGATIF » en changeant
le sens de l’inéquation.
CAS PARTICULIER. On
obtient une inéquation équivalente à une inéquation donnée en changeant les signes de ses deux membres et en
changeant son sens.
Cela revient en effet à
multiplier les deux membres par « -1 ».
APPLICATION :
Soit
l’inéquation :
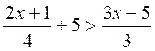
Multiplions les deux
membres par 12 . On obtient l’inéquation
équivalente :
3
( 2 x +1) + 60 > 4 ( 3x - 5)
dans laquelle les deux membres n’ont pas de
dénominateur. On dit qu’on a chassé les dénominateurs.
Remarque. De même que
pour le théorème I , on verra que le théorème II est
applicable aux inéquations à plusieurs inconnues.
CONTROLE :
1°) Qu’appelle - t on Inéquation ?:
2°) Que cherche -t-on lorsque l’on veut résoudre une
inéquation ?
3°) Quand dit
- on que des Inéquations sont équivalentes : .
4°) Compléter la phrase :
Pour résoudre une inéquation, on
la transforme en « ……………………. »
jusqu’à ce qu’on obtienne une inéquation dont la ………………………...
5°) Qu’utilise - t- on pour résoudre une inéquation ?(que faut-il
connaître ?)
6°) Citer les 2 théorèmes qui permettent de
résoudre les inéquations.
EVALUATION
|
Les inégalités suivantes sont – elles vraies ? |
Prouvez par un calcul : |
|
- 4 < -3 |
|
|
-2 > -7 |
|
|
-2 < 0 |
|
|
-5 < 1 |
|
Rien
d’autre pour l’instant ! : voir >>> INEQUATION
DU PREMIER DEGRE A UNE INCONNUE.