|
Auteur :
WARME R.
Document
« élève »
|
|||||||||||||||||||||||||||||||||||
|
NOM : ……………………………… |
Prénom : ………………………….. |
Classe :………………….. |
|||||||||||||||||||||||||||||||||
|
Année scolaire : ……………………… |
Dossier
pris le : ……/………/……… |
Validation
de la formation : O -
N Le : …………………………………….. Nom
du formateur : …………………… |
|||||||||||||||||||||||||||||||||
|
ETABLISSEMENT :
………………………………………….. |
|||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||
|
Travaux
spécifiques sur les angles : |
|||||||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||
|
Travaux
spécifiques sur les conversions d’unités d’aire. |
|||||||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
Titre |
|||||||||||||||||||||||||||||||||||
|
N°14 |
les UNITES DE LONGUEUR ; D' ANGLE ; D' AIRE. |
||||||||||||||||||||||||||||||||||
|
CHAPITRES |
|||||||||||||||||||||||||||||||||||
|
Info plus !!!!!sur les conversions de longueur. |
|||||||||||||||||||||||||||||||||||
|
III ) Unité d'aire : le mètre carré ( symbole : m² )
et « mesure
agraire » |
Info plus !!! sur l'aire et le système métrique. |
||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||
|
1°) Définition du « mètre »: |
|||||||||||||||||||||||||||||||||||
|
L’unité
de mesure de longueur s’appelle le
« mètre » , symbole
« m ». i l’outil
de mesure par comparaison est le mètre
étalon : est la longueur , à la température de 0
degré , du prototype international en platine iridié, qui a été sanctionné
par la Conférence générale des Poids et Mesures tenue à Paris en 1889 , et qui a été déposé au pavillon de Breteuil , à Sèvres. Entre
1889 et 1983 de nombreuses définitions
, plus précises , ont été
données au mètre . depuis 1983 on a
remplacé la dernière définition
par une définition encore plus précise
: le mètre est la longueur du trajet parcouru dans le vide par la lumière
pendant une durée de : |
|||||||||||||||||||||||||||||||||||
|
|
|
seconde. |
|||||||||||||||||||||||||||||||||
|
2°) Les
multiples et sous multiples du mètre . |
|||||||||||||||||||||||||||||||||||
|
Sous multiples du mètre : En divisant le mètre par dix (on obtient 10 / 10ème
de mètre , soit 10 morceaux de 1/10ème de mètre ) ,puis
on divise par 10 un 1/10ème de ces morceaux de mètre ( on
obtient des morceaux de longueur qui
mesure 1/100ème de mètre) ;
puis à nouveau par dix l un des morceaux précédents et ainsi de suite ( les morceaux deviennent de plus en plus petits , au point de ne plus
les voir à l’œil nu , on prendra des
microscopes ),on obtient les
catégories de sous multiples . Multiple du mètre : On obtient les multiples du mètre en
multipliant par dix le mètre , puis
par dix la longueur précédente ; puis à nouveau par dix la
longueur précédente et ainsi de suite
( les longueurs deviennent de plus en plus grandes , au point de ne plus pouvoir les
mesurer directement avec un
instrument . |
|||||||||||||||||||||||||||||||||||
|
3°)
Noms des multiples et sous-multiples du mètre : |
|||||||||||||||||||||||||||||||||||
|
Pour exprimer des longueurs
, on utilise les multiples du mètre et les sous - multiples du mètre. |
|||||||||||||||||||||||||||||||||||
|
Unités |
Symboles |
Valeur en mètre ( équivalence ) |
|||||||||||||||||||||||||||||||||
|
Kilomètre |
km |
1 km = 1 000 m |
|||||||||||||||||||||||||||||||||
|
Hectomètre |
hm |
1 hm = 100 m |
|||||||||||||||||||||||||||||||||
|
Décamètre |
dam |
1 dam = 10 m |
|||||||||||||||||||||||||||||||||
|
Mètre |
m |
1 m |
|||||||||||||||||||||||||||||||||
|
Décimètre |
dm |
1 dm = 0,1 m |
|||||||||||||||||||||||||||||||||
|
Centimètre |
cm |
1 cm = 0,01 m |
|||||||||||||||||||||||||||||||||
|
Millimètre |
mm |
1 mm = 0, 001 m |
|||||||||||||||||||||||||||||||||
|
Micron |
(mu) m |
1 m = 0 , 000 001 m |
|||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||
|
4°) Extrait du tableau
de conversion des unités de longueur |
|||||||||||||||||||||||||||||||||||
|
Nous fixons notre
attention sur les unités les plus
utilisées dans la vie quotidienne : i Dans la vie professionnelle on
choisi une unité de base : elle est le mm pour l’ébéniste
, le cm pour le maçon et le micron pour le mécanicien , le physicien
utilisera d’autres unités . Pour convertir les
unités de longueur , on utilise le tableau
simplifié suivant : |
|||||||||||||||||||||||||||||||||||
|
Km ; hm ;
dam ;et m
appartiennent à la Partie entière |
Dm ; cm ; mm appartiennent à la partie décimale |
||||||||||||||||||||||||||||||||||
|
km |
hm |
dam |
m |
dm |
cm |
mm |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||
|
5°)
Exploitation du tableau , procédure : |
|||||||||||||||||||||||||||||||||||
|
La démarche ( I ) doit vous servir à comprendre le déplacement de la
virgule , la procédure II est celle qui faut retenir . |
|||||||||||||||||||||||||||||||||||
|
I ) démarche explicative sur la méthode de
conversion en utilisant le tableau non simplifié : |
œ |
||||||||||||||||||||||||||||||||||
|
( pour la
compréhension) ;Entre
chaque unité il devrait exister une « sous - colonne » dans laquelle on place ou se déplace la
virgule, cette « sous colonne » diminuera en « largeur »
, pour ne devenir qu’un trait vertical
, dans la forme simplifiée du tableau . Alors la virgule se déplacera
sur ce trait vertical.
1°) construire le tableau
suivant : |
|||||||||||||||||||||||||||||||||||
|
km |
|
hm |
|
dam |
|
m |
|
dm |
|
cm |
|
mm |
|
0,1 mm |
0,01 mm |
0,001 mm |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
2°) placer la virgule dans la sous
-colonne se trouvant à droite de
l'unité donnée: |
|
||||||||||||||||||||||
|
km |
|
hm |
|
dam |
|
m |
|
dm |
|
cm |
|
mm |
|
|
|||||||||
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
3°) ranger les chiffres en respectant l'ordre ; ( 1 chiffre par colonne unité ); compléter avec des zéros. |
|
||||||||||||||||||||||
|
km |
|
hm |
|
dam |
|
m |
|
dm |
|
cm |
|
mm |
|
|
|||||||||
|
4 |
|
5 |
, |
3 |
|
2 |
|
6 |
|
0 |
|
0 |
|
|
|||||||||
|
4°)
déplacer la virgule ; la positionner
dans la sous- colonne de droite
de l'unité demandée. |
|
||||||||||||||||||||||
|
km |
|
hm |
|
dam |
|
m |
|
dm |
|
cm |
|
mm |
|
|
|||||||||
|
4 |
|
5 |
|
3 |
|
2 |
|
6 |
|
0 |
, |
0 |
|
|
|||||||||
|
|
|
|
, ®®®®® On déplace la virgule ! ®® |
|
|
|
|||||||||||||||||
|
5 °) Conclusion : 45,326 hm = |
|||||||||||||||||||||||
|
4 |
|
5 |
|
3 |
|
2 |
|
6 |
|
0 |
, |
0 |
|||||||||||
|
Soit : 453260,0
cm = 453260
cm Si
l'on veut exprimer le résultat dans une autre unité ,
il suffit de déplacer la virgule vers la gauche, ou vers la droite dans le
tableau . |
|||||||||||||||||||||||
|
km |
|
hm |
|
dam |
|
m |
|
dm |
|
cm |
|
mm |
|||||||||||
|
4 |
|
5 |
, |
3 |
|
2 |
|
6 |
|
0 |
, |
0 |
|||||||||||
|
|
|
|
¬¬
¬¬¬¬¬¬¬¬¬¬¬¬¬¬¬¬
|
|
|||||||||||||||||||
|
4 |
|
5 |
|
3 |
, |
2 |
|
6 |
|
0 |
|
0 |
|||||||||||
|
On
lit directement dans le tableau :
453 260 cm = 453,26 dam ;
autre exemple : 45,326 hm
= 4532,6 m; …………. |
|||||||||||||||||||||||
|
II )
Procédure à retenir : |
œ |
||||||||||||||||||||||
Exploitation du tableau simplifié , la « sous
colonne » qui sépare les
unités à disparu !. ce tableau est couramment utilisé , pour
effectuer une conversion de longueur: Il est à savoir dessiner sur le papier
pour ensuite ne l’avoir que dans la « tête ».
Application :
convertir 37,24 dam en
dm ou 37,24 dam = …? ……..dm
Procédure : pour effectuer la conversion il suffit de suivre la
procédure suivante.
A) tracer
le tableau de conversion sur la
feuille :
|
km |
hm |
dam |
m |
dm |
cm |
mm |
|
|
|
|
|
|
|
|
B) placer
dans le tableau la « grandeur donnée » ( ici des dam )
: On respectera l’ordre suivant
- b - 1
Placer la virgule du « nombre donné » sur le trait vertical "droit" de
l'unité donnée.
(ici la virgule se trouve
sur le trait séparant
les unités "dam" , et
"m" )
|
km |
hm |
dam |
m |
dm |
cm |
mm |
|
0 |
3 |
7 ® |
¬ 2 |
4 |
0 |
0 |
|
|
|
Emplacement de la virgule |
|
|
|
|
b- 2
Placer les chiffres du nombre dans en respectant l ' ordre donné ;
mettre un chiffre par colonne ,
b - 3
Remplir les cases vides de "zéro". ( 0372400)
ila "grandeur"
à convertir est maintenant placée dans le tableau il ne reste plus qu ' à
effectuer la conversion dans
l'unité demandée.
C) faire
la conversion :
- c- 1 ) Déplacer la virgule ; la mettre sur le trait vertical
"droit" de l' unité "demandée " (ici
sur le trait vertical entre dm et
cm )
|
km |
hm |
dam |
m |
dm |
cm |
mm |
|
0 |
3 |
7 |
2 |
4 ® |
¬ 0 |
0 |
|
|
|
|
Nouvel emplacement de la virgule |
|
||
- c- 2 )
Reporter le résultat , (lu dans
le tableau : 03724,00 dm soit
3724 dm )
i*remarque : dans le tableau une colonne est limitée
par 2 traits verticaux
, l'un à droit l'autre à
gauche . La virgule est dite
« flottante » ;elle se trouve toujours sur
le trait vertical "limite droite" de l 'unité concernée.
† Activités uv:
1 - Placer , dans le tableau
les longueurs suivantes :
2,346 km ; 12, 874 m ; 5342 mm ; 465 cm et 74 dm
dans le tableau de conversion :
|
km |
hm |
dam |
m |
dm |
cm |
mm |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Solution à
la fin du cours.:
† Activités v: (en réutilisant le tableau ci - dessus )
Faire
les conversions :
2,346 km = ? ………………….. dm =
……………………..? m
12, 874 m
= ? …………………. dm
=
?...............................
mm
5342 mm = ?
………………….. m = ? …………………….
dm
465 cm = ?
……………………..mm = ?............................... m
74 dm = ? ……………………….. hm
= ? …………………. mm
Corrigé
à la fin du cours !!!
Travaux
spécifiques : niveau VI et V:
|
Dossier 24 - 25 : |
Dossier 38 : |
Dossier 54- 55 : |
|
i19 instruments.
i29 les angles ; i39 Résumé : Vue en collège . |
|
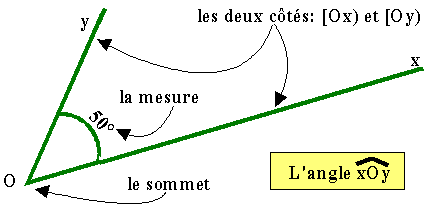
Définition : Un angle a un sommet et deux côtés. La mesure d'un angle ne dépend pas de la longueur de ses côtés. Elle dépend de l'écartement des côtés. Les unités de mesure sont le degré(°), le grade(gr) et le radian(rd). L'outil de mesure est le rapporteur.
|
|
Les unités utilisées pour graduer des rapporteurs
servant à mesurer des angles sont le degré et le grade :
Le grade « utilise » comme
système de numération , le système décimal . ( base 10)
Le degré « utilise » comme système de numération , le système sexagésimal . (base
60)
Dans l’exemple ci dessus : Le même angle mesure 50 degrés ou
55,56 grades , suivant que l’on
mesure l’angle avec un rapporteur gradué
en degrés ou en grades.
( remarque :
si l’on connaît une mesure en degré il
est possible de convertir , par calcul , la mesure en grades , pour cela voir
le chapitre ci dessous .)
L'instrument
de mesure d'un angle est le rapporteur . d'angle (peut - être
gradué en degré et en grade) :
Le rapporteur d'angle gradué en degrés et le plus utilisé.
|
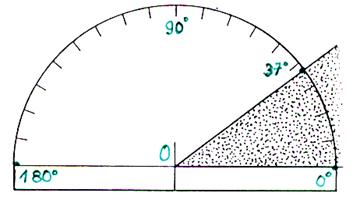
La mesure est obtenue en
plaçant le rapporteur le point O de l’angle coïncident avec le point O du
rapporteur. La demi droite O x placer sur la droite O
0° du rapporteur. |
Lecture de
la valeur de l’angle : la demi – droite
O y coupe l’arc gradué du rapporteur. La mesure 37 ° de cet arc est la mesure de l’angle |
Remarque : un demi - cercle décrit un arc
de 180° ; un cercle décrit un arc de 360°
Pré
requis: revoir la leçon sur la fraction d’heure ( durée)
|
b ) Unité d’angle :
Le degré et le système sexagésimale
|
|
— L’unité principale : le degré
|
|
— La mesure de l'angle est , en général,
exprimée en degrés
— Le degré utilise le
système de numération dit : sexagésimal
( base 60 )
—Dans un degré il y a 60
minutes, et dans une minute il y a 60
secondes
on en déduit que Dans un degré il y a 60 fois 60
secondes soit 3600 secondes
—Symboles :
|
Unité |
Degré |
Minute |
Seconde |
|
Symbole |
… ° |
……’ |
…….’’ |
|
Commentaire sur le symbole : |
C’est un « rond » placé
en exposant à droite du nombre. |
C’est une « apostrophe » placée
à droite du nombre. |
C’est une « double
apostrophe » placée en en exposant
à droite du nombre. |
Ainsi « 37
degrés 24 minutes et 15 secondes »
se traduit : 37° 24’ 15’’
|
c ) Une autre unité d’angle : le grade |
La mesure de l'angle est aussi exprimée en "grade" , alors un
angle droit mesure 100 grades
Pratiquement
,pour toutes les opérations topographiques
, on utilise le grade et ses sous –multiples.
|
d) Convertir des « degrés » en
« grades » et vis versa . |
Si "x" est la mesure d'un angle exprimée en degré et "y" la mesure
correspondante exprimée en grades , on a ![]() =
= ![]() . (info plus!!! sur les calculs )
. (info plus!!! sur les calculs )
Les mesures des angles exprimées en
degrés et en grades sont proportionnelles à 90 et à 100 respectivement
.
† exemple 1 :
Q : Passer d'une mesure exprimée en
"degré" et l’exprimer en "grade".
|
Degrés |
Calculs : |
Grades |
|
67° |
|
= 74,45 gr. |
† exemple 2
:
Q : Passer d'une mesure exprimée en "grade" et l’exprimer
en "degré" :
|
Grades |
Calculs : |
degrés |
|
67 gr |
|
=
60,3 ° |
|
e) Expression d’une valeur angulaire
exprimée en « degré ,minute , seconde »
(dite écriture sexagésimale ) en
écriture décimale : |
Remarque :
On peut
exprimer la valeur d’ un angle
en degré dans le système décimal ou le système sexagésimal :
Pour ce qui concerne la
mesure de la durée du temps qui passe on
peut ,par exemple, dire
que « 3 heures et
demi » s’écrira
« 3,5 h » , en écriture décimale »
Et dire
que « trois heure est demi »
s’écrira 3 h 30 minutes en
écriture sexagésimale
Pour ce qui concerne la mesure des angles , on utilisera la même démarche de penser : on peut ,par exemple, dire que « 3 degrés et demi » s’écrira « 3,5 ° » , en écriture décimale » ;
Et dire
que « trois degrés est demi » s’écrira 3 degrés 30 minutes en écriture sexagésimale ; ou en écriture
symbolique : 3 ° 3° ‘
=
écriture Degré et
écriture décimale :
Exemples d ‘ écriture numérique d'un angle
exprimé en degré en utilisant l'écriture
décimale .
Exemple 1 :
21,6° = On décompose : 21,6° = 21 ° +
0,6 ° = se
décompose en 21° + ![]() ° ;
° ;
Exemple 2 :
53,79 ° = ? On décompose : 53,79° = 53° + 0,79
° ; se décompose en 53° +![]() ° ou
53° +
° ou
53° +![]() °+
°+![]() °.
°.
On
décompose
=Degré et
« écriture sexagésimale » :
Ecriture numérique d'un angle exprimé en degré en
utilisant le
système sexagésimal .
Dans le système sexagésimale on exprime la mesure d'un
angle : en degrés , minutes et secondes .
|
Unités |
Symbole |
Equivalence |
Remarque : |
|
Degré |
° |
1° =
60 ' = 3 600" |
Dans
un degré il y a 60 minutes. |
|
Minute |
' |
1 ' = |
Dans
une minute il y a 60 secondes |
|
Seconde |
" |
1" = |
Dans
une seconde il y a 10/10ème ou 100/100ème de seconde . |
Exemple : 37° 24’ 15’’ se traduit
« 37 degrés 24 minutes et 15 secondes »
=Il faut : Savoir effectuer le
passage d'une écriture décimale
en écriture sexagésimale et vis versa . (Info plus!
Sur le système sexagésimal !) :
a)
passage d'une écriture décimale en écriture sexagésimale :
Procédure :
il suffit de multiplier la valeur décimale exprimée en degré par 60' .et la
valeur décimale de minute par 60".
|
Dit aussi : nombre décimal |
On « multiplie par 60 » Le nombre décimal |
Valeur sexagésimale |
||||||
|
0,1° |
|
0,1 |
||||||
|
0,5° |
|
0,5 |
||||||
|
Lorsque
le nombre possède une partie entière , on a deux
possibilités pour convertir soit 2
solutions pour exprimer en valeur décimale : |
||||||||
|
Solution
1 : 13,5 ° |
on multiplie uniquement le nombre décimale par
« 60 » |
13,5 |
||||||
|
Solution
2 : 13,5 ° |
On
décompose le nombre décimal ; on ne touche pas à la partie
entière ! on multiplie uniquement la partie décimale par
« 60 » : 13,5 ° = 13°
+ 0 ,5 ° |
13° +
0,5° 13 ° + 30 ‘ = 13°30' |
||||||
|
On
peut ainsi exprimer ; indifféremment ; 13,5° en minutes : 13, 5°
= 810 ‘ ou en « degrés et minutes » 13, 5°
= 13° 30’ On
remarquera que 810
: 60 = 13 ;
et il reste « 30 » , (ce qui peut aider pour de vérifier si
le calcul est exact.) |
||||||||
|
On procédera de même pour
les calculs qui concernent les « minutes » et « secondes » : |
||||||||
|
Exemple 1:
Transformation
de l’écriture 12,5 mn ( en décimal) en écriture 12’30’’ (en sexagésimal) : |
||||||||
|
On
décompose : 12,5
minutes = 12’ + 0,5 ’ |
|
On
conserve les 12 minutes ; on multiplie 0,5 par 60 ( 0,5´
60 = 30). Conclusion :
12,5 ‘ en « décimal »
donne 12 minutes et 30 secondes ( en sexagésimal) |
||||||
|
Exemple 2:
Transformation
de l’écriture 29,67 ° ( en décimal) en écriture 29°40’ 12’’ (en sexagésimal) |
||||||||
|
Solution 1 : On décompose :
29,67° = 29° + 0,67° Solution
2 : |
|
On
conserve les « degrés » et
on calcule pour transformer les 0,67 de minute en secondes. 0,67 ' On
aurait pu calculer le total de minutes : 29,67° |
||||||
|
Ainsi : 29,67° = 29°
+ 40,2' ( le résultat n’est pas satisfaisant : il
faut
transformer les 0,2 minute en secondes ) |
||||||||
|
2°) on décompose : 40,2 ' = 40' + 0,2 ' |
40,2 ' = 40' + 0,2 ' soit 0,2 soit 40' + 0,2 '
= 40' + 12 " |
|
||||||
|
On peur donc conclure que : 29,67° =
29° 40 ' 12 " |
||||||||
|
On retiendra : Pour passer
d’une écriture décimale à une écriture
sexagésimale , il faut conserver la partie entière « en
degrés » et il suffit de
multiplier la partie décimale exprimée en degré par 60' .( pour obtenir des
minutes ) et de multiplier la partie
décimale des minutes ( si elle existe) par 60" pour obtenir
« des secondes » . |
- b) passage
d'une écriture sexagésimale en écriture décimale.
Procédure de calcul : On garde la partie entière en degré
, on multiplie les minutes par ![]() .et
les secondes par
.et
les secondes par ![]() ; (ou
; (ou ![]() fois
fois![]() )
)
|
Valeur sexagésimale |
On
multiplie les minutes par |
conversion |
|
6' |
6 |
0,1' |
|
13° 30' |
13° + 30 |
13° + 0,5 ° = 13,5 ° |
|
62° 15' |
62° + 15 |
62° + 0,25° = 62,25 ° |
|
Valeur sexagésimale possédant des :
° ; ' ;
" |
conversion |
|
|
46° 22' 45" |
46° = 46° 22 ' = 22 45 " = 45
|
46° + ( 0,37
+ 0,01) = 46,38° |
|
On retiendra : Pour passer d’une écriture sexagésimale à une écriture décimale , il faut
conserver la partie entière « en degrés » et il suffit de diviser les minutes par 60 (pour obtenir une nombre décimal de degré de la forme 0,….) et de diviser les secondes par
3600 (, pour obtenir un nombre décimal de la forme
0,0 )…. Le résultat est la
somme des trois nombres : ….. degrés + 0,…+ 0,0… |
|
Pour en savoir plus : il
faut faire des opérations avec des
nombres exprimés dans le système
sexagésimal .Ce type de calculs est utilisé avec les angles
, mais aussi avec les heures . et dans les coordonnées d’un point sur
la sphère terrestre. On réinvestira ces connaissances
pour les calculs sur les vitesses moyennes , les distances ; … |
1°)Les heures :calculs dans le système sexagésimal . 2°)Les angles opérations dans le même système.. 3°)
Géographie : latitude et
longitude. |
Nous traitons dans ce cours des unités « d' aire »
et non du calcul d’aire !!!!!!. ( le calcul de l'aire d'une surface se fera par la suite : cours N°16 ).
|
a)
Définitions et remarques |
= " AIRE " :
On donne le nom d ’ « aire » à
l’étendue d’une surface.
La valeur donnée à l ’ « aire »
est le nombre de carrés entiers, de
dimensions définies ,
contenus à l’intérieur d’un contour
d’une figure géométrique.
Ainsi :
les outils de mesure par comparaison sont des carrés en matériau solide ( bois , papier ;….):
|
Le carré de |
1 m de côté |
1 dm de côté |
1 m de côté |
1 mm de côté |
|
est appelé |
1 mètre carré |
1 décimètre carré |
1 centimètre carré |
1 millimètre carré |
|
On le note symboliquement : |
.m² |
.d m² |
.cm² |
.mm² |
Exemple :
Pour mesurer l’aire d’une
pièce il a fallu « couvrir » la surface par : 2 3 m² + 8
dm² + 5 cm² + 2 mm² que l’on écrira : 23 , 8 5 2 m ²
="SURFACE" :
On appelle « surface » la portion de plan située à l’intérieur d’une
ligne fermée.
Les surfaces élémentaires de bases sont : le rectangle ; le
carré , le triangle , le cercle et le trapèze . ( le trapèze peut se décomposer en
association de figures élémentaires).
Nous pouvons donc remarquer que d’après les
définitions que le mot « surface » et « aire » ne sont pas synonymes .
Le
mot « surface » évoque l’idée de forme ,
tandis que le mot « aire » est pris dans le sens de « grandeur » à mesurer.
Remarque :si deux surfaces sont superposables , elles sont égales ,
il est évident que les aires sont aussi égales.
= Obtention de la valeur de l’aire d’une surface
.
Pour obtenir l’aire d’une
surface ; plusieurs solutions sont possibles :
- En utilisant la méthode du carrelage. Il faut avoir à sa disposition des carrés de 1m² ;
1dm² ; 1cm² ; ….
- En traçant sur le sol un
quadrillage et
compter les carreaux .
- En faisant un plan « à l’échelle » sur feuille , et en traçant un
quadrillage et compter les carreaux.
- En faisant un ou des calculs
.
Voir cas à cas :
►Si la surface est de forme élémentaire simple on applique la formule.
►Si la figure est de forme complexe , non curviligne , il faut découper la
figure complexe en
figures élémentaires
simples ;on
calcule chaque surface élémentaire , et on fera la somme des aires .
►Si la figure est complexe et curviligne , il faut découper la figure complexe en figures élémentaires
simples ;on calcule chaque surface
élémentaire , et on fera la somme des aires
|
b) L '
unité d'aire : |
L'unité
d'aire dans le système métrique est le "mètre carré" ; symbole
« m² »
L'unité
d'aire « agraire » dans le
système métrique est l ‘ " are
" ; symbole « a »
Le mètre carré ( m2
) est la superficie contenue dans un carré de 1 mètre de côté .
|
c) Les multiples et sous multiples de l’ unité d’aire m²
: |
L'instrument de mesure ( par comparaison) est un carré de 1 mètre de côté.
Pour les aires « plus petites » on prendra des carrés de dimensions
inférieures, appartenant aux sous - multiples du mètre. ( le dm² ;
le cm² ; le mm² ). Cette mesure par comparaison consiste à recouvrir de
"petits carrés" la surface à mesurer .
|
|
Unités multiples du m2 |
Unité « référente » |
Unités sous-
multiples du m2 |
||||
|
"Carrés" unités ® |
km2 |
hm2 |
dam2 |
m2 |
dm2 |
cm2 |
mm2 |
|
Lg. des côtés de ces carrés
® |
1 km de côté |
1 hm de côté |
1 dam de côté |
1m de côté |
1dm de côté |
1cm de côté |
1mm de côté |
|
d) La
numération des unités d’aire |
Les
unités d’aire suivent la loi
« centésimale » , c’est à dire qu’elles sont
de cent en cent fois plus grandes ou plus petites.
Ainsi il faut 100 m2 pour faire 100 dam2 ; et il
faut 100 dam2 pour faire 1 hm2 ;..
Dans le décimètre
carré : (symbole : dm²) il y a 100 cm² ; ……
Chaque « colonne unité » du tableau contient 2 sous colonnes .
|
Nom |
Symbole |
Correspondance en m² en
valeur décimale et sous forme de puissance de 10. |
|
|
Kilomètre carré |
Km ² |
1 km
² =1 000 000 m ² = 1 ´ 10 6 m ² |
|
|
Hectomètre carré |
h m² |
1 h m ² = 10 000 m ² = 1 ´ 10 4 m ² |
|
|
Décamètre carré |
da m² |
1da m² = 1 00 m ² = 1 ´ 10 2 m ² |
|
|
Mètre carré |
m² |
1 m² = 1´ 10 0 m ² |
|
|
Décimètre carré |
d m² |
1 d m² =
0 , 01 m2 = 1 ´
10 -2 m ² |
|
|
Centimètre carré |
c m ² |
1 c m ² =
0, 0001 m2 = 1 ´ 10 -4 m ² |
|
|
Millimètre carré |
m m² |
1 m m
² = 0 , 000 001 m2 = 1 ´
10-6 m ² |
|
|
|
|
||
|
e) Le tableau de conversion : |
|||
La démarche ( I ) doit vous servir à comprendre le déplacement de la
virgule , la procédure II est celle qui faut
retenir .
|
I ) démarche
explicative sur la méthode de conversion
en utilisant le tableau non
simplifié : |
œ |
Tableau type
non simplifié :.( à gauche de la virgule se trouve
l'unité choisie (ou désignée) à droite de la virgule se trouve la partie
décimale de l'unité choisie ou désignée )
Pour « apprendre » à utiliser le tableau on considérera qu’il existe des colonnes réservées à la "virgule", elles séparent les « unités », dans ces colonnes se déplace la virgule., par la suite la colonne se rétrécira en épaisseur , et son épaisseur sera réduite à un trait vertical , sur lequel se déplace la virgule.
|
km2 |
|
hm2 |
|
dam2 |
|
m2 |
|
dm2 |
|
cm2 |
|
mm2 |
|
|||||||
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f ) Application :
Convertir
3,574 dam² en dm ² ; on fait dans
l’ordre :
- 1°) on
place la virgule dans le tableau: ( entre dam ² et m²)
|
km2 |
|
hm2 |
|
dam2 |
|
m2 |
|
dm2 |
|
cm2 |
|
mm2 |
|
|||||||
|
|
|
|
|
|
|
|
|
' |
|
|
|
|
|
|
|
|
|
|
|
|
- 2°) on
place les chiffres :
|
km2 |
|
hm2 |
|
dam2 |
|
m2 |
|
dm2 |
|
cm2 |
|
mm2 |
|
|||||||
|
0 |
0 |
|
0 |
0 |
|
0 |
3 |
' |
5 |
7 |
|
4 |
0 |
|
0 |
0 |
|
0 |
0 |
|
-3°) on
déplace la virgule :
|
km2 |
|
hm2 |
|
dam2 |
|
m2 |
|
dm2 |
|
cm2 |
|
mm2 |
|
|||||||
|
|
|
|
|
|
|
0 |
3 |
|
5 |
7 |
|
4 |
0 |
, |
0 |
0 |
|
0 |
0 |
|
|
|
|
|
|
|
|
|
|
' |
®®®®®®®® |
|
|
|
|
|
|
|
||||
-
On reporte le résultat
|
dam2 |
|
m2 |
|
dm2 |
|
|||
|
0 |
3 |
|
5 |
7 |
|
4 |
0 |
, |
- 4°)
Conclusion : 3,574 dam² = 35 740 dm²
|
II ) Procédure à retenir sur l ’ exploitation du tableau pour effectuer une
conversion: |
œ |
Dans le tableau type
simplifié ( à savoir reproduire ), la virgule se
déplace sur le trait vertical séparant les colonnes .
Exemple :
faire la conversion 37,24
dam ² = …? ……..dm²
Procédure : il faudra
respecter l’ordre chronologique suivant
1°) Tracer le tableau et placer dans le tableau la grandeur donnée:
|
km2 |
hm2 |
dam2 |
m2 |
dm2 |
cm2 |
mm2 |
||||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2°) placer la virgule du
nombre donné sur le trait
vertical "droit" de l'unité donnée.
(sur le
trait séparant "dam² , et "m²" )
|
Km2 |
hm2 |
dam2 |
m2 |
dm2 |
cm2 |
mm2 |
||||||||
|
|
|
|
|
|
® |
← |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3°) placer les chiffres du nombre dans en
respectant l '
ordre donné ; mettre deux chiffres
par colonne , remplir les cases vides de "zéro". ( 0372400)
La virgule vient sur le trait de « droite » de l’unité dm² ß.
|
km2 |
hm2 |
dam2 |
m2 |
dm2 |
cm2 |
mm2 |
||||||||
|
0 |
0 |
0 |
0 |
3 |
7 |
2 |
4 |
0 |
0 ® |
← 0 |
0 |
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
la "grandeur" à
convertir est maintenant placée dans le tableau il ne reste plus qu ' à
effectuer la conversion dans
l'unité demandée.
4 °) faire la conversion :
Déplacer la virgule ; la mettre sur le trait vertical
"droit" de l' unité "demandée " (ici
sur le trait vertical entre dm²
et cm² )
5°) Reporter le résultat : (lu dans le tableau :000
0372400,0000 dm² soit 372400 dm² )
*remarque : dans le tableau
une colonne "unité" contient
deux "sous -colonnes" est
limitée par 2 traits verticaux , l'un à droit l'autre à gauche . La virgule est dite flottante ;elle se trouve toujours sur le trait vertical "limite
droite" de l 'unité concernée.
|
km2 |
|
hm2 |
|
dam2 |
|
m2 |
|
dm2 |
|
cm2 |
|
mm2 |
|
|||||||
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- †Activités :
1°) placer dans le tableau
les aires suivantes :
7 563 m ² ; 74 cm² ; 249 mm² ; 45 ,
4 dm² ;
pour convertir on complète de
"0"
|
km2 |
hm2 |
dam2 |
m2 |
dm2 |
cm2 |
mm2 |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2°) En
utilisant le tableau précédent faire
les conversions demandées :
7 563 m ² ; 74 cm ² ; 249 mm ² ; 45 ,
4 dm ² ;
|
|
|
k m² |
h m² |
dam ² |
m ² |
dm ² |
cm ² |
mm ² |
|
7563 m² |
= |
|
|
|
|
|
|
|
|
74 cm ² |
= |
|
|
|
|
|
|
|
|
249 mm ² |
= |
|
|
|
|
|
|
|
|
45,4 dm ² |
= |
|
|
|
|
|
|
|
|
f ) Mesure agraire : Les multiples
et sous multiples de l’ unité d’aire
m² : |
Travaux : système agraire |
=Définition : on appelle
« mesures agraires » les mesurent qui servent à évaluer la superficie
des propriétés foncières , comme celle des champs ,
des bois , etc.,…
=Les unités de mesures agraires.
1°) L ’
unité principale : l’unité des
mesures agraires est l’ « are » . L’are ( « a »)
est une surface qui égale un
décamètre carré . ( = 100 m²)
2°)
Multiple et sous multiple
« usités » :
L’are n’a qu’un multiple , l’hectare , et un sous multiple le centiare.
L’hectare (
ha) égale 100 ares ( = 10 000 m²) ;
Le centiare ( ca) égale la 100e
partie de l’are ( = 1 m²).
On peut utiliser le
tableau suivant pour effectuer des conversions dans les mesures agraires.
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
ha |
daa |
a |
da |
ca |
ma |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
EN RESUME : on peut superposer les deux tableaux :
La "clef"
qui permet de superposer les deux tableaux , ( les m²
et les mesures agraires ) est
Un are est égal à l’aire d’un carré qui a 10 mètre de côté
. Soit 1 are = 100m ²
|
km2 |
hm2 |
dam2 |
m2 |
dm2 |
cm2 |
mm2 |
||||||||
|
|
|
|
ha |
daa |
a |
da |
ca |
ma |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
CORRIGE :
LES LONGEURS : Corrigé ,
Activité 1
|
km |
hm |
dam |
m |
dm |
cm |
mm |
|
2 |
3 |
4 |
6 |
0 |
0 |
0 |
|
0 |
0 |
1 |
2 |
8 |
7 |
4 |
|
0 |
0 |
0 |
5 |
3 |
4 |
2 |
|
0 |
0 |
0 |
4 |
6 |
5 |
0 |
|
|
|
|
7 |
4 |
|
|
Corrigé
Activité 2
On place les virgules , et les
chiffres ; lorsque les valeurs sont placées dans le tableau il suffit de
déplacer la "virgule" !!!!
|
km |
hm |
dam |
m |
dm |
cm |
mm |
|
2 |
3 |
4 |
6 |
0 |
0 |
0 |
|
0 |
0 |
1 |
2 |
8 |
7 |
4 |
|
0 |
0 |
0 |
5 |
3 |
4 |
2 |
|
0 |
0 |
0 |
4 |
6 |
5 |
0 |
|
0 |
0 |
0 |
7 |
4 |
0 |
0 |
Résultats : 2,346
km =
23 4 6 0 dm =
2346 m ; 12, 874 m = 128 , 74 dm
= 12 874 mm ; 5342 mm
= 5 , 342 m = 53
, 42 dm ; 465 cm = 4650 mm
= 4,65 m ; 74 dm = 0 , 074 hm
= 7400 mm
Corrigé des †Activités :
1°)
placer dans le tableau les aires suivantes :
7
563 m ² ; 74 cm² ;
249 mm² ; 45 , 4 dm² ;
pour convertir on complète de "0"
|
km2 |
hm2 |
dam2 |
m2 |
dm2 |
cm2 |
mm2 |
||||||||
|
0 |
0 |
0 |
0 |
7 |
5 |
6 |
3 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
7 |
4 |
0 |
0 |
|
|
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
2 |
4 |
9 |
|
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
4 |
5 |
4 |
0 |
0 |
0 |
|
2°) En utilisant le tableau
précédent faire les
conversions demandées :
7
563 m ² ; 74 cm ² ;
249 mm ² ; 45 , 4 dm ² ;
|
|
|
k m² |
h m² |
dam ² |
m ² |
dm ² |
cm ² |
mm ² |
|
7563
m² |
= |
0,007563 |
0,7563 |
75,63 |
7563 |
756300 |
75630000 |
|
|
74
cm ² |
= |
0,0000000074 |
0,00000074 |
0,000074 |
0,0074 |
0,74 |
74 |
7400 |
|
249
mm ² |
= |
0,000000000249 |
0,0000000249 |
0,00000249 |
0,000249 |
0,0249 |
2,49 |
249 |
|
45,4
dm ² |
= |
0,000000454 |
0,0000454 |
0,00454 |
0,454 |
45,4 |
4540 |
454000 |
|
Titre |
|
|
N°14 |
TRAVAUX d ’ AUTO - FORMATION sur les
UNITES DE LONGUEUR ; D'ANGLE ; D'AIRE |
1°) Les unités
de longueurs :
a) Quelle
est l'unité principale de longueur ?
b) Construire
le tableau de conversion de longueur.
c) Donner la procédure pour effectuer une conversion avec ce tableau.
2°) Les
angles :
a)
nommer les deux unités d'angles .
b ) donner la procédure permettant le passage d'une écriture sexagésimale
en écriture décimale.
donner la procédure permettant le passage d'une écriture décimale
en écriture sexagésimale :
d)
compléter les phrases suivantes :
La mesure
de l'angle est généralement exprimée ………….. : Un
angle droit mesure ……… .
La
mesure de l'angle est aussi exprimée en grade , alors un angle droit mesure ………grades .
e) Quel est l'égalité des 2 rapports qui permet d 'exprimer des degrés en grades ou des grades en degrés
? :
e )Compléter le tableau suivant
|
Unités |
Symbole |
Equivalence |
Remarque : |
|
Degré |
|
1° = …… ' = ……….." |
Dans
un degré il y a ……. minutes. |
|
Minute
|
|
1
' =
……. ° |
Dans
une minute il y a ……. secondes |
|
Seconde
|
|
1" =
…….' = ……..° |
Dans
une seconde il y a ……… ou …………… de seconde . |
a) Quelle
est l'unité d'aire principale ?
b) Construire
le tableau de conversion de l'aire .
c) Donner la procédure pour effectuer une conversion avec ce tableau
.
TRAVAUX N°
14 d ‘ AUTO - FORMATION :
EVALUATION
1°) faire la conversion
d'unités de longueurs ; compléter le tableau
a) faire
les conversions suivantes :
2,346 km = …………………..
dm = …………………
m
12, 874 m = …………………. dm
= ……………….. mm
5342 mm =
……………………. m =
………………. dm
465 cm =
……………………. mm =
………………. m
74 dm =
……………………… hm
= ……………….. mm
b) faire la conversion d'unités de longueurs ;
compléter le tableau :
|
3,7 km |
= |
………………m |
= |
…………………cm |
|
147 m |
= |
………………dam |
= |
…………………cm |
|
0,73 dm |
= |
……………… cm |
= |
…………………mm |
|
9 cm |
= |
………………m |
= |
…………………mm |
|
65 mm |
= |
………………cm |
= |
…………………m |
c ) faire la
conversion d'unités de longueurs ; compléter le tableau :
|
0,045 km |
= |
………………m |
= |
…………………cm |
|
1,476 m |
= |
………………dam |
= |
…………………cm |
|
43 dm |
= |
……………… cm |
= |
…………………mm |
|
659 cm |
= |
………………m |
= |
…………………mm |
|
6245 mm |
= |
………………cm |
= |
…………………m |
2°) Les angles :
a) Passer
d'une mesure en "degré" en mesure
"grades":
|
Degrés |
Calculs : |
Grades |
|
67° |
|
|
b)
Passer d'une mesure en "grade"
en "degré" :
|
Grades |
Calculs : |
degrés |
|
67 gr |
|
|
c) passage
d'une écriture décimale en écriture sexagésimale :
|
Valeur
décimale |
Valeur
sexagésimale |
|
|
0,1° |
|
|
|
0,5° |
|
|
|
13,5 ° |
|
|
|
29,67 ° |
|
|
d)passage d'une écriture sexagésimale en écriture décimale.
|
Valeur sexagésimale |
On multiplie les minutes par: |
conversion |
|
6' |
|
|
|
13° 30' |
|
|
|
62° 15' |
|
|
|
46° 22' 45" |
|
|
e) Conversion d'unités d'angle , compléter :
|
17,75° |
= …………….° ……………...' |
|
|
49,15° |
= …………….° ……………...' |
|
|
32,50° |
= …………….° ……………...' |
|
|
5,4° |
= …………….° ……………...' |
|
|
73,60° |
= …………….° ……………...' |
|
f) Conversion d'unités d'angle , compléter :
|
35,55° |
= …………….°
……………...'…………." |
|
|
49,23° |
= …………….°
……………...'…………." |
|
|
32,92° |
= …………….°
……………...'…………." |
|
|
5,48° |
= …………….°
……………...'…………." |
|
|
73,65° |
= …………….°
……………...'…………." |
|
g) Conversion en écriture décimale , compléter :
|
35° 15' |
= …………….° ……………… |
|
|
49° 30' |
= …………….° ……………… |
|
|
32 ° 45 ' |
= …………….° ……………... |
|
|
5° 60' |
= …………….° ……………... |
|
h) Conversion en écriture décimale , compléter L arrondir à deux décimales :
|
35° 17' |
= …………….° ……………… |
|
|
49° 31' |
= …………….° ……………… |
|
|
32 ° 36 ' |
= …………….° ……………... |
|
|
5° 2' |
= …………….° ……………... |
|
j) Conversion en grade , compléter L arrondir à deux
décimales
|
35° |
= ………….……………gr |
|
|
24,2° |
= ……………………….gr |
|
|
32,92 ° |
=………… …………….gr |
|
|
5° 2' |
=………… …………….gr |
|
k) Convertir en degrés avec une
écriture décimale arrondir à 0,01 près .
|
1 gr. |
|
|
|
17,5 gr. |
|
|
|
42,75 gr. |
|
|
3°) les conversions d'unités
d'aire .
a) faire
les conversions suivantes :
2,346 km² = …………………..
dm² = …………………
m²
12, 874 m² =
…………………. dm² =
……………….. mm²
5342 mm ² = …………………….
m ² = ……………….
dm²
465 cm² =
……………………. mm ² =
………………. m²
74
dm² = ……………………… hm ²
= ……………….. mm²
b) faire la conversion d'unités d'aire ;
compléter le tableau :
|
3,7 km² |
= |
………………m² |
= |
…………………cm² |
|
147 m² |
= |
………………dam² |
= |
…………………cm² |
|
0,73 dm² |
= |
……………… cm² |
= |
…………………mm² |
|
9 cm² |
= |
………………m² |
= |
…………………mm² |
|
65 mm² |
= |
………………cm² |
= |
…………………m² |
c ) faire la
conversion d'unités d'aire ; compléter
le tableau :
|
0,045 km² |
= |
………………m² |
= |
…………………cm² |
|
1,476 m ² |
= |
………………dam² |
= |
…………………cm² |
|
43 dm ² |
= |
……………… cm² |
= |
…………………mm² |
|
659 cm² |
= |
………………m² |
= |
…………………mm² |
|
6245 mm² |
= |
………………cm² |
= |
…………………m² |