Pré requis:

Le système sexagésimal
Mesure du temps.
Les angles
Les outils de mesure d’un angle
Les unités d’angle

ENVIRONNEMENT du dossier:

Index warmaths		Objectif précédent : 1°) Addition et soustraction d’heures .	Objectif suivant Les opérations avec les angles .	Liste des cours en géométrie

	DOSSIER : Les nombres complexes
	1°) Définition du nombres « complexe »
	2°) « la CONVERSION » : « ANGLES en degrés » et ou « HEURES » en secondes ; puis en « heure ; minute ;seconde »
	3°) « CALCULS » avec deux nombres : Addition ; soustraction ;multiplication et division.

TEST

COURS

Devoir Contrôle

Devoir évaluation

Interdisciplinarité

Corrigé Contrôle

Corrigé évaluation

COURS

1°) Définition du nombres « complexe »

nous connaissons le nombre dit « entier » , ensuite nous avons appris à reconnaître le nombre dit « décimale » ; dans cette leçons nous allons rencontrer un nouveau nombre dit « nombre complexe ».

le nombre complexe est un nombre qui est utilisé pour exprimer :

- la valeur d’un angle en « degré minute ;seconde. »

- ou la valeur du temps en « heure ; minute seconde » ;

Exemples :

- en géométrie : un angle ( en degré) mesure : 47 degrés 24 minutes et 35 secondes ( ce qui donne l’écriture du nombre dit « complexe » : 47 ° 24 ‘ 35’’ )

- pour désigner la mesure du temps qui passe : 3 heures 18 minutes 15 secondes (donnera l’écriture : 3 h 18’ 15’’ ; ce nombre appelé nombre complexe )

Le système de numération utiliser est appelé : « Le système sexagésimal» ( calcul en base « 60 »)

Rappels :

Un degré = 60 minutes = 3600 secondes ;

Une heure = 60 minutes = 3600 secondes ;

Et dans tous les cas : une minute = 60 secondes

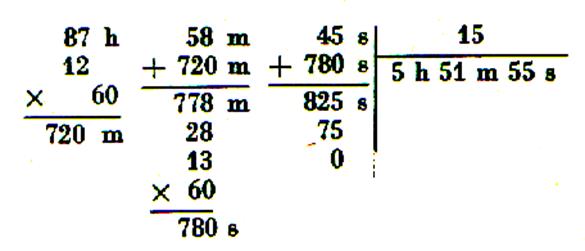
1°) Conversion en secondes :

- exemple 1 :

soit un angle mesure 5° 35’ 28’’

Conversion des degrés en secondes	5° = 3600’’ 5 = 18 000’’
Conversion des minutes en secondes	35’ = 60’’ 35 = 2100’’
Nombres de secondes « seules »	28’’
Total : 5° 35’ 28’’ = 20 128’’

Conclusion : un angle mesure : 5° 35’ 28’’ mesure 20 128’’ ( secondes)

- exemple 2 :

soit la durée d’un parcours est de 5 h 35’ 28’’

Conversion des heures en secondes	5 h = 3600’’ 5 = 18 000’’
Conversion des minutes en secondes	35’ = 60’’ 35 = 2100’’
Nombres de secondes « seules »	28’’
Total : 5° 35’ 28’’ = 20 128’’

Conclusion : la durée du parcours est de : 5 h 35’ 28’’ ou de 20 128’’ ( secondes)

- exemple 2 :

soit la durée d’un parcours est de 5 h 35’ 28’’

Conversion des heures en secondes	5 h = 3600’’ 5 = 18 000’’
Conversion des minutes en secondes	35’ = 60’’ 35 = 2100’’
Nombres de secondes « seules »	28’’
Total : 5° 35’ 28’’ = 20 128’’

Conclusion : la durée du parcours est de : 5 h 35’ 28’’ ou de 20 128’’ ( secondes)

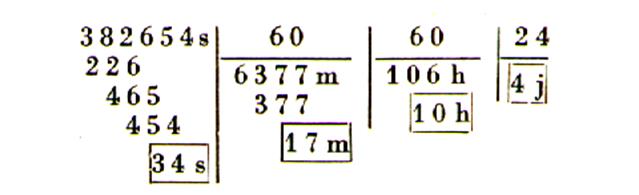
2°) Combien y a –t- il de degrés , minutes , secondes dans 45 872 ’’ ?

	Pré requis : la division euclidienne
Nombres de degrés	45 872 : 3600 = 12° et il reste 2672’’
Nombres de minutes	2672’’ : 6O = 44’ et il reste 32’’
Résultat : 45 872 ’’ = 12° 44’ 32’’

2°) Les opérations dans le système sexagésimal.

Exemples des 4 opérations . ( applicables aux : « heure, minute seconde » et « degré, minute ,seconde »	Résultat
( 32° 17’ 27’’ ) x 3	96° 51' 81'' : 96° 52' 21''
( 27° 17’ 20’’) : 3	61° 51' 60'' = 61° 52' 00''
42° 13’ 20’’ - 27° 12’’	15° 1' 20''
42° 13’ 10’’ + 25° 57’ 27 ‘’	67° 70' 37'' = 68° 10' 37''

ADDITION

Voir :explication graphique

Exemple : calculer la somme des angles A = 12° 52’ et B = 8°26’

Nous disposons l’opération comme s’il s’agissait de nombres entiers , puis nous additionnons séparément les unités de même nom ( minutes avec minutes ; degrés avec degrés) nous obtenons : 20° 78’

Or : 78’ = 1° 18’

Nous écrivons donc 18’ dans la colonne des minutes et nous reportons 1° dans celle des degrés .

D’où le résultat : + = 21° 18’

12° 52’

8°26’

20° 78’

1° 18’

21° 18’

B) Additionner deux expressions sexagésimales : 42° 13’ 10’’ + 25° 57’ 27

42° 13’ 10’’ + 25° 57’ 27 Procédure:
1) Additionner chaque groupe : Degré Minutes secondes	42+25 13+57 10+27	67° 70' 37''
2)convertir les secondes en minutes	37'' = 0' 37''
3) convertir les minutes en degré	70' = 1° 10'
4) rajouter les degré aux degrés ; les minutes aux minutes ;….	67° +1° 10'+ 0' 37'' = 68° 10' 37''
5) rendre compte	42° 13’ 10’’ + 25° 57’ 27 = 68° 10' 37''

Multiplication:

Voir :explication graphique

L’angle A mesure 17° 28’37’’ ; calculer la mesure de l’angle B tel que : = 3

Nous avons = 17° 28’37’’ 3

Nous disposons l’opération comme s’il s’agissait de nombres entiers , puis nous multiplions séparément par le multiplicateur « 3 » les unités de même nom.

Nous obtenons 51° 84’ 111’’ , soit , par conversions successives 51° 85’51’’ ;

Puis 52° 25’ 51’’

D’où le résultat = 3 = 52° 25’ 51’’

17° 28’37’’

51° 84’ 111’’

1’ 51’’

85’

1° 25’

52° 25’ 51’’

Multiplier une expression sexagésimale par un nombre: 3 ( 32° 17’ 27’’ )

3 ( 32° 17’ 27’’ ) Procédure:
1) Multiplier chaque groupe :par "3" Degré Minutes secondes	32 fois 3 = 17 fois 3 = 27 fois 3 =	96° 51' 81''
2)convertir les secondes en minutes	81'' = 1' 21''
3) convertir les minutes en degré	……..51'+1'21''
4) rajouter les degré aux degrés ; les minutes aux minutes ;….	51' 81'' = 52' 21''
5) rendre compte

Division.

Voir :explication graphique

Exemple : on partage en 5 parties égales un angle A qui mesure 45°16’35’’. Calcul de la mesure de chacun des angles obtenus .

Nous pouvons effectuer l’opération 45°16’35’’ : 5

Disposons cette opération comme s’il s’agissait de nombres entiers , puis divisons séparément par le diviseur 5 les unités de même nom:

45° : 5 = 9°

16’ : 5 = 3’ ; il reste 1’ que nous transformons en secondes , soit 60’ , qui sont ajoutées à 35’ font 95’ .

95’ :5 = 19’’

d’on le résultat : = 9° 3’ 19’’

45°16’35’’ : 5

0 1’ 9° 3’ 19’’

60’’

95’’

45’’

0’’

Diviser une expression sexagésimale par un nombre: ( 33° 21’ 27’’ ) : 3

( 33° 21’ 27’’ ) : 3 Procédure:
1) diviser chaque groupe :par "3" Degré Minutes secondes	33 : 3 = 21: 3 = 27 : 3 =	11° 7' 9''
2)convertir les secondes en minutes éventuellement.
3) convertir les minutes en degré : éventuellement.
4) rajouter les degré aux degrés ; les minutes aux minutes ;…. éventuellement.
5) rendre compte	( 33° 21’ 27’’ ) : 3 = 11° 7' 9''

Soustraction:

Voir :explication graphique

Calculer la différence des angles = 37° 46’ 25’’ = 17°54’15’’

Nous avons :

- = 37° 46’ 25’’- 17°54’15’’

37° 46’ 25’’ = 17°54’15’’

nous disposons l’opération comme s’il s’agissait de nombres entiers , puis nous essayons de soustraire les unités de même nom

Nous pouvons soustraire 15’’ à 25’’ , mais nous ne pouvons soustraire 54’de 46’.Nous prélevons au nombre supérieur(degré) 1° que nous transformons en 60’.

Le nombre 37° 46’ 25’’ devient 36° 106’ 25’’ .

Nous avons

36° 106’ 25’’- 17° 54’ 15’’= 19° 52’ 10’’

d’où le résultat : - = 19° 52’ 10’’

37° 46’ 25’’

- 17° 54’15’’

------------ ------

Soustraction impossible

36° 106’ 25’’

- 17° 54’ 15’’

------------ ------

19° 52’ 10’’

Autres exercices résolus

sexa1

sexa2

sexa3

sexa4

sexa5

sexa6

TRAVAUX AUTO FORMATIFS.

CONTROLE :

1. recherche dans le dictionnaire : définition de système décimal ?

EVALUATION

CONVERSIONS :

1°) Conversion en secondes :

5° 35’ 28’’

2°) Combien y a –t- il de degrés , minutes , secondes dans 45 872 ’’ ?

Faire les calculs suivants ( poser les opérations ) :

1°)Calculer la somme des angles A = 12° 52’ et B = 8°26’

2°)L’angle A mesure 17° 28’37’’ ; calculer la mesure de l’angle B tel que :

= 3

3°)On partage en 5 parties égales un angle A qui mesure 45°16’35’’. Calcul de la mesure de chacun des angles obtenus .

4°) Calculer la différence des angles = 37° 46’ 25’’ = 17°54’15’’

A l’aide de la calculatrice ,passer d’un système à l’autre :

Calculer et mettre le résultat sous forme sexagésimale :

Série 1
42° 13’ 20’’ - 27° 12’’ =
42° 13’ 10’’ - 25° 57’ 27 ‘’ =
( 33° 21’ 27’’ ) : 3 =
42° 13’ 10’’ + 25° 57’ 27=
3 ( 32° 17’ 27’’ ) =

Calculer et mettre le résultat sous forme sexagésimale.

Série 2	Réponses
35°11’29’’+17°50’38’’=
17,35h – 5h 43min 17 sec =
11h 5min 22 sec – 3 h 38 min =
3,475h 2,8 =
17° 37’ 45’’ 5,3 =
12h44min : 8 =
36°19’56’’0,75 – 25,475° =

Les unités d’angle

COURS

Et dans tous les cas : une minute = 60 secondes

Série 2

Réponses