Pré requis:

Angles : conversions

Notion d’angle

ANGLES : terminologie

ENVIRONNEMENT du dossier:

Index : accueil warmaths

Objectif précédent

Objectif suivant

tableau >> vers la liste de cours

DOSSIER:

« les ANGLES » OPERATIONS : (calculs graphiques)

TEST :

COURS :

Devoir Contrôle

Devoir évaluation

Interdisciplinarité :

Corrigé Contrôle

Corrigé évaluation

COURS

RAPPELS : « Angles adjacents » :

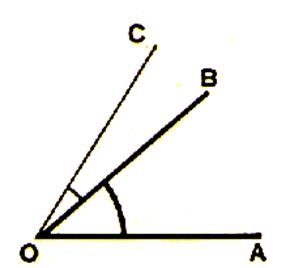
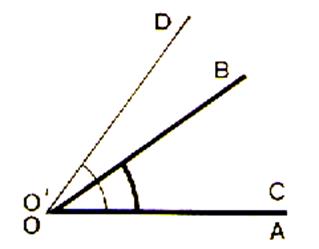
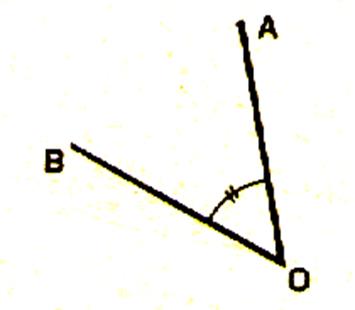
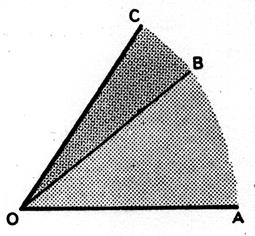
Angles adjacents : Les angles COB et BOA sont dits « adjacents »
Deux angles adjacents sont deux angles qui : -Ont un sommet commun -On un coté commun -Sont situés de part et d’autre du coté commun.

COMPARAISON de DEUX ANGLES

Pré requis : les relations d’ordre

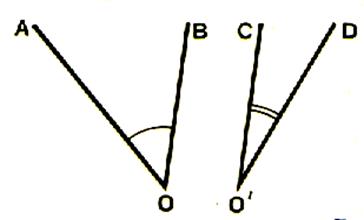
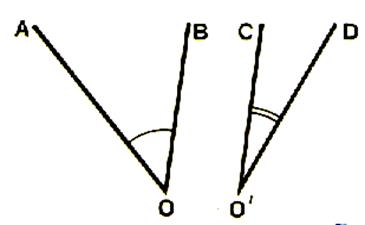
Activité : Considérons deux angles AOB et CO’D . A l’aide d’un papier transparent , calquons l’angle CO’D , puis faisons glisser le calque de manière que les côtés O’C et OA soient superposés et que les deux angles aient une partie commune .

Trois cas peuvent se présenter :

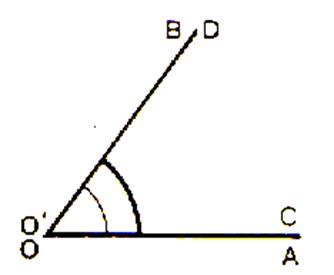
Premier cas :	Les côtés O’D et OB sont confondus
Les deux angles coïncident ; nous dirons qu’ils sont égaux . Nous écrivons : =

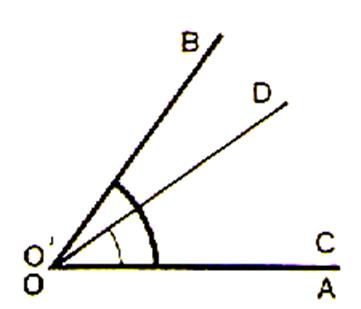
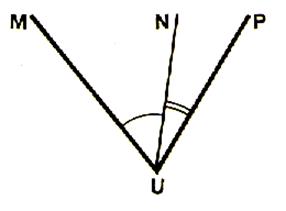
Deuxième cas :	Le côté O’D de l’angle CO’D se place entre OA et OB.
L’angle CO’D est plus petit que l’angle AOB . Nous écrivons : <

Troisième cas :	Le côté O’D de l’angle COD se place au – delà de OB
L’angle CO’D est plus grand que l’angle AOB. Nous écrivons : >

Remarque : si nous comparons successivement un angle plat à un angle saillant puis à un angle rentrant , nous constatons qu’un angle saillant est inférieur à un angle plat , et qu’un angle rentrant est supérieur à un angle plat .

OPERATIONS :

Somme de deux angles	INFO PLUS : Calculs
Considérons deux angles AOB et CO’D
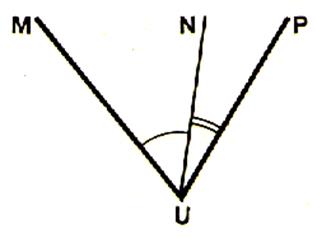
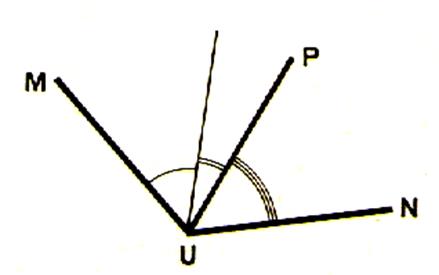
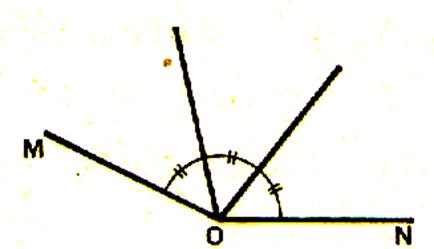
Construisons un angle MUN égal à l’angle AOB , puis un angle NUP égal à l’angle CO’D , de manière que les angles MUN et NUP soient adjacents

L’angle MUP est la somme des angles AOB et CO’D.

L’opération que nous venons d’effectuer est l’addition des angles AOB et CO’D.

Nous pouvons écrire : = +

Nous admettons que l’ addition de deux angles est une opération commutative ; c’est à dire que si nous formons la somme + , nous obtenons un angle égal à .

Nous écrivons : = + = +

Somme de plusieurs angles :
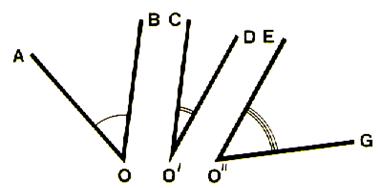
Considérons trois angles AOB , CO’D ,EO’’G .
Nous construisons successivement l’angle MUP somme des angles AOB et CO’D , puis l’angle MUN somme des angles MUP et EO’G.

L’angle MUN est la somme des angles AOB , CO’D , EO’’G additionnés dans cet ordre .

Nous écrivons :

= + + = ( + )+

Nous admettrons que l’addition des angles est une opération associative , c’est à dire que nous avons l’égalité :

( + )+ = + (+)

de la même manière , nous réaliserons la somme d’un nombre quelconque d’angles .

Niveau plus

Cas où la somme des angles est supérieur à un angle plein

DIFFERENCE DE DEUX ANGLES	INFO PLUS : Calculs
Construisons l’angle MUP , somme des deux angles AOB et CO’D
Par définition , l’angle CO’D est la différence des angles MUP et AOB.

Nous pouvons écrire : = + Û= -

MULTIPLE d’un ANGLE :	INFO PLUS : Calculs
Soit l’angle AOB
Construisons l’angle MON somme de trois angles

L’angle MON contient trois fois l’angle AOB ; nous écrirons :

= 3

Nous disons que l’angle MON est un multiple de l’angle AOB

DIVISION voir inverse de la multiplication
Partages d’un angle en parts égales	INFO PLUS : Calculs

TRAVAUX AUTO FORMATIFS.

CONTROLE :

Aucun

EVALUATION :

24°) Trouver deux angles supplémentaires dont l'un soit le quadruple de l'autre.

25°) Trouver deux angles complémentaires dont l'un soit le double de l'autre.

26°) mesurer les angles ; les nommer. Etablir une égalité.