Pré requis:

Le cercle : sa symbolique

ENVIRONNEMENT du dossier:

Index

Objectif précédent : 1°)Le degré (initiation à la mesure) 2°)La durée

Objectif suivant: Les unités d'angles

tableau

INFO : LE DEGRE (son origine ?) ; une explication ! ! ! !

Pourquoi avoir découpé un cercle en 360 parties égales ?

Ou l' origine du mot "degré" dans la mesure d’un angle .

A) Pour tracer le premier calendrier circulaire

1°) On observe qu’il existe 4 saisons :

Chaque saison dont le début ou la fin correspond à des phénomènes observables (solstice ou équinoxe )

2°) On observe que pendant chaque saison s ‘est effectué 3 cycles de lunes ,

3 ° ) On observe que pendant chaque cycle de lune il y a environ 30 alternances de jours et de nuits .

Il faut mettre en relation le cercle , les 4 saisons , le nombre de cycles de lunes , le nombre d’alternances de jour et de nuits en un cycle de lune .

Ainsi le nombre de jours dans chaque saison comptait-il environ 90 jours .

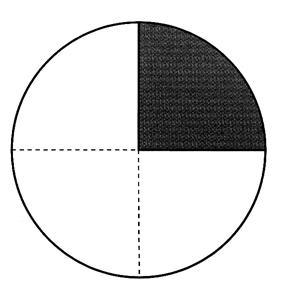
Pour obtenir ce calendrier , on trace un cercle :

On trace une droite passant par le centre du disque.

On trace une droite perpendiculaire passant par le centre du cercle .

Le cercle ou disque est découpé en 4 parties égales .

Remarques : les moyens de mesurer le temps étant de plus en plus précis ,nous sommes parvenus à compter 365 jours ¼ par année civile. Nous sommes obligés d’avoir une année bissextile (tous les quatre ans nous rajoutons un jour à l’an , pour compenser la perte du ¼ de jour à compter chaque année ) .

Pour représenter ces observations on est parti de la forme la plus parfaite et porteur de signification : le cercle , pour représenter graphiquement le cycle d’une année .

OBSERVATIONS :	TRACE
	On prend le cercle comme forme géométrique (forme du soleil , ou forme de la lune dans sa phase « pleine lune)pour établir un calendrier « graphique »
4 saisons revenants régulièrement : (printemps, été, automne , hiver)	On divise le cercle en quatre parties égales.
Pour chaque changement de saison on observe : Les marées ; le solstice d’été (vers le 21 juin : le jour le plus long donc la nuit la plus courte )et le solstice d’hiver (le jours le plus court et la nuit la plus longue : le 21 décembre), L’ équinoxe de printemps (20 mars) et l’équinoxe d’automne (21 mars) (équinoxe : chacune des deux époques de l’année où le jour est égal à la nuit pour toute la terre , le grand cercle de la sphère de la terre limitant la partie éclairée , passe par le pôle)
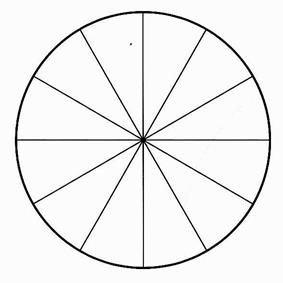
Pendant ces 4 saisons on observe 3 cycles de lunes	On divise les quarts de cercle en trois parties égales
Pour chaque cycle de lune on observe qu’il y a environ 30 alternance de nuits et de jours	On découpe ces tiers précédents en trente parties égales.
Nous avons ainsi découpé le cercle en 360 parties égales. C’est ainsi que fut obtenu le premier calendrier.	Chaque partie : fut appelée « degré » Le cercle compté 360 degrés
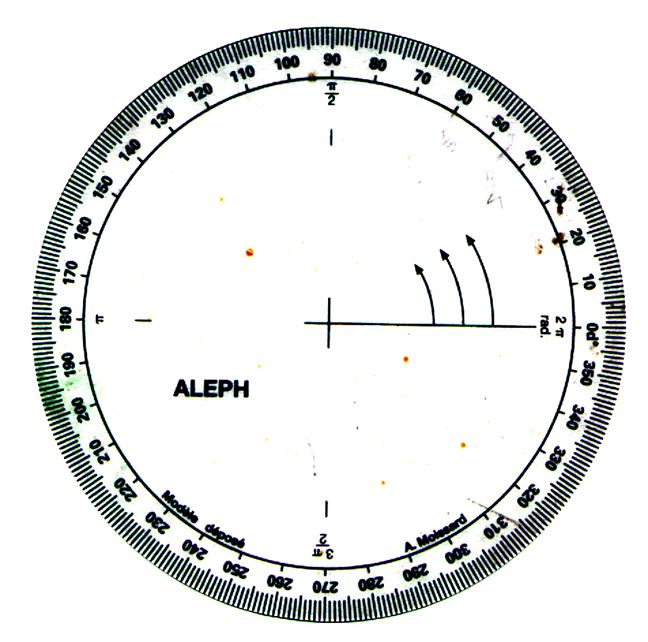
Ceci est un degré !!
REMARQUE :La science ayant progresser : les moyens de calculs , font qu’aujourd’hui une année compte 365 jours et ¼ ;l’année bissextile « rattrape » ces « 4/4 de jours » tous les quatre ans. Ainsi tous les quatre ans , une année compte 366 jours , cette journée étant rajoutée au mois de février.

CERCLE :