Fiche 1 : Volume du parallélépipède rectangle

Fiche 2 : Volume du prisme droit

Fiche 3 Calcul du volume des prismes vus dans la leçon : les prismes droits et perspectives  fiche 4

Fiche 4 : Modèles de rédaction de problèmes élémentaires

Fiche 5 : Exercices

Fiche 6 : Problèmes sur le prisme.  ( en plus , pas obligatoire )

Fiche 7  Volume du cylindre de révolution.

Fiche 8 : Situations problèmes sur le cylindre…….

Fiche 9 Représentation graphique.  (niveau + facultatif)

Fiches de travail

Fiche 1 :volume du parallélépipède rectangle.

SOS rappel

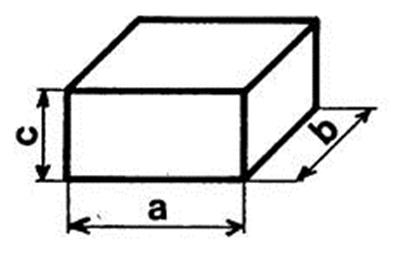
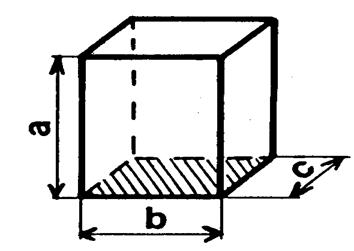
Vous avez vu au niveau précédent ( 6^ème ) que une unité de longueur étant choisie  « a » , « b »  et « c » , étant les dimensions du parallélépipède rectangle, son volume « V » (avec l’unité correspondante) est :   «  »

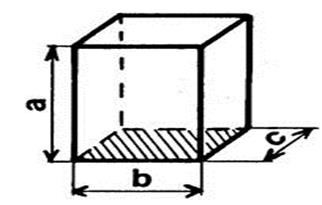
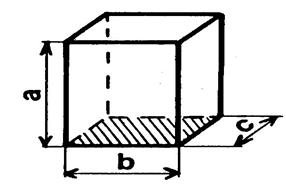
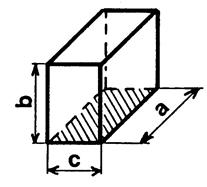
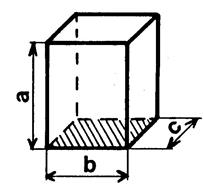
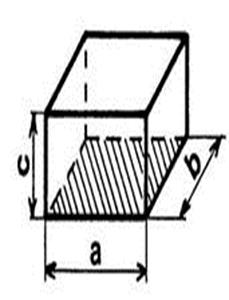
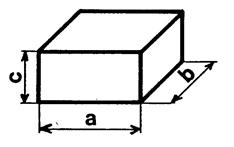
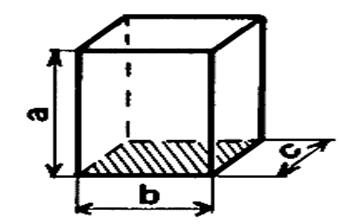
On peut considérer la parallélépipède rectangle comme un prisme.

IL y a « 3 » façons de choisir la base.

Appelons « A » l’aire de la base et « h » la hauteur correspondante.

 ;  

 ;  

 ;  

  = 

  = 

  = 

Dans tous les cas , le volume est égal au produit de l’aire  de la base par la hauteur correspondante.

Activité n°  1  ….

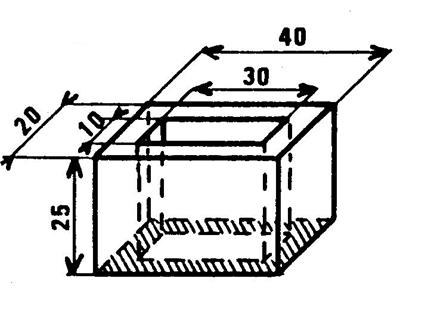
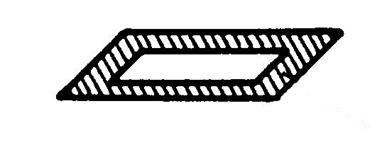
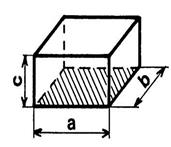
Ci-contre on vous donne une brique creuse .

Elle est constituée par un parallélépipède rectangle traversé transpercé par un parallélépipède rectangle creux.

On vous demande de calculer le volume de matière que constitue cette brique.

Les dimensions de la figure sont en « cm ».

On vous propose 2 méthodes  pour trouver  le résultat.

1^ère méthode : 

a)     Volume du grand parallélépipède.

Volume de la brique (quantité de matière) :

Soit

2^ème méthode.

On recherche la surface de base de la brique.

Appelons  la surface de base du grand parallélépipède.

Appelons  ;la surface de base du petit parallélépipède rectangle

Appelons « B » la soustraction des surfaces de bases. ( ci-dessous la surface hachurée)

 =   30

B =  800 – 300 = 500  

Son volume est de

Son volume est de :

En mettant « h » en facteur on obtient l’égalité :

La brique peut être considérée comme un prisme droit de hauteur « h » et dont l’aire    

Le volume est alors le produit de l’aire de la base par la hauteur :

Puisque l’aire de la base est  « 

Le volume de la brique en  est de     soit :        

Activité n°  2  ….

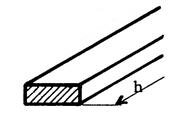
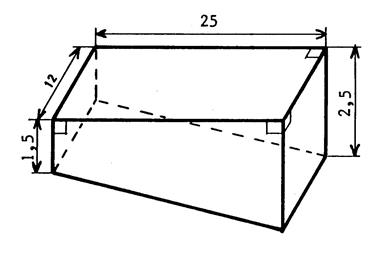
Ci-dessous on vous donne en perspective cavalière d’une portion de poutrelle métallique de « 7 m » de long.

Les dimensions du dessin sont en « cm ».

Ci-dessous on vous donne en perspective cavalière la vue explosée de la poutre , se ramenant  à l’assemblage de 3 parallélépipède rectangle de « 7 m » de long .

On vous demande de calculer le volume de cette poutrelle.

On peut considérer que cette poutrelle est un prisme droit dont la base est un prisme droit dont la base à la forme d’un « T ».

On peut la décomposer en « 3 »  parallélépipèdes rectangles.

Pour calculer le volume de la poutrelle, on peut calculer le volume de chacun des parallélépipèdes rectangles  puis en faire la somme.

Mais  on peut aller plus vite en utilisant la méthode n°2 : addition des « 3 »  surfaces élémentaires de base.  ( ) .

Les trois parallélépipèdes rectangles ont la même longueur.

V₁  = 

V₂

V₃

Le volume de la poutrelle est alors :    .

On peut mettre en facteurs, ce que nous écrivons :   .

Or  ( ) .n’est autre que l’aire de la base de la poutrelle. Appelons -la «  B ».

Le volume « V » est alors le produit de l’aire de la base « B » par la hauteur « h ».

Calculez le volume en utilisant cette formule :

Aire de la base en « cm² » :

Volume en  « cm³ »  .   ; le volume de la poutrelle est de  « 301 000 cm³ »

Fiche 2 : Volume du prisme droit. ( voir la fiche 1 , leçon …sur le prisme droit et  construction  ……..)

Prenez le prisme à base triangulaire que vous avez construit ; de la leçon signalée ci-dessus.

Vous allez en déterminer le volume en « cm³ »en cherchant combien de cube de 1 cm de côté il peut contenir.

( le quadrillage est constitué par des carrés de ½  cm de côté.)

Commencez par compter combien il faut de cubes pour recouvrir exactement la base triangulaire ( ces cubes étant entiers ou découpés en morceaux).

Pour cela vous pouvez considérer le triangle comme étant la moitié d’un rectangle ( voir la figure ci-contre).

Nombre de cubes nécessaires : ….( 6 fois 7) /2  = 42 /2 = 21.

Ce nombre  n’est autre que la mesure en « cm² »  de l’aire de la base triangulaire du prisme. Soit …..21 cm²………

Nombre total de cubes :   …… ………= …………. Le volume du prisme est donc ………..cm³ ….

En  définitive, pour calculer le volume on a multiplié l’aire de base par la hauteur  .

On obtiendrait le même résultat avec n’importe quel  prisme droit. ( que la base soit triangulaire ou non , comme dans la fiche 1 ) On écrira  alors :

A retenir :

Le volume « V » du prisme droit de hauteur « h » et dont l’aire de la base est « B »

Remarque 1 : « V » , « B »  et « h » sont exprimés avec des unités correspondantes.

-         Ce qui signifie que si l’unité de « h » est  le « m » , l’unité de « B » sera le « m ² » et l’unité de « V » sera le « m ³ ».

-        Ce qui signifie que si l’unité de « h » est  le «mm » , l’unité de « B » sera le «mm ² » et l’unité de « V » sera le « mm ³ »…et ainsi de suite.

Remarque 2 : La démarche précédente a été fait avec des nombres entiers .

Dans le cas de nombres à virgule, il suffit d’imaginer un changement d’unité donnant des nombres entiers et on se retrouve dans la même situation.

Fiche 3 Calcul du volume des prismes vus dans la leçon : les prismes droits et perspectives  fiche 4

Reprenons le dessin de la leçon    « les prismes droits et perspectives  fiche 4 »

Nous appelons  « P₁ » ; « P₂ »  et « P₃ » .les « 3 »  prismes  et « V₁ » , « V₂ »  et « V₃ » leurs volumes respectifs.

Les dimensions sur le dessin ,ci-dessous , sont exprimées en « mm » .

Prisme « P₁ » :

Aire de base en « mm² » :……(30 x 10 ) /2 = 300 / 2 = 150 ………..

Volume de Prisme « P₁ » en « mm³ » :…150 x 40 = 6 000…………………

Prisme « P₂ » :

Aire (trapèze) de base en « mm² » :…( 15 + 45 ) 30 /2 =  900……………..

Volume de Prisme « P₂ » en « mm³ » :……900 x 40 = 36 000…………

Prisme « P₃ » :

Aire de base en « mm² » :…( 20 x 30 ) :2  = 600 : 2 = 300……………..

Volume de Prisme « P₃ » en « mm³ » :……300 x 40 = 12 000…………………

Vérification :

Volume du parallélépipède rectangle : 45 x 40 x 30  =  54 000  mm²

Somme  des volumes des prismes en mm² :  6 000 + 36 000 + 12 000  = 54 000 mm²

Conclusion : la vérification satisfait …

Fiche 4 : Modèles de rédaction de problèmes élémentaires.

Exercice -Situation n°1 :

Un prisme a pour volume « 91 cm³ ». L’aire de sa base est « 13 cm² ». Quelle est sa hauteur  ( h ) ?

Résolution :

Formule à utiliser : «  »  . Par transformation de l’égalité ,on en déduit  que  «   »

Hauteur du prisme en « cm ».   «   » ; h  =   7   ; Conclusion la hauteur du prisme est de …7….cm

Exercice - Situation n°2 :

Une barre de fer a la forme d’un prisme à base carrée. Son volume est de « 8 dm³ ».

Sa hauteur est de « 5 m » . Quelle est en « cm » , la longueur du côté de sa base carrée ?.

Résolution :

Formule à utiliser : «  »  . Par transformation de l’égalité ,on en déduit  que  «   »

Conversions :   V = « 8 dm³ »=  8 000 cm³ . ; «  h = 5 m = 500 cm. »

Aire de la base carrée du prisme en cm² .   B = 8000 / 500 = 16 cm².

La longueur du côté en « cm »  est égale à ………

Fiche 5 : Exercices

Exercice 1 : Complétez le tableau relatif à des prismes : ( attention aux unités)

Aire de la base

Hauteur

Volume.

0,46 cm²

0,11 dm

…….mm³

1,2 dm²

……………mm

60 cm³

………….m²

0,84 cm

2,1 d m³

Exercice 2 :

Un prisme a pour base un losange. Sa hauteur est « 4 m » et son volume « 36 m³ ».

Calculez la longueur de ses diagonales sachant que l’une est le double de l’autre.

Fiche 6 : Situations- problèmes sur le prisme.  ( en plus , mais pas obligatoire )

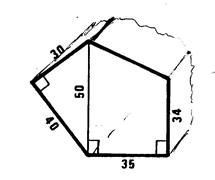
Pb 1

Calculez le volume du prisme. (que vous avez construit en carton .

La base de ce prisme est représentée ci-contre.

Les dimensions sont en « mm ».

La hauteur de ce prisme est de « 65 mm ».

Calculez l’aire du rectangle : ( 40 x 30 / 2 ) , calculez l’aire du trapèze  ( ( ( 50 + 34 ) x 35 ) / 2 = ….

Additionnez les aires . Volume : aire totale par « h »…..

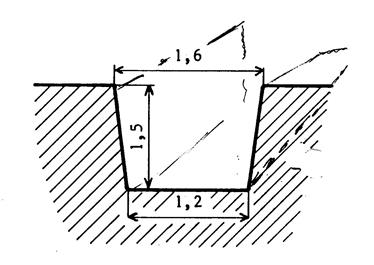
Pb 2 :

On veut creuser une tranchée de « 25 m » de long dont la section est représentée ci-contre.

Les dimensions sont en « m ».

Sachant que , quand la terre est remuée, son volume augmente de « 30 % » .

Combien devra-t-on faire de voyages avec un camion de « 6 m³ »pour enlever cette terre ?

·       Calcul du volume :  Calculez l’aire du trapèze :  ( 1,6 + 1,2 ) x 1,5  , le résultat divisé par 2 .Le résultat fois « 25 »= V.

·       Calculez : V fois 20 / 100 = volume de terre remuée ( V r)  ; faire la somme «  V + Vr = Volume de la terre aprés travaux.( V t)

·       Nombre de voyages : V t / 6 =   prendre la valeur par excès à l’unité prés ..

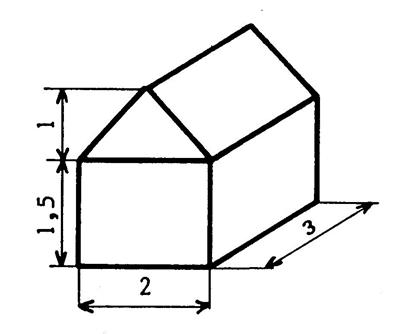
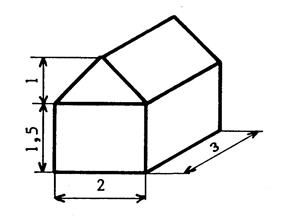
Le dessin ci-contre représente une petite maison.

Les dimensions sont en « m ». Calculez son volume.

1°) Aire totale :   « aire du triangle »  ( 2 fois 1  divisé par 2 )  plus « aire du rectangle »  ( 2 fois 1,5 ) . 2° )  Volume =   aire totale fois  la somme multipliée par « 3 ».

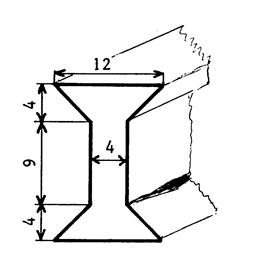
Le dessin ci-contre représente la section d’une poutrelle en fer. De 6 m de long.

Les dimensions sont en « cm ».

Calculez la masse de cette poutrelle sachant que la masse volumique du fer est de « 8,6 kg/ dm³ »

Faire le calcul de l’ aire du trapèze ( ( 12 + 4 ) fois 4 ) / 2 ;   Aire du rectangle :9 fois 4 ;  faire la somme des aires (convertir en dm² ) ; Calcul du volume de la poutrelle : multipliez la somme des aires  par 60 dm .

Pour calculer la masse : multiplier le volume par 8,6 ; la masse est exprimée  en kg. 

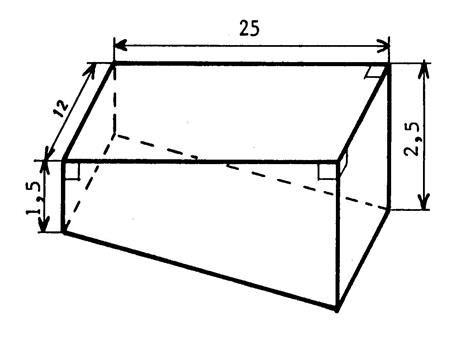
Pb 5 :

Le dessin ci-contre représente une piscine. Les dimensions sont en « m ».

1°)Calculez son volume.

2°) On remplit cette piscine de telle sorte que l’eau arrive à 15 cm du bord . Calculez la quantité d’eau ( en litres )

Ce remplissage a été effectué à l’aide d’un robinet dont le débit et de 12 Litres par seconde.

Combien de temps a-t-il fallu pour remplir cette piscine à la hauteur désignée ? ( en « h » et « mn »)

Faites la rédaction de ce travail sur feuille libre.

Calcul du volume « V1 » du prisme : 1,5 fois 12 fois 25 = …………;

Calcul du volume « V2 »  du prisme à base triangulaire : ( 1 fois 25 / 2 )  12 = ……………...

Faire la somme : V1 + V2 = Vt   ;

Volume d’eau  « Ve »  :   Vt -  ( 0,15 fois 12 fois 25 ) = ………

Multipliez par 1000 pour avoir le volume en litres d’eau .

Divisez le volume d’eau par 12 = …………………….des secondes . 

Divisez par 3600 pour obtenir des heures ; ….

Fiche 7  Volume du cylindre de révolution

Sos Cours sur le volume du cylindre.

Le cylindre de révolution peut être considéré comme un prisme droit particulier dans lequel la base est un disque.

Il suffit d’imaginer que par approximation ce disque est un polygone régulier ayant une infinité de côtés.

Vous concevez alors que la formule donnant le volume du cylindre de révolution soit le même que celle du prisme droit..

A retenir :

Le volume « V » du prisme droit de hauteur « h » et dont l’aire de la base est « B »

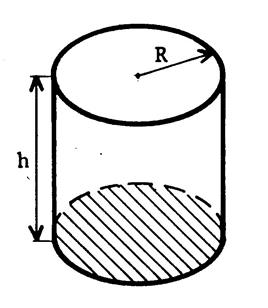
Appelons « R » le rayon du disque de base.

Vous savez que l’aire du disque est égale à «  »

A retenir :

Le volume « V » du cylindre de révolution de hauteur « h » et de rayon « R »

Remarque : « V » , « B » , « h » , « R » sont exprimés avec des unités correspondantes.

Remarque 1 : « V » , « B » , « R »,  et « h » sont exprimés avec des unités correspondantes.

-         Ce qui signifie que si l’unité de « h » est  le « m » , « R » doit être en « m » , l’unité de « B » sera le « m ² » et l’unité de « V » sera le « m ³ ».

Ce qui signifie que si l’unité de « h » est  le «mm » , « R » doit être exprimé en « mm » , l’unité de « B » sera le «mm ² » et l’unité de « V » sera le « mm ³ »…et ainsi de suite.

Activité N°….. Complétez le tableau relatifs à des cylindres ( prendre  = 3,14 )

Rayon

Aire de la base

Hauteur

Volume

5 cm

……78,5…cm²

0,6 m =60 cm

…4710…..cm³

……2…mm

……12,56….mm²

3,5 cm = 35 mm

439,6 mm³

0,7 dm

……153,86….cm²

0,5 cm = 5….mm

76,93  cm³

Activité N° …..

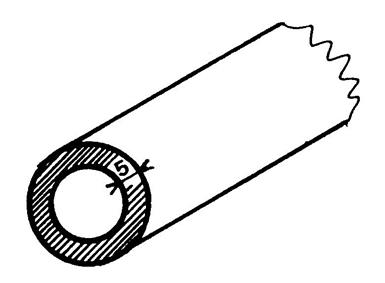
Ci –contre , un tuyau de plomb à « 4 cm » de diamètre extérieur.

Il a une épaisseur de « 5 mm » et une longueur de 3 m.

Calculez son volume et sa masse sachant que la masse volumique du plomb est de «  11,3 g / cm³ ».

Le volume « V » se calcule grâce à la formule «  V =  B x h »

·       La base est une couronne de rayon extérieur : R =  40 mm / 2 =   20 mm   et le rayon intérieur « r » :  « 20 – 5 = 15 mm ».

·       Aire de la base  ( en mm²) :

                  B = ( 3,14 x 20 x 20  ) -  ( 3,14 x 15 x 15 )     ;   B = 1256 -  706,5 ;  B = 549,5 mm²

·       Volume du tuyau (mm³ ) : ( V)

                         V = 549,5 x 3 000 = 1 648 500   mm³    ; V = 1648,500 cm³ 

·       Masse du tuyau en « g ».

                           1 648,  500       x  11,3 =  18628,05     ;   masse du tuyau  =  18,62805 kg

Activité N°…..

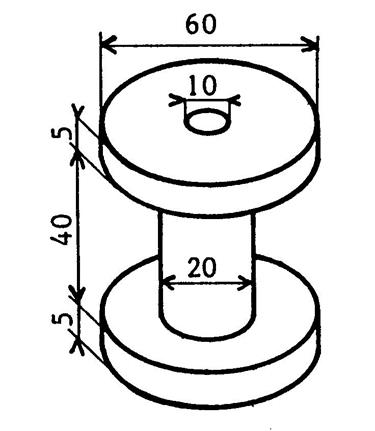
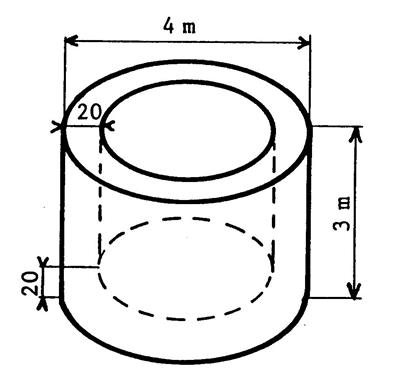
Le dessin ci-contre représente une bobine (de cable électrique ).

Elle est constituée par « 3 » cylindres superposés traversés par un « cylindre » creux .

Les dimensions sont en « cm ».

On vous demande de calculer le volume de cette bobine ( : quantité de matière qui constitue cette bobine ).

Volume du cylindre du dessus en « cm ³ ».

 3,14 x …30 ..² x …5 ….= …14 130….

Volume du cylindre central en «  cm³ » :

3,14 x …10 .² x …40 …..= …12 560……..

Volume du cylindre creux : 

3,14  x …5…² x …50….= …3 925….

Volume de la bobine en « c m ³ » .

 (2 x ……14 130……… + ………12 560…….) - ……3 925……….= ………36 895 cm ³………..

F8 : Situations problèmes sur le cylindre…….

Problème 1 :

Une ligne électrique de  30 km de long est constituée par 3 fils de cuivre de 1cm de diamètre.

Quelle est la masse de ces fils sachant que la masse  volumique du cuivre est de «  9 kg / dm³ »

Problème 2 :

Un bassin en ciment à la forme de la figure ci-contre.

L’épaisseur des parois et du fond est de 20 cm.

Calculez le volume de la maçonnerie ?

(Cela revient à rechercher la quantité de matière ciment plus sable ..)

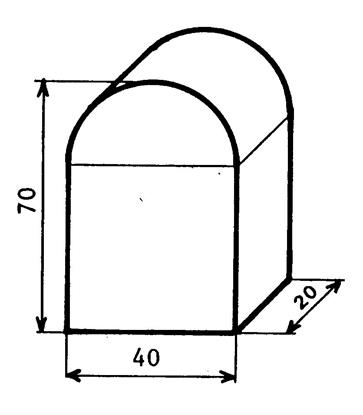
Problème 3 :

Une borne est constituée par un parallélépipède rectangle surmonté d’un demi-cylindre.

Les dimensions de la figure ci-contre  sont en « cm ».

Calculez le volume de la borne..

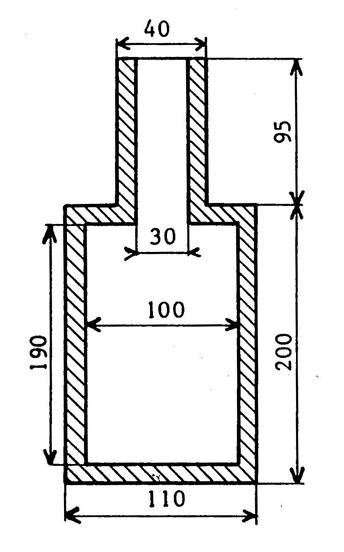
Problème 4 :

Le dessin ci-contre représente un flacon cylindrique en verre vu en coupe ..

Les dimensions sont en « mm »..

L’épaisseur du verre est de « 5 mm ».

Calculez le volume en verre utilisé pour faire ce flacon.

Problème 5 :

Un lingot de cuivre pèse « 84,78 kg » .

1°)Sachant que la masse volumique du cuivre est d’environ « 9 kg / dm³» quel est le volume de ce lingot ?

2°) Le cuivre étant très ductile , avec ce lingot, on veut fabriquer un fil cylindrique de « 1 mm » de diamètre.

Quelle longueur de fil obtiendra-t-on  ( en km) ?   ( prendre pi = 3,14 )

F9 Représentation graphique.  (niveau + facultatif)

On a mesuré ( en cm ) la longueur des arêtes de 10 cubes.

Ci-dessous on vous donne la liste :

0,5

1

1,6

2

3

3,7

4

4,5

5

6

Complétez le tableau donnant pour chaque cube :

·       Ligne « L » :  La longueur totale des arêtes (mesure en cm) ..

·       Ligne « A » : l’ aire de la surface totale ( mesure en cm² ).

·       Ligne « V » : le volume  en cm³ ..

1°

C

0,5

1

1,6

2

3

3,7

4

4,5

5

6

2°

L

6

12

19,2

24

36

44,4

48

54

60

72

3°

A

1,5

6

15,36

24

36

82,14

96

121,5

150

216

4°

V

0,125

1

4,086

8

27

50,653

64

91,125

125

216

1°) A chaque mesure de l’arête d’un cube on vous demande de faire correspondre la mesure de la longueur totale des arêtes  .(ligne 1 et 2)

On vous demande de faire la représentation graphique « en rouge » sur la page « annexe »

Co :   Longueur des arêtes :un cube à 12 arêtes.

·       Que pouvez-vous dire des points que vous venez de placer ? ……………………………………………..

·       Tracez en rouge une ligne régulière  joignant ces points. Cette ligne est une …………………………………

2°) A chaque mesure de l’arête d’un cube, on vous demande de faire correspondre la mesure de l’aire de la surface totale. ( ligne 1 et 3).

Ensuite on vous demande de faire la représentation graphique en vert  sur la même page annexe.

Co :   le calcul est égal à 6 fois le carré du côté…….

·       Les points que vous venez de placer sont-ils alignés ?................................

·       Tracez en vert une ligne régulière passant par ces points……..

·       Y-a-t-il proportionnalité entre la ligne « 1 » et la ligne « 3 » du tableau ? … (il faut calculer le coefficient de proportionnalité. En divisant .. « 1,5 / 0,5 = 3 » ; 6 ; ( 15,36 / 1,6 = 9,6 ) …….il n’y a pas de situation proportionnelle……

3°) A chaque mesure de l’arête du cube, vous devez faire correspondre  la mesure du volume  ( « 1 » et « 4 »  lignes du tableau ).

Faîtes la représentation graphique en bleu au même emplacement que précédemment.

·       Tracez en bleu une ligne régulière passant par ces points.

·       Y-a-t-il proportionnalité entre la ligne « 1 » et la ligne « 4 »  du tableau ? ………………..

4°) En utilisant la représentation graphique ( sans faire de calcul) complétez :

Longueur de l’arête

2,5 cm

4,2 cm

……de la longueur totale des arêtes

Valeur approchée

………de l’aire de la surface totale

…………………………. du volume

5°) Toujours en utilisant la représentation graphique , complète le tableau :

Mesure en « cm » de la longueur de l’arête

Mesure en « cm » de la longueur totale des arêtes

16

Mesure en « cm² » de l’aire de la surface totale.

47

Mesure en « cm³ » du volume.

157

Annexe :