|
|
|
Classe de 5ème collège |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
ENVIRONNEMENT du dossier:
DOSSIER :
|
|
LE PRISME
DROIT et OBLIQUE – la perspective cavalière (tracés)- le cylindre. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Fiche 6 : Dessin de prismes et cylindre en perspective cavalière. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
TEST |
COURS |
Interdisciplinarité |
|
||||
|
|
|
Travaux niv VI et V: Dos
191 |
|
|
|||
INFO COURS : LE PRISME
DROIT et OBLIQUE
|
|
Fiche 1
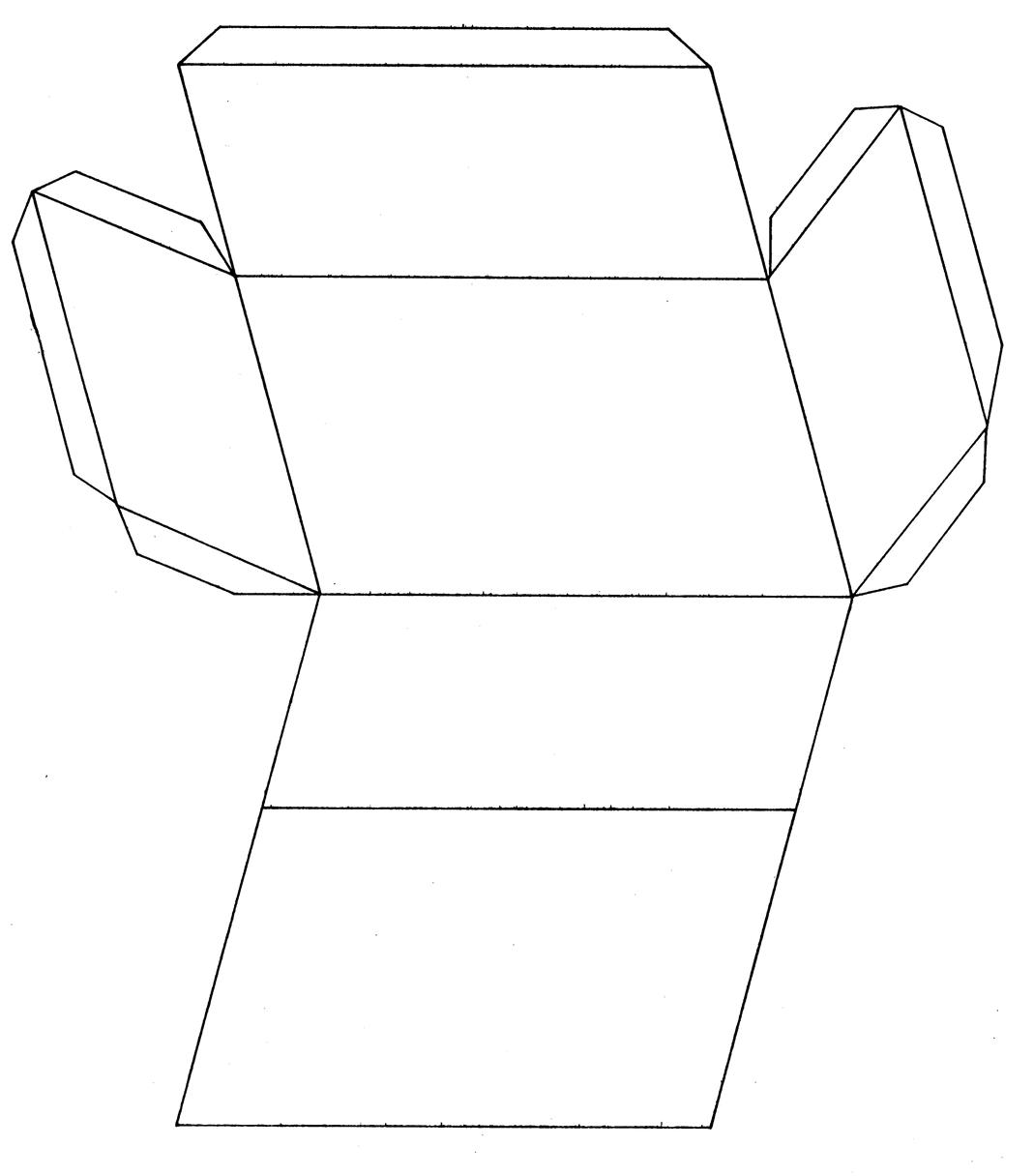
: Prisme droit à base triangulaire. ( construction : voir le
patron en fin de ces documents en annexe feuille 1) |
|
||||
|
|
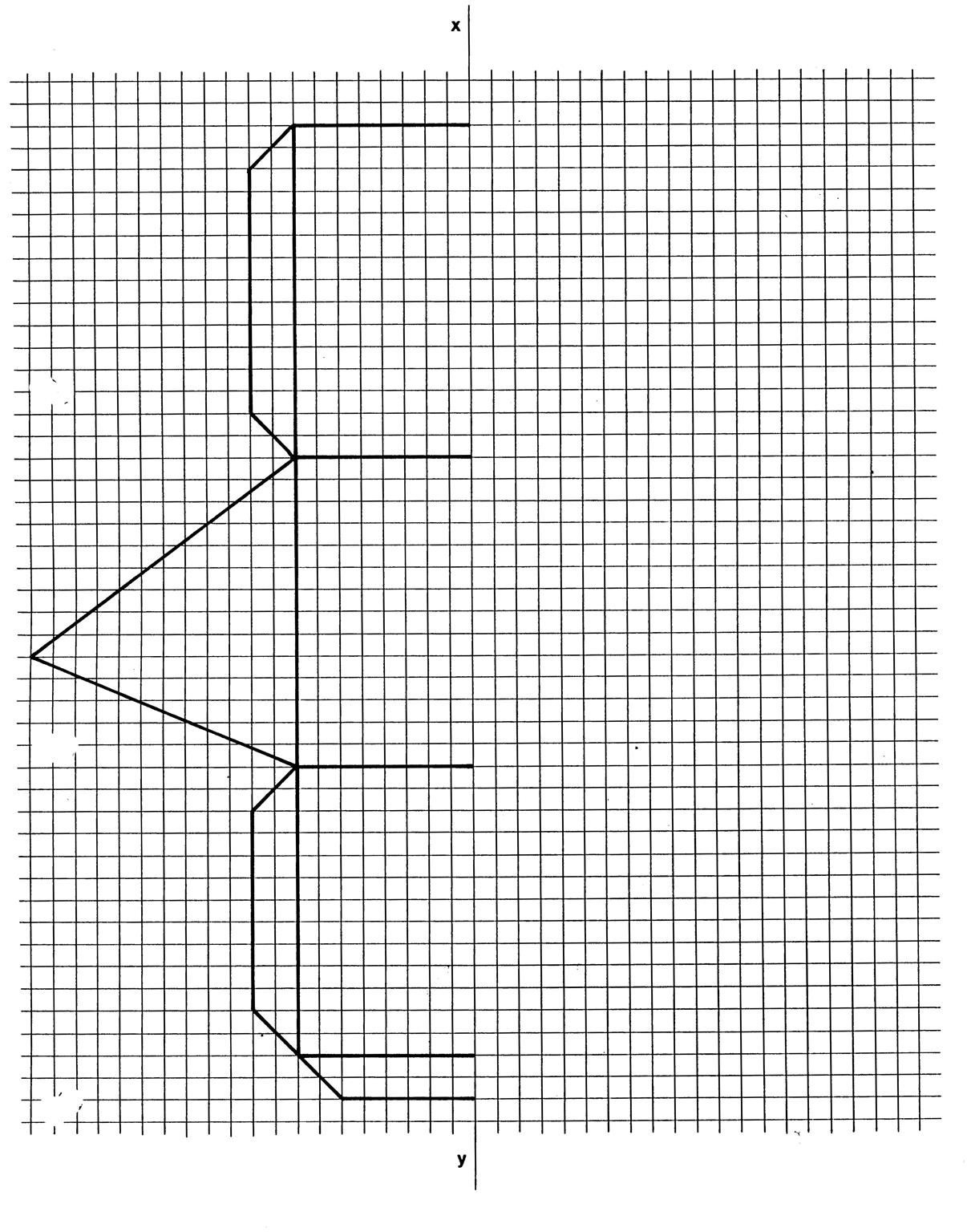
On
vous demande de fabriquer un prisme droit à base triangulaire. Pour
cela complétez le dessin (Annexe : feuille
image 1 ) de telle
sorte que la droite « xy » soit axe de
symétrie de la figure. Vous
obtenez un patron du prisme. Vous
obtenez un patron de prisme . Découpez
–le. Pliez
–le Collez
–le . ( convenablement avec les languettes) Attention : Faites en sorte que le quadrillage soit
apparent. Conservez ce prisme pour la leçon destinée à calculer le volume
(fiche 3) .. |
|
|
|||
|
|
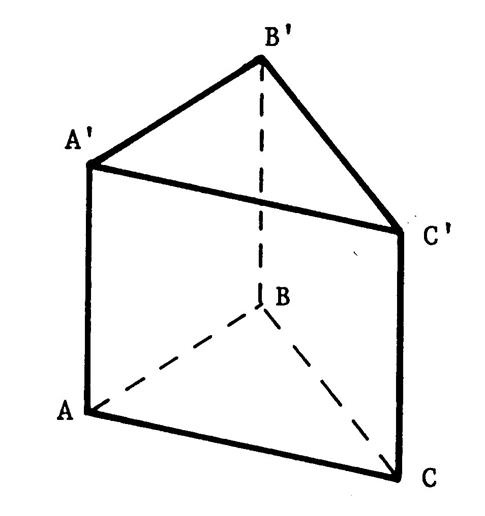
Description du
prisme : |
|
||||
|
|
La figure ci-dessus est la représentation de ce prisme en perspective cavalière.. |
|
||||
|
|
|
|
||||
|
|
Ø Les surfaces « ABC »
et « A’B’C’ » sont appelées les bases du prisme. |
|
||||
|
|
Que pouvez-vous dire de ces bases quant à leur forme ? …………………………. |
|
||||
|
|
Que
pouvez-vous dire quant à la position
des plans de ces deux bases ?
…………………………………... |
|
||||
|
|
|
|
||||
|
|
Ø Les surfaces telles que « CA A’C’ » sont appelées « faces latérales » |
|
||||
|
|
|
Nommez
les autres faces latérales de ce prisme : ……… « A’B’
BA » et « B’C’ C B » Combien
en trouvez-Vous ? ……. …… Que pouvez-vous dire des ces faces quant à leur forme ? ……………… … |
|
|||
|
|
|
|
||||
|
|
Ø Comme pour le parallélépipède rectangle , on
peut parler de sommets et d’arêtes . |
|
||||
|
|
|
Combien y a-t-il de sommets ? … … Combien y a-t-il d’arêtes ? ………… |
|
|||
|
|
|
|
||||
|
|
Ø [ A A’ ] est appelée
« arête latérale » . |
|
||||
|
|
|
Nommez les autres arêtes latérales. …………………. Que peut-on dire de n’importe quelle arête latérale par rapport aux
plans de bases ? ……………… …… Que peut-on dire du plan de chaque face latérale par rapport aux plans de
bases ? …………….. ………… |
|
|||
|
|
|
|
||||
|
|
Ø C’est la raison pour
laquelle on dit que le prisme est un prisme droite . |
|
||||
|
|
|
|
||||
|
|
A l’aide des points de la figure : |
|
||||
|
|
· Nommez 6 droites perpendiculaires à ( A A’ ) : …………………………………………………………………….. · Nommez des droites non coplanaires : ……………………………………………………………………….. · Nommez des exemples d’ une droite parallèle à
un plan. ………………………………….. ….……….. |
|
||||
|
|
|
|
||||
|
|
Aire latérale d’un prisme : |
|
||||
|
|
On appelle
« aire latérale » d’un prisme la somme des aires de ses faces
latérales. |
|
||||
|
|
|
|
||||
|
|
Activité n° … |
|
||||
|
|
Calculez l’aire latérale du prisme que vous venez de construire. ( prenez les dimensions sur
le prisme : les carrés font 5 mm de côté) |
|
||||
|
|
|
|
||||
|
|
Aire totale du
prisme : |
|
||||
|
|
On appelle « aire totale du prisme » la
somme de l’aire latérale et de l’aire des deux bases. |
|
||||
|
|
|
|
||||
|
|
Activité n°….. |
|
||||
|
|
Calculez l’aire totale du prisme que vous venez de construire
. |
|
||||
|
|
|
|
||||
|
|
Fiche 2 : Un autre prisme droite |
|
||||
|
|
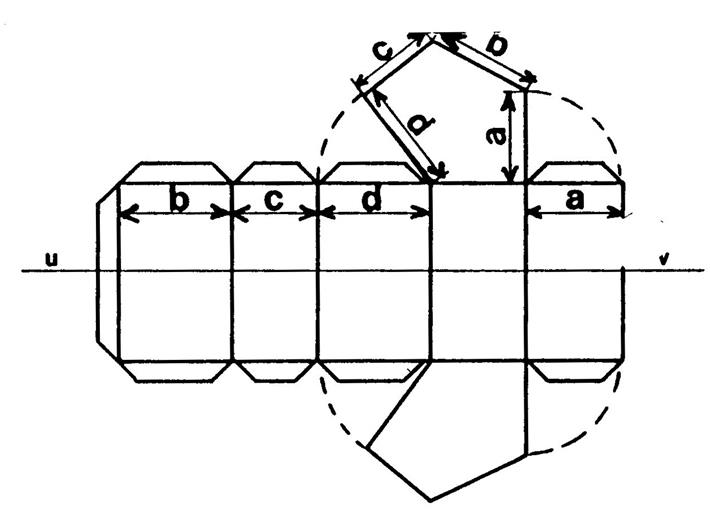
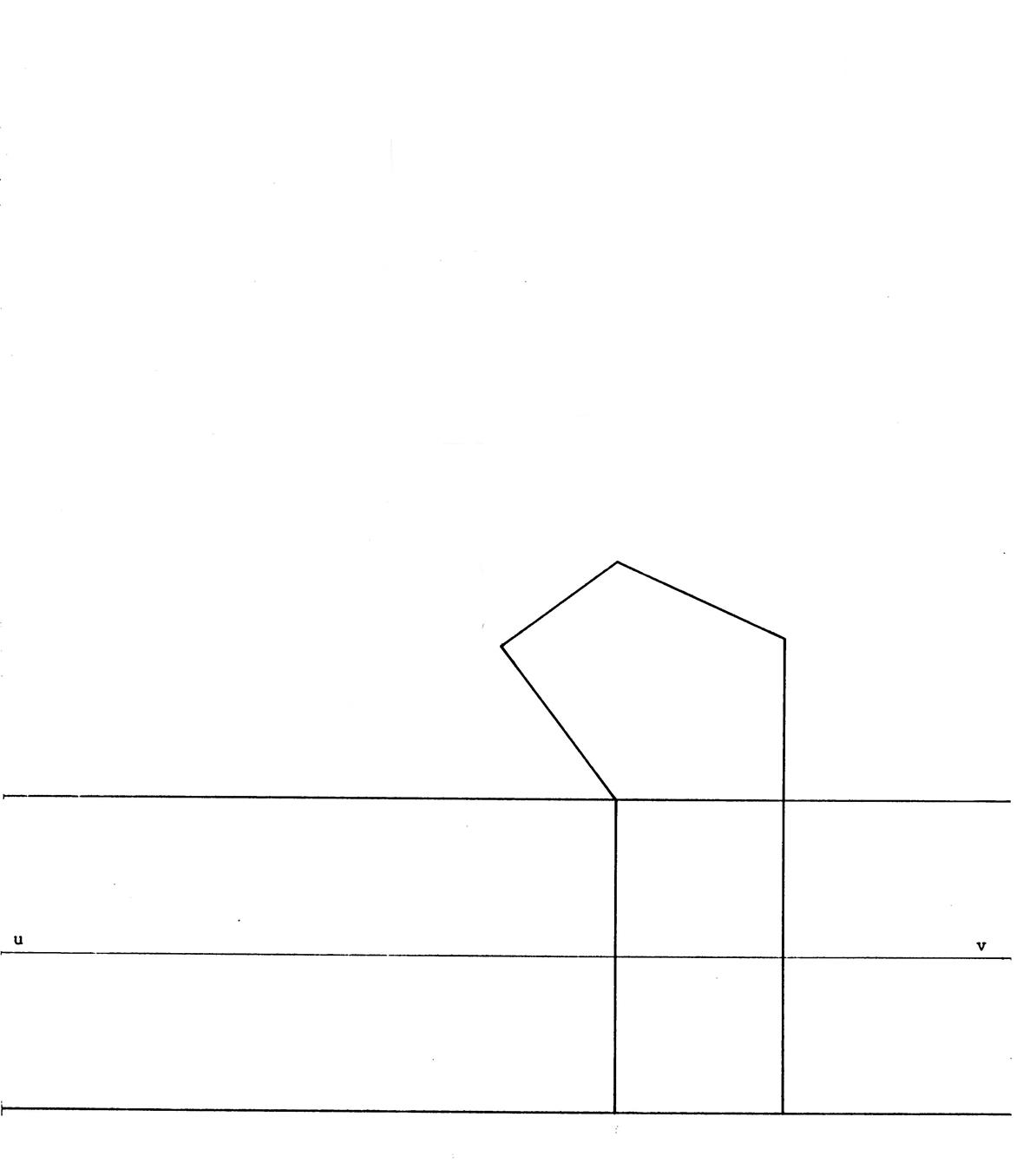
Vous allez fabriquer un prisme droit à base pentagonale. Compétez le dessin ( annexe :de la
feuille 2) de telle sorte que la droite
( uv ) soit axe de symétrie de la figure.
(voir ci-contre). Ensuite en utilisant votre compas , reporte
correctement les longueurs "a" ; "b"; "c" ;
"d"« . Terminez la figure afin qu’elle ressemble à la figure ci-contre. Vous avez obtenu le patron d’un prisme. ( bien sur
, ne dessinez pas les flèches et n'écrivez pas "a" ; "b";
"c" ; "d".) N’oubliez pas de dessiner les languettes .
Découpez le patron . Attention : conservez le
prisme pour la fiche …… |
|
|
|||
|
|
|
|
||||
|
|
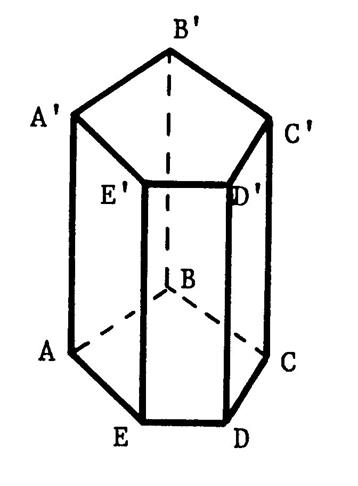
La figure ci-contre est une représentation de ce prisme en perspective
cavalière. Nommez les bases de ce prisme : ………………………………….. Que pouvez- vous dire ce ces bases quant à
leur forme ? ………………………………………………………………………. Nommez les faces latérales : …………………………………………….. …. …………………………………………………………………………….. Que pouvez-vous dire de ces faces quant à leur forme ? ……………… |
|
|
|||
|
|
|
|
||||
|
|
Pour conclure : |
|
||||
|
|
· D’une manière générale , dans tout prisme
droit , il y a deux bases , les plans de ces bases sont …………………..….. · Les bases sont superposables , ce sont des
polygones : triangle , quadrilatère , etc… · Les faces latérales sont des …………………….…. · Leur plan est ……………………………… aux plans de bases. · DE plus les arêtes latérales ont même ……………………………… |
|
||||
|
|
|
|
||||
|
|
|
|
||||
|
|
Fabriquez un prisme oblique en utilisant le patron de « l’annexe
feuille 3 » |
|
||||
|
|
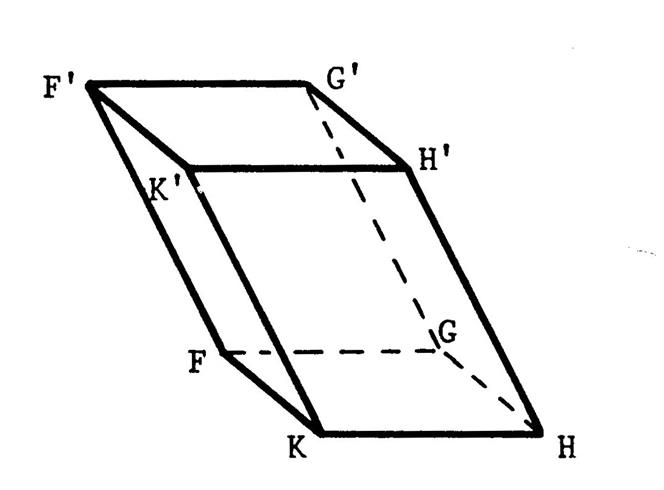
La figure ci-contre est une représentation de ce prisme oblique en
perspective cavalière. · Combien a-t-il de sommets ? ……………… · Combien a-t-il de faces ? ……. …… · Combien a-t-il d’arêtes ? …….…… · Que pouvez- vous dire de ces faces quant à leur forme ? …………………………………………………………… |
|
|
|||
|
|
Conclusion : · Dans tout prisme oblique il y a deux bases ,
les plans de ces bases sont parallèles. · Les faces latérales sont des parallélogrammes. · Leur plan n’est en général pas perpendiculaire aux
plan de bases. · Les arêtes ne sont pas perpendiculaires aux plans des bases. · Mais elles sont parallèles entre elles et ont même longueur
. |
|
||||
|
|
|
|
||||
|
|
Activité n° ….. : |
|
||||
|
|
A l’aide des points de la figure représentant le pavé oblique que vous
avez construit , · Nommez des plans parallèles :……………………………………..
….…………………….. · Nommez des droites parallèles : ……………… ………………………………………….. · Nommez des exemples d’une droite parallèle à un plan : …………………………………..…………………………… · Nommez des droites non coplanaires : …………………………………………………………… |
|
||||
|
|
Y a-t-il des droites perpendiculaires ? ………………………………………. ………………………………… ………… des plans perpendiculaires ? ……………………… …………………………… ………………des droites et des plans perpendiculaires ? ………… …………….. |
|
||||
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
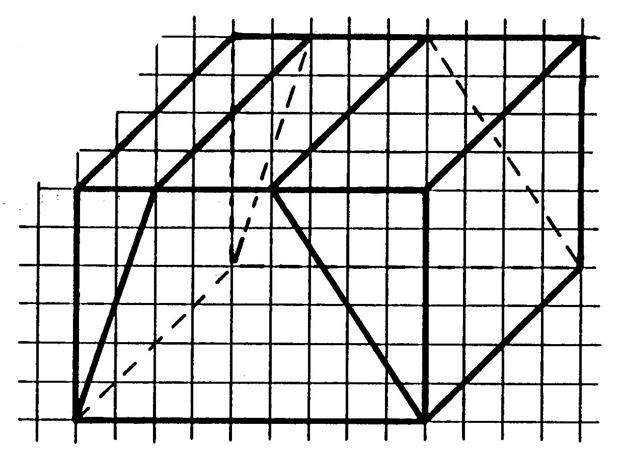
Ci-contre on vous a dessiné un parallélépipède rectangle représenté en
perspective cavalière. On a coupé ce solide de telle sorte qu’il apparaisse trois
prismes : deux à base
triangulaire et un à base
trapézoïdale. |
|
|
|
|
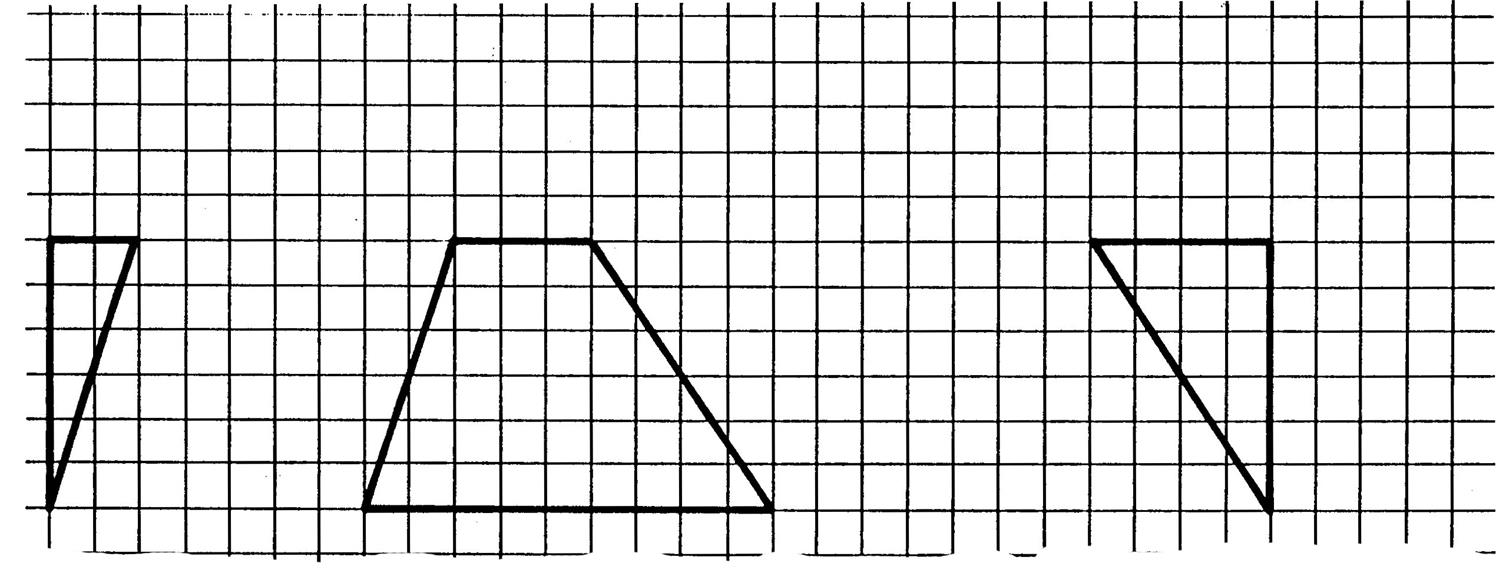
Activité n° …. On vous demande de dessiner ces trois prismes en perspective cavalière
dans la même position que ci-dessus , mais écartés
les uns et les autres. ( N’oubliez pas les traits en
pointillé représentant une arête cachée..) . On vous donne les dessins de la vue de face (vu avant ). Coloriez en couleur une base de chaque prisme. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Activité n°….. |
|
|
|
|
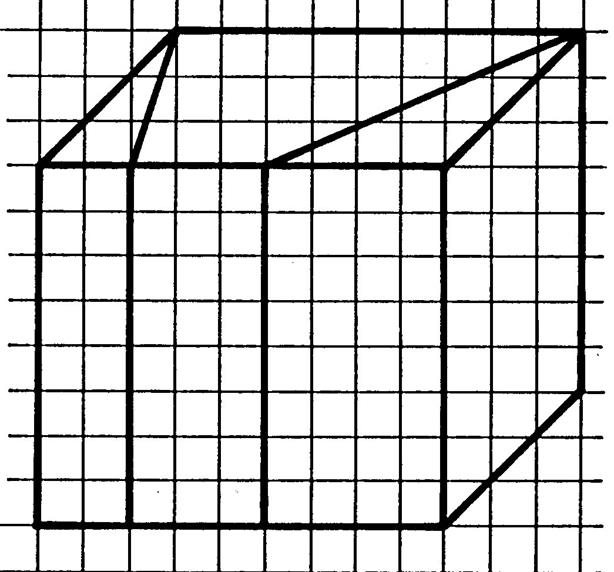
Ci-contre on a décidé de
disposer différemment le parallélépipède rectangle, mais il est
« découpé » de la même façon. |
|
|
|
|
Complétez le dessin ci-contre en plaçant les pointillés représentants
les arêtes cachées. |
|
|
|
|
|
|
|
|
|
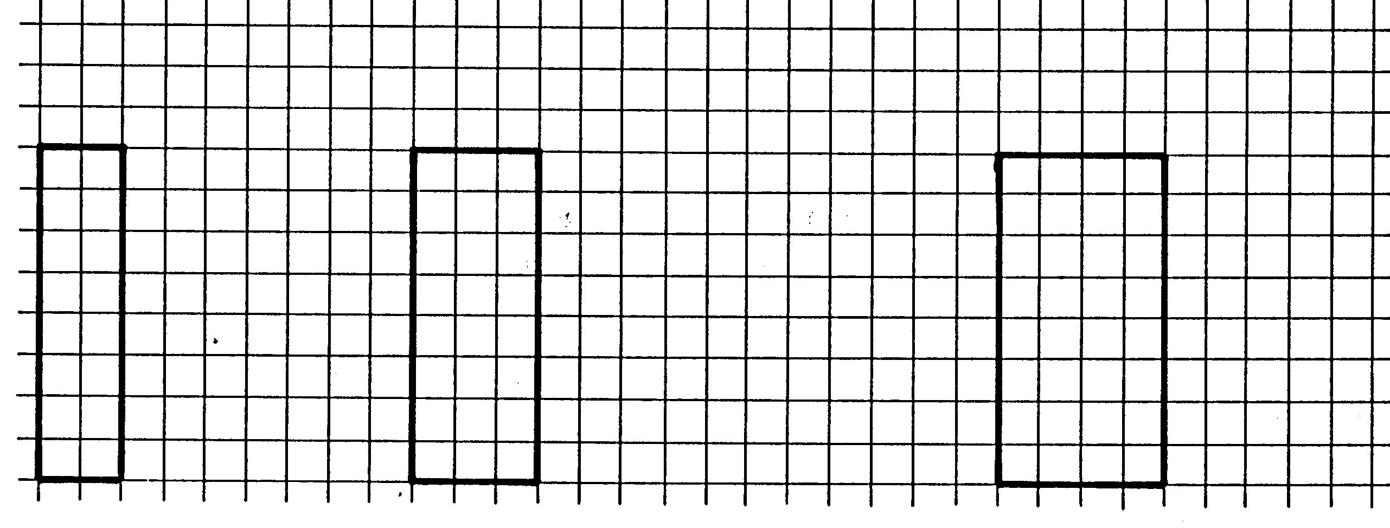
Ci-dessous , dessinez en perspective en
perspective cavalière les trois prismes placés dans cette nouvelle position . N’oubliez pas les pointillés. On vous donne le dessin en vue de face ( face
avant) Passez en couleur une base de chaque prisme. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
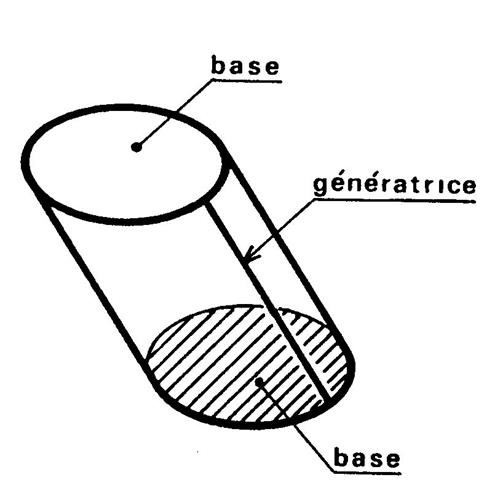
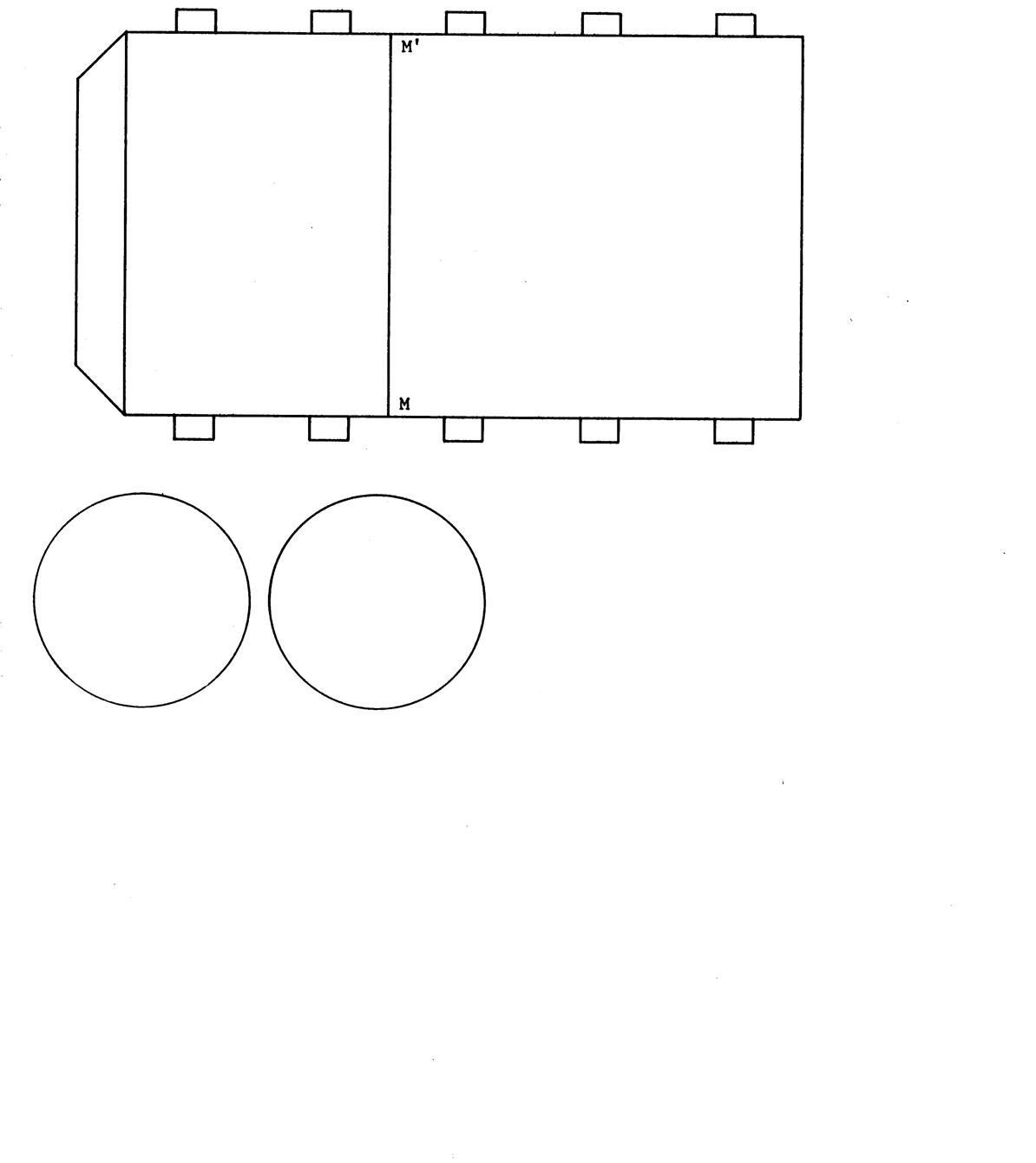
Vous allez fabriquer un cylindre de révolution en utilisant le patron
« annexe feuille 3 ». Ce patron est constitué par un rectangle ( avec
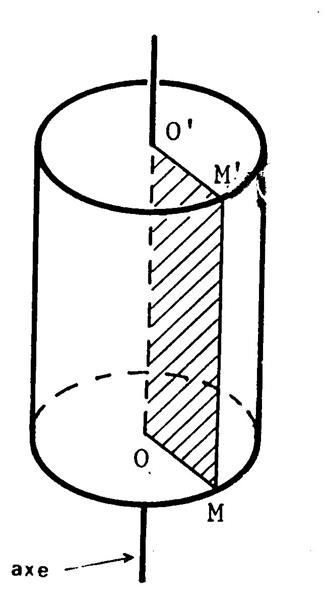
les languettes) et par deux disques qui sont les bases du cylindre.. Que pouvez-vous dire des plans des bases :….. …………………... Bien entendu , la figure ci-contre est
une représentation de ce cylindre en perspective cavalière. On dit que le
cylindre est « engendré » par le rectangle « OO’ M’M »
tournant d’un tour complet sur l’axe « OO’ ». ( on dit aussi :
autour de l’axe » . Ce cylindre est un
« cylindre dit de révolution » , parce que faire un tour complet c’est aussi dire « faire une révolution »….. |
|
|
|
|
· Le segment [ M M’] est appelé « génératrice ». · En tournant ,
la génératrice engendre la surface cylindrique ( la surface latérale). · Combien peut-on dessiner de génératrices avec le cylindre ? …………….. ……… Préparation de l’oral : Expliquez comment elles sont disposées sur le patron : ……………………………………..….. Toutes les génératrices sont ……………….…
entre elles et on la même ……………… …. Cette longueur est appelé « la hauteur » du cylindre .C’est
la distance des deux plans des bases. |
|
|
|
|
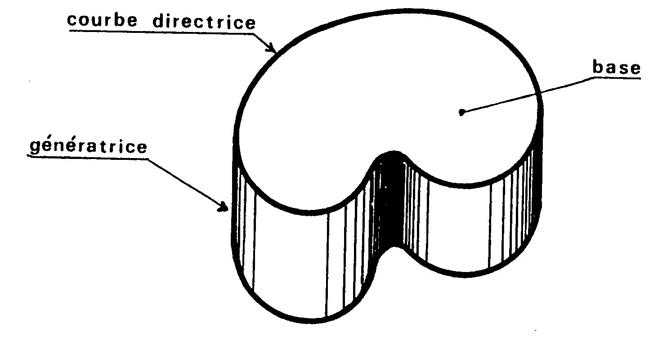
Ci-dessous est représenté deux cylindres qui ne sont pas des cylindres de révolution. |
|
|
|
|
|
|
|
|
|
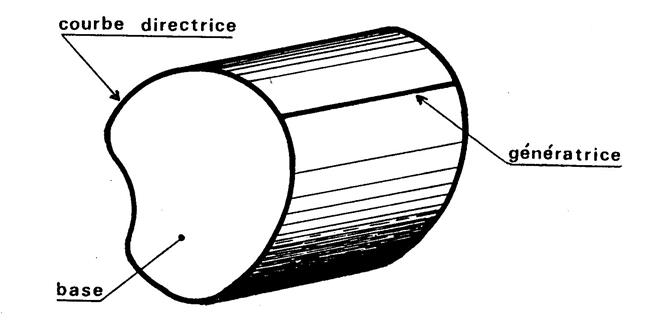
La surface latérale de ces cylindres est engendrée par un segment
(génératrice)..se déplaçant parallèlement à lui-même
en s’appuyant sur une courbe appelée « directrice ». Cette courbe est la frontière de la base du cylindre. |
|
|
|
|
|
|
|
|
|
Remarque : Dans le cas
d’un cylindre de révolution la courbe directrice est un …………………..…. |
|
|
|
|
|
|
|
|
|
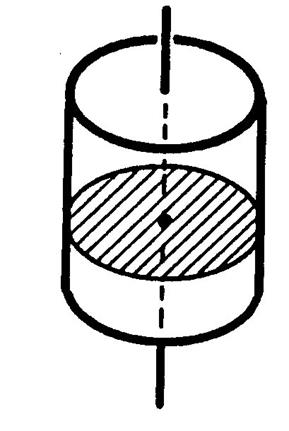
· Le cylindre de révolution peut-être aussi être engendré par un disque
qui se déplace parallèlement à son
plan de base et de telle sorte que son centre reste situé sur l’axe du cylindre . |
|
|
|
|
Cylindre oblique : Dans les exemples ci-dessus on a représenté des cylindres droits. Cela signifie que la génératrice est perpendiculaire aux plans des
bases. Ci-contre on vous a représenté un cylindre oblique. La génératrice
n’est pas perpendiculaire aux plans de bases. |
|
|
|
|
|
|
|
|
|
Situation problème n°1 : |
|
|
|
|
Vous voulez fabriquer un tuyau cylindrique de 1, 5 m de long et de 20
cm de diamètre. La plaque sera soudée en bord à bord ( pensez à une génératrice) Quelle est en
cm² l’aire de la tôle qu’il faudra
utiliser ? ( prendre « pi = 3,14) |
|
|
|
|
Situation problème n°2 : |
|
|
|
|
Vous voulez fabriquer un tuyau cylindrique de 1, 5 m de long et de 20
cm de diamètre. Pour souder la plaque on
superposera par recouvrement la plaque
de 1 cm sur toute la longueur . Quelle est en cm² l’aire de la tôle qu’il faudra
utiliser ? ( prendre « pi = 3,14) |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
Fiche
6 : Dessin de prismes et cylindre en perspective cavalière. |
|
||
|
|
|
|
||
|
|
On vous demande de dessiner en perspective cavalière les 2 prismes et
un cylindre. |
|
||
|
|
|
|
||
|
|
|
|
|
|
|
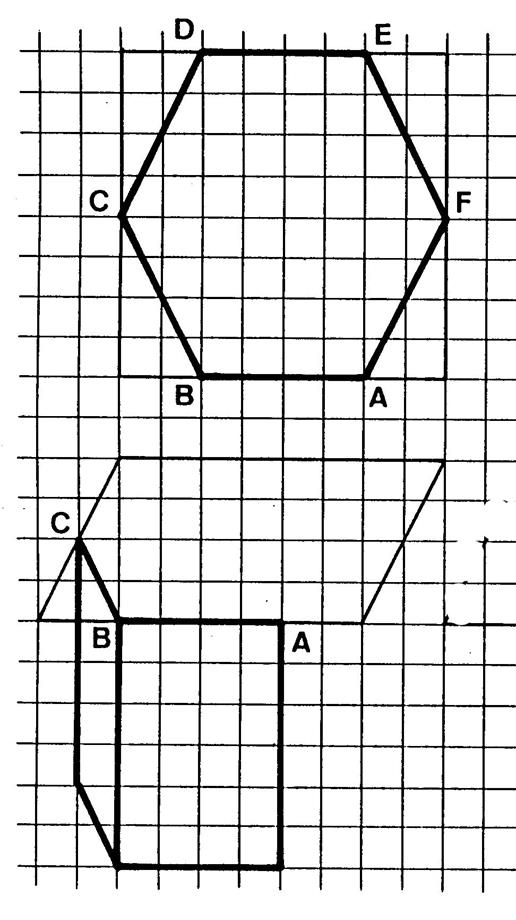
On a représenté ci-contre , en vraie
grandeur, la base d’un prisme. C’est un hexagonal (non régulier) . Il est inscrit dans un carré. En dessous, on a représenté ce carré en perspective cavalière et on a placé
les sommets « A » , « B » et
« C » de l’hexagone. A vous de placer les autres sommets en tenant compte de leur position
sur le carré. ( utilisez le quadrillage) . Puis terminez le dessin du prisme. ( On a déjà dessiné deux
faces latérales). N’oubliez pas les pointillés. |
|
|||
|
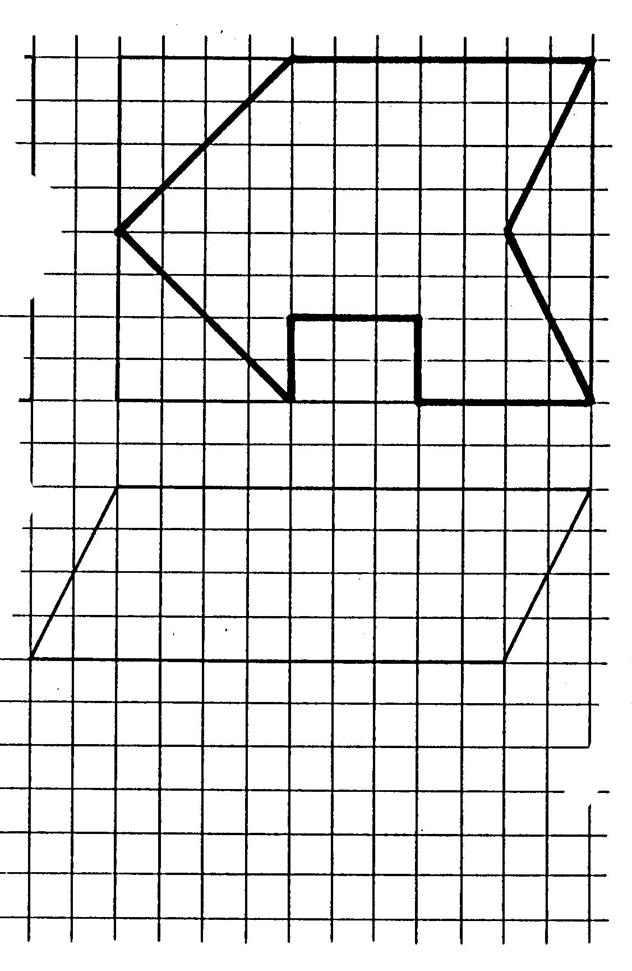
Faîtes de même pour le prisme dont on donne la base en vraie grandeur.. Cette base est inscrite dans un rectangle dont on donne
, en dessous , le dessin en perspective cavalière . Le prisme a 3 cm de haut. |
|
|||
|
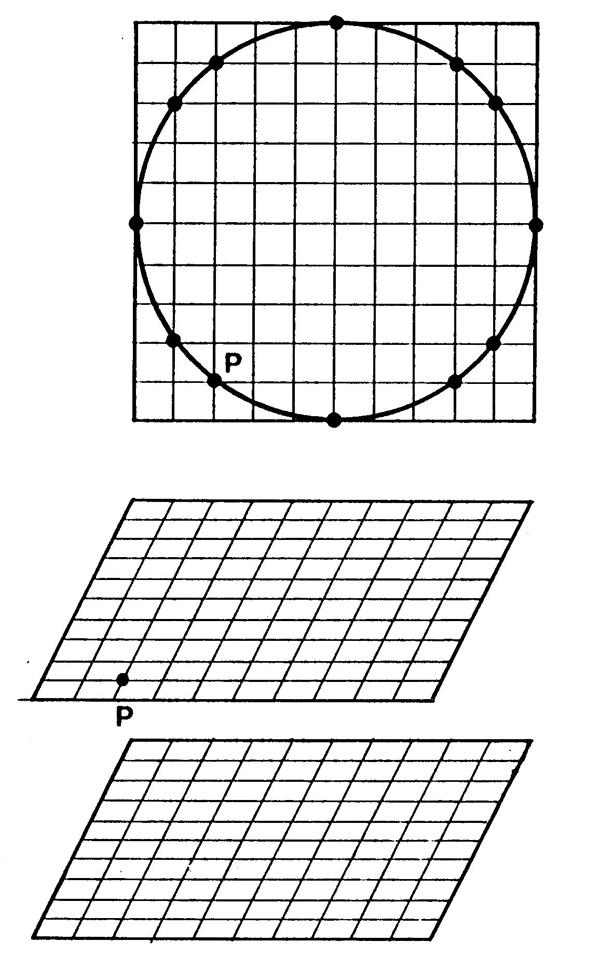
Voir les dessins ci-contre : On a représenté , en vraie grandeur , la base
d’un cylindre , c’est un cercle.( il
est inscrit dans un carré quadrillé ) En dessous , on a représenté ce carré et son
quadrillage en perspective cavalière. Ceci va vous permettre de déterminer le dessin des bases en
perspective cavalière. Pour cela , commencez par placer les 12
points marqués sur le cercle ( on a déjà placé le point « P » puis
tracez la courbe passant par ces 12 points ( c’est une ellipse). Puis terminez le dessin de ce cylindre. |
|
|||
|
|
|
|
|||||||||||
|
|
Fiche 7 : Représentation graphique. |
|
|||||||||||
|
|
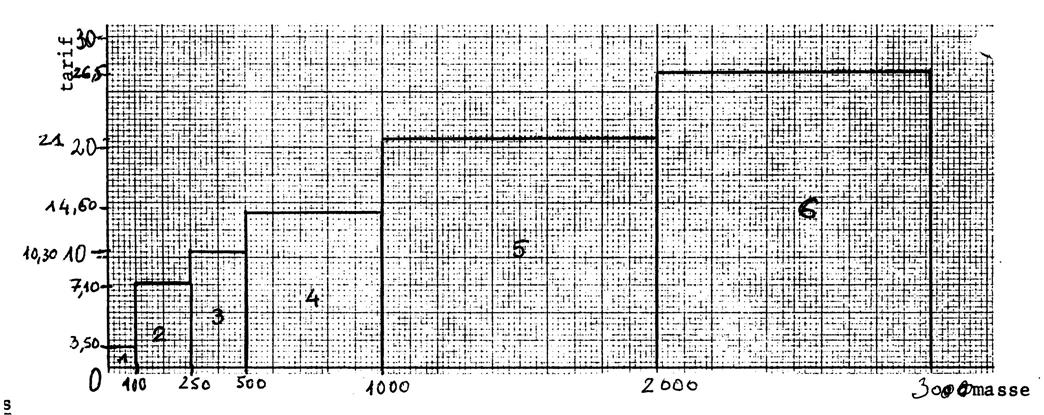
Le tableau ci-dessous donne les tarifs exigés pour le transport des
paquets-poste contenant des objets fragiles
en fonction le leur masse
(jusqu’à 3 000 grammes ,(« gramme » pour
lettre « g » ). La lettre « m » désigne la masse du paquet en « g » . |
|
|||||||||||
|
|
Masse en «g » |
m |
100 |
250 |
500 |
1000 |
2000 |
|
|
|
|||
|
Tarif en « € » |
3,50 |
7,10 |
10,30 |
14,60 |
21,00 |
26,50 |
|
|
|||||
|
|
|
|
|||||||||||
|
|
On vous demande de faire la représentation graphique correspondante. |
|
|||||||||||
|
|
Conseil : commencez par
choisir convenablement les unités sur les axes. (voir info cours
précédent sur le repérage et les graduations ).afin d’utiliser au maximum les graduations des axes tracés
ci-dessous. |
|
|||||||||||
|
|
Attention : Le graphique
que vous devez dessiner est différent de ceux que vous avez faits jusqu'à ce
jour. Vous n’allez pas
obtenir une courbe continue mais une succession de segments disposés en
escalier. |
|
|||||||||||
|
|
Exemple : Entre « 1 000 g »
et « 2 000g » , le tarif est
de 21 € , c'est-à-dire que pour une paquet de 1150g ; 1550 g ; 1875
g (par exemple)le tarif est de 21 €. Les points correspondants ont donc « la même ordonnée ». Ils sont donc situés sur un segment parallèle à l’axe des abscisses. |
|
|||||||||||
|
|
|
|
|||||||||||
|
|
|
|
|||||||||||
|
|
Questions : |
|
|||||||||||
|
|
1°) Le tarif d’affranchissement est –il proportionnel à la masse du paquet ? …… …. 2°) Quel est le tarif pour : |
|
|||||||||||
|
|
135 g = ……………€ |
730 g = ……….……€ |
2,650 g = ………………….€ |
|
|||||||||
|
|
|
|
|||||||||||
|
|
3°) On dispose de 18 € pour
payer le transport d’un paquet. Quelle est la masse maximum du paquet que l’on peut expédier ? ……………. …. |
|
|||||||||||
|
|
4°) On veut expédier à une même personne 2 objets pesant chacun « 100 g » ( emballage compris). Pour que le prix soit le moins élevé possible, doit-on faire un paquet
ou deux paquets ? (expliquez) |
|
|||||||||||
|
|
5°) On veut expédier à une même personne 6 objets pesant chacun 100 g ( emballage compris)
. Pour que le prix soit le moins élevé possible doit-on faire un ou plusieurs
paquets ? (
expliquez) . |
|
|||||||||||
|
|
|
|
|||||||||||
|
|
6°) Même question pour 6 objets pesant chacun 200 g
. |
|
|||||||||||
|
|
|
||||||||||||
|
|
|
|
|||||||||||
|
|
ANNEXES :
( 3 feuilles ) |
Retour aux documents : cours sur les prismes
et la perspective cavalière. |
|
||||||||||
|
|
(feuille image1 ) |
|
|
|
|
|
|
|
Feuille 2 |
|
|
|
|
|
|
|
|
|
|
|
Feuille 3 |
|
|
|
|
|
|
|
|
|
|
Feuille
4 |
|
|
|
|
|
|
|
|
|
CONTROLE :
1° ) Quand dit-on qu’un
prisme est droit ? (donnez ce qui le caractérise) .
2°) Quelle est la forme des surfaces
latérales ?
3°) Qu’est ce qu’un
parallélépipède droit ?:
4°) Qu’est ce qu’un parallélépipède droit ?:
1 ) Dessiner un
prisme droit.
1)
Un
bassin de 3 m² est alimenté par un robinet. On ouvre le robinet une demi-heure
Le niveau de l’eau monte alors de 90 cm.
Quel est le volume du
bassin ?débit du robinet ?
1. 1.5 l / s
2. 9 m3 / h
3.
15 l / min
4.
540 l /h
Réponse : volume d’eau contenu dans le bassin
après une demi-heure : 3 fois 0,9 = 2, 7 m3
Débit : 2700 : 3O = 90 l/mn