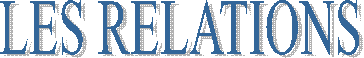Auteur : WARME R.

INFORMATIONS  « LIVRE ».

NOM : ………………………………

Prénom : …………………………..

Classe :…………………..

Année    scolaire : ………………………                                        

Dossier pris le : ……/………/………

Validation de la  formation :    O -  N

 Le : ……………………………………..

Nom du  formateur  : ……………………

ETABLISSEMENT : …………………………………………..

Leçon

Titre

N°22 /25

LES  RELATIONS  TRIGONOMETRIQUES  dans le triangle rectangle.

CHAPITRES

I ) nomenclature .terminologie  ( côté opposé , côté adjacent ,hypoténuse, sinus, cosinus, tangente) .

Cd :Info plus .

II ) DEFINITIONS des  3 principales relations trigonométriques .

Cd :Info plus .

- 1 ) Activités découvertes

-  2 ) Synthèse

-  3 ) Résumé : définition du sinus ; cosinus et tangente d’un angle.

III ) CONVERSION d’une valeur  décimale  en valeur angulaire Passage d’une valeur à l’autre .(valeur décimale d’un sin a; cos a, tan a,  en  valeur en degré de l’angle a)

Usage des tables

a) avec la calculatrice

Cd :Info plus .

b)avec la table de trigonométrie.

Cd :Info plus .

IV )Calculs d’éléments d’un triangle rectangle.

Cd :Info plus « sinus ».

1°) Recherche  d’un angle connaissant les longueurs de deux côtés.

Cd :Info plus   « cosinus » .

2°) Recherche de la longueur d’un côté  connaissant un angle et la longueur d’un autre côté .

Cd :Info plus « tangente ».

COURS

i9  et i29

I ) NOMENCLATURE et TERMINOLOGIE .

Cd :Info plus .

I - 1 )  Noms des angles dans un triangle rectangle :  ( info Cd ++)

Noms donnés  aux angles : 

 Info + Cd : le triangle rectangle et les relations trigonométriques .

Pour le symbole « b » lire « bêta » ;

 ( =  )

Pour le symbole « a »  lire « alpha » ;

 ( = )

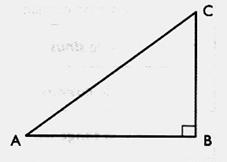
En « A » : un carré (ou rectangle) symbolise l’angle droit.

L’angle  « b » se trouve   à l’opposé  du côté AC.  ( ou CA )

L’angle  « a »  se trouve  à l’opposé du  côté AB  ( ou BA )

Les côté AB et BC sont consécutifs . ( AB est appelé le « côté adjacent » à l’angle « b »)

Les côtés AC et CB sont consécutifs. ( AC est appelé le « côté adjacent » à l’angle « a »)

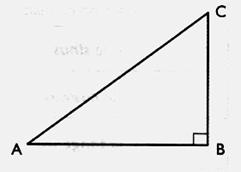
I - 2 )  Identification du « Côté opposé » , « côté adjacent » , « hypoténuse » d’un angle

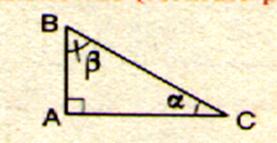
Angles :

   Le triangle rectangle possède deux angles aigus  ( en A et C )  et un angle droit  ( en B) .

Côtés : 

- le plus long côté s’appellera toujours « hypoténuse ».( exemple AC ) ;

- Le côté CB est appelé « côté opposé » à l’angle   ( qu’il ne forme pas) , il est aussi appelé  « côté adjacent » à l’angle   .

- Le côté AB est appelé « côté opposé » à l’angle   (qu’il ne forme pas) , il est aussi appelé  « côté adjacent » à l’angle    .

†        Activité 1 :

   On choisit  de se positionner à  l’angle droit :  ( on se place sur la pointe de l’angle droit )

Le côté opposé à l’angle droit s’appelle : hypoténuse . (C’est toujours le côté qui mesure la plus grande longueur. )

Ici l’hypoténuse  est  bornée par les points A et C noté [AC]  .

b)  Les  2 autres côtés  forment l’angle droit , ils ont un point commun ( B ) , ils  n’ont pas de nom particulier , tant qu ‘ il  ne  sera  pas  positionné par rapport à un sommet du triangle .

† Activité 2 :   On considère l’angle  A  ( noté :   )  ( on se place en A ! ! !)

A

A

AC :     AC est l’hypoténuse ( le +  long ) ;

CB :  on nommera  « CB »   le  côté opposé à l’ouverture  ou la fermeture de l’angle A  . ( On peut se souvenir  que si AC et AB sont les branches d’un compas articulé en A  , CB est un tige rigide qui empêche le compas de s’ouvrir ou de se fermer )

AB :      AB s’appellera «  côté adjacent » à l’angle A . 

Activité 3 :  On considère l’angle   « C » : ( on se place sur  « C » )

AC : reste  l’hypoténuse ( c’est le plus long côté)

AB :   AB s’oppose à l’ouverture ou à la fermeture de l’angle   , il s’appellera « côté opposé » .

CB : reste donc à nommer CB ; CB s’appellera « côté  adjacent » à l’angle « C ».

I - 3 )  En résumé : pour un triangle rectangle CBA ; rectangle en B :on nommera les côtés ainsi ( les 3 segments de droite formants  le triangle  , 3 côtés  pour 5 noms ):

Si l’on se fixe sur un angle ; on nommera les côtés  de la façon suivante :

Pour l’angle droit

On se place au point « B »

Pour l’angle    

On se place au point « A »

Pour l’angle    

On se place au point   « C »

AC

est appelé :

Côté opposé à 90° :   Hypoténuse

Hypoténuse

Hypoténuse

AB

est appelé

côté adjacent  à 90°

Côté adjacent (à )

Côté  opposé   ( à )

BC

est appelé

côté adjacent  à 90°

Côté opposé  ( à )

Côté adjacent   ( à )

i9

II - 1  ) Activités  « découverte »

i  La relation trigonométrique  de chaque relation dépend du calcul effectué.

Pour chaque angle aigu   et    on peut déterminer  par calculs * 3 nombres décimaux différents appelés :  l’un « sinus »  l’autre « cosinus »            et un suivant  « tangente ».

*(Ces calculs sont des divisions de deux  longueurs de deux côtés  judicieusement choisis dans le triangle rectangle .)

Pour connaître ces calculs  faites  l’activité suivante ! ! !:

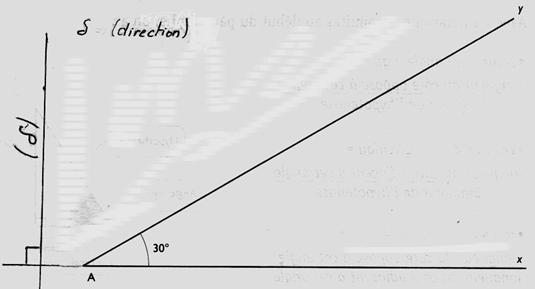
†  ACTIVITE 4 :

On vous donne  ( les données sont … ;) :

Sur la figure suivante sont dessinées deux demi-droites ( A x et Ay )sécantes en A formant un angle de 30°. et une troisième  droite de direction  orthogonale à la demi-droite Ax .

On vous demande de faire ( effectuer les tracés …) :

a)  On demande  de  placer sur la demi-droite  Ay   le point  « B » à 100 mm , « C » à  60 mm et  un point  « M »  éloigné  entre « A » et « B » à plus de 20 mm de « C »  . 

b) Tracer  les points ( appelés : projetés orthogonaux)   « B’ »   « M’ »  et « C’ »  sur la demi-droite  Ax .

c)  Observations : 

iOn doit obtenir  trois triangles rectangles : AB B’ , AC C’ , et AM M’

=Vérifier que ces triangles sont rectangles : pour cela tracer des cercles dont les centre se trouvent sur Ay et dont le centre de chaque cercle est le milieu des segments  AB , AC et AM.

Ces triangles ont  en commun l’angle  ……..qui mesure …………

† Activité 5 :

a) Mesurer les longueurs ( en mm ) sur la figure :

AB

AB’

BB’

AC

AC’

CC’

AM

AM’

MM’

100 mm

………..

………

60 mm

………..

………..

………..

………

………..

b) Compléter le tableau ( arrondir les résultats à  deux décimales ; ou à 0,01 près)

1

Le nombre obtenu est appelé le sinus de l’angle  de 30°

2

Le nombre obtenu est  appelé le cosinus de l’angle  de 30°

3

Le nombre obtenu est appelé  le tangente de l’angle  de 30°

c ) Comparaison des résultats par ligne  :

  Les trois résultats « par ligne » doivent être égaux . Interpréter une éventuelle  différence : …………………………………………………………………………

i9

II - 2 )   Synthèse  des activités « découvertes »

:i

Généralisons au triangle rectangle  ACB   rectangle en   B :

-          les rapports   ne dépendent pas des dimensions des triangles mais seulement de leurs angles .

=par exemple :

 Le quotient du rapport  est pour l’angle   son  « sinus »  et ce même quotient  est pour l’angle    son   « cosinus ».

 C’est ainsi que l’on peut dire que le sinus de     est égal au cosinus de   ( à vérifier).  Que l’on écrit :    

Dans le triangle rectangle  CBA , rectangle en B , on aura les égalités suivantes :

-           ;  ;  

-           

-           ;  ;

i9

II - 3  )   Résumé :

:i

On retiendra  les  3  relations suivantes :

1)  Sinus d’un angle aigu               :Cd info plus

Le sinus d’un angle ( noté : sin. ) est un nombre égal au quotient du rapport de la longueur du côté opposé à cet angle sur la longueur de l’hypoténuse .   

Sin.  =

2)  Cosinus d’un angle aigu         :Cd info plus

Le cosinus d’un angle ( noté : cos. ) est un nombre égal au quotient du rapport de la longueur du côté adjacent  à cet angle sur la longueur de l’hypoténuse .      cos. =

3)  La tangente d’un angle aigu

:Cd info plus

La tangente d’un angle ( noté : tan. ) est un nombre égal au quotient du rapport de la longueur du côté opposé à cet angle sur la longueur du côté adjacent à cet angle .

tan. =

i9

II -4 )  Exemples numériques :

:i

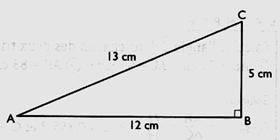
Dans le triangle rectangle ci -dessous : ( à vérifier par Pythagore )

Calculer :   ;  ;   et puis  ,   et .

Solution :

 =

  =

 =

  » 0,384 6

»  0,923 1

 »  0 , 416 7

 » 0,384 6

  »  0,923 1

  »  0 , 416 7

»  0,923 1

  » 0,384 6

  = 2,4

  »  0,923 1

  » 0,384 6

  = 2,4

On remarque  que  :

-          »  0,384 6  et    » 0,384 6  ,  il est  donc possible d’écrire que  =   

  »  0,923 1 et   »  0,923 1 ; donc   =    

i9

III )   CONVERTION  d’une valeur décimale    d’un sin a ; cos  , tan    en  valeur   angulaire  , exprimé en degré de l’angle a  ( noté :  )  et vis versa .

:i

Usage des tables

Ces conversions ne peuvent se faire  qu’en consultant  soit la calculatrice (en mode degré ), soit une table de trigonométrie .

Ainsi , lorsque je sais utiliser la calculatrice ou la table :

i  Lorsque l’on connaît la valeur décimale d ‘un sinus , d ‘un  cosinus ou d ‘ une tangente d’un angle , il est possible de convertir cette valeur décimale en  degré ( valeur angulaire) .

Inversement si je connais  la valeur ,en degré, d ‘ un  angle ,je peux ,en consultant la table numérique ou en utilisant la calculatrice obtenir  la valeur décimale du sinus ,cosinus ou tangente de cet  angle.

La suite de ce chapitre vous apprend à utiliser la calculatrice et ensuite avec la table .

Conseil important : si vous n’êtes pas sur de savoir utiliser correctement  votre calculatrice ,et pour plus de sécurité , vérifier  sur la table  , en comparant les résultats .

i9

III - 1  )  Utilisation de la calculatrice :

Cd :Info plus .

Sans calcul , on peut ,à partir  de la valeur décimale du sinus , cosinus , tangente d’un angle , trouver la valeur angulaire de cet angle ; inversement à partir d’un angle on peut obtenir sans difficulté le sinus , cosinus ou la   tangente de cet angle ( généralement c’est une valeur décimale approchée ).

A ) La valeur angulaire d’un angle aigu étant donnée ( entre 0° et 90°) .Recherche de la valeur décimale d’un sinus , cosinus et tangente  .

Cd :Info plus .

i-  Les valeurs des rapports trigonométriques ( sinus , cosinus , tangente ) d’un angle aigu sont données par la calculatrice , ou une table numérique, il suffit de savoir  connaître son mode d’emploi .

 i  -  Sur une calculatrice , les angles peuvent être exprimés en degrés décimaux , grades ou radians . ( Info plus : cliquer sur les mots )

i  -  L’unité d’angle utilisé dans ce cours est le degré décimal.

Activité 6  -  Mettre la calculatrice en mode  DEGRE  ( voir le fascicule  qui accompagne  votre calculatrice).

2°)

Pour trouver le sinus d’un angle aigu

Introduire  la mesure de l’angle  ( en degré)

Puis presser sur la touche

«  SIN »

Pour trouver le cosinus d’un angle aigu

Introduire  la mesure de l’angle  ( en degré)

Puis presser sur la touche

«  COS »

Pour trouver la tangente sinus d’un angle aigu

Introduire  la mesure de l’angle  ( en degré)

Puis presser sur la touche

«  TAN »

Exemple :

Utiliser la calculatrice pour trouver le sinus , le cosinus et tangente des angles : 7° ; 30° ; 84°.

Angle :

Sinus

Cosinus

Tangente

7°

30°

84°

( en général on arrondit au 0,001 près )

le  corrigé se trouve à la  fin du cours.

i9  

B )La valeur du sinus ou cosinus ou tangente  étant donnée , on recherche  la valeur de l’angle  en degré .

Cd :Info plus .

Préalable :  mettre la calculatrice en mode  DEGRE  ( voir le fascicule  qui accompagne  votre calculatrice).

Attention , il faut connaître les touches , les procédures et le mode d’utilisation  de votre calculatrice !.

Pour le « SINUS » :

A partir de la  valeur décimale « sinus »  pour obtenir la valeur en degré , vous devrez  appuyer sur la touche :     INV . SIN ; ou SIN^-1 ; ou ASN ; ( ces Touches remplissent la même fonction , à vous d’identifier la bonne touche.)

Pour le « COSINUS » :

A partir de la  valeur décimale « cosinus »  pour obtenir la valeur en degré , vous devrez appuyer sur la touche  INV . COS ; ou COS^-1 ; ou ACN ; ( ces Touches remplissent la même fonction, à vous d’identifier la bonne touche.)

Pour la  « TANGENTE » :

A partir de la  valeur décimale « tangente »  pour obtenir la valeur en degré  ,vous devrez appuyer sur la touche  INV . TAN ; ou TAN^-1 ; ou ATN ; ( ces Touches remplissent la même fonction, à vous d’identifier la bonne touche.)

Exemples :

1°) Utiliser la calculatrice  pour trouver l’angle  C dont le sinus est 0,876 5 .

Pour trouver la mesure de l’angle  ( en ° ) dont on connaît  le sinus d’un angle aigu procéder ainsi :

Procédure :

sinus   =  0,876 5 ;    = ?

Introduire dans la calculatrice  la valeur  du  sinus  de l’angle   .

0,876 5

Puis presser sur la touche :

« INV » et la touche «  SIN »

ou SIN^-1 ;

ou ASN

Lecture écran :             Affichage

61,22 30002674563870029460466444187°

Réponse :

sinus  0,876 5 » 61,22°

Compte rendu :

l’angle C  » 61,22°   , ou   » 61,22°

2°) Utiliser la calculatrice  pour trouver l’angle  A ( ) dont le cosinus est 0,423 6

Pour trouver la mesure de l’angle  ( en ° ) dont on connaît  le cosinus d’un angle aigu procéder ainsi :

Procédure :

cosinus   =  0,423 6  ;   = ?

Introduire dans la calculatrice  la valeur  du  cosinus  de l’angle.

0,423 6

Puis presser sur la touche :

« INV » et la touche «  COS »

ou COS^-1 ;

ou ACN

Lecture écran :                                Affichage

64,9379198941684120820136530194404

Réponse :

cosinus 0,423 6  » 64,94 °

Compte rendu :

l’angle   » 64,94 ° , ou   » 64,94 °

3°) Utiliser la calculatrice  pour trouver  l’angle  B  dont la tangente  est 1,973 2

Pour trouver la mesure de l’angle  ( en ° ) dont on connaît  la tangente  d’un angle aigu procéder ainsi :

Procédure :

Tangente    =  1, 973 2  ;   = ?

Introduire dans la calculatrice  la valeur  du  cosinus  de l’angle.

0,423 6

Puis presser sur la touche :

« INV » et la touche  «  TAN »

ou TAN^-1 ;

ou ATN

Lecture écran :                                Affichage

63,1245186381872560194775281181102

Réponse :

tangente 1,9732 » 63,12°

Compte rendu :

l’angle   » 63,12° , ou   » 63,12°

i9   

C )  UTILISATION DE LA TABLE DE TRIGONOMETRIE

Info plus  +++CD

De nombreuses tables existent , celle proposée  ,ci dessous ,est la plus simple :

Le sinus de 36° (0,5878) est égal au cosinus de 54°

1°)  Recherche du « SINUS d’un angle »  :

 A)Recherche du sinus à partir d’un angle

Avec la table.

Avec la calculatrice scientifique

1°

0,0175

0,17452406

10°

0,1736

0,1736481777

24°

0,4067

0,406736643

30°

0,500000

0,50000000

45°

0,7071

0,707106781

60°

0,8660

0,866025404

90°

1

1

B ) Recherche d’ un angle à partir d’un nombre décimal (n £ 1 )

Avec la table.

Avec la calculatrice scientifique

0,2419

14 °

Forme décimale :      13,99870707°

forme sexagésimale :  13°59’55’’35/100

0,8290

56°

55,99615045°

55°59’46’’14 /100

0,289256198

16°30’

16°48’48’’35/100

0,5

30°

0,866

59,99708907°

59°59’49’’

2°) Recherche du « COSINUS d’un angle »  :

A )Recherche du cosinus à partir d’un angle

Avec la table.

Avec la calculatrice scientifique

1°

10°

24°

0,9135

0,913545457642600895502127571985317

30°

45°

60°

90°

B ) Recherche d’ un angle à partir d’un nombre décimal (n £ 1 )

Avec la table.

Avec la calculatrice scientifique

0,2419

76

76,0012929273909452030608943275762

0,8290

0,289256198

0,5

0,866

3° ) Recherche de la « Tangente d’un angle »  :

A )Recherche d’une tangente à partir d’un angle

Avec la table.

Avec la calculatrice scientifique

1°

10°

24°

30°

0,5774

0,577350269189625764509148780501957

45°

60°

90°

B) Recherche d ’ un angle à partir d’un nombre décimal

Avec la table.

Avec la calculatrice scientifique

0,2419

Entre 13 et 14°

13,598621846296300005000876844386

0,8290

Entre 39 et 40°

39,6587315648276904009258333961383

0,289256198

16°

16,1328405121331118923472311358334

0,5

Entre 26 et 27°

26,5650511770779893515721937204533

0,866

Presque 41°

40,8925629074563470010890415264752

1

45°

45°

12,56

Entre 85 et 86 °

85,4478366300075891173256624914393

19

87°

86,9872124958166600548819457850051

57,2900

89°

88,9984275643442281937830467049166

169

Entre 89 et 90°

89,6609756755485497756239006787162

5067

Presque 90°

89,9886923665345948266430392503244

12568

Presque 90°

89,9954411378586751730828079184392

Dans un triangle rectangle si l’on connaît 2 côtés on peut avec « Pythagore » trouver la longueur du troisième coté .

            Avec deux longueurs , on peut aussi  trouver la valeur  d’un sinus ; cosinus ou tangente d’un angle  pour ensuite trouver la valeur en degré de cet angle , et ensuite en déduire la valeur des deux autres angles ….

Rappels :

La somme des angles dans un triangle est de 180° . La somme dans un triangle rectangle est de  180° = 90° + ( somme des 2 angles aigus) .

(ces deux angles aigus ,dont leur somme est de 90°, sont appelés : angles complémentaires)

Dans un triangle rectangle , si je connais la longueur  de deux côtés , j’applique  « Pythagore » pour trouver la longueur du troisième côté.

Dans un triangle rectangle , si je connais la longueur  de deux côtés , j’applique  le sinus , le cosinus ou la tangente  pour trouver la valeur d’un des angles aigus .

i9

IV ) Recherche par calculs d’éléments d’un triangle rectangle.

Voir pour chaque cas :

Info 1  sin ;

Info 2 cos ,

Info 3  tan ;

1 ) Recherche d’un angle connaissant les longueurs de deux côtés.

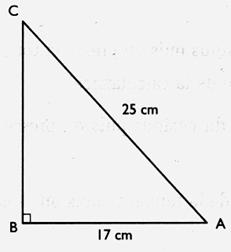
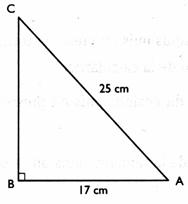
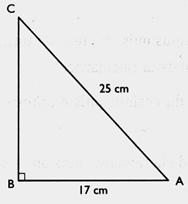
1°) On donne la longueur de l’hypoténuse et la longueur d’un côté  d’un triangle rectangle.

Que représente [CA ] et [BA] pour l’angle A ?.

Que représente [CA ] et [BA] pour l’angle C ?.

Réponse :Pour l’angle A :  le segment  CA  (  [CA] )est l’hypoténuse  , le segment BA  ( [BA]) est le côté adjacent. 

Pour l’angle C : le segment  CA  (  [CA] )est l’hypoténuse  , le segment BA  ( [BA]) est le côté opposé . 

Calculs :

a) On demande de trouver la valeur de l’angle A , en degré .

b) En utilisant les relations trigonométriques trouver la valeur en degré de l’angle C.

Solution :

a)     Calcul de la valeur de l’angle A , en degré .

.

Procédure :

Solution :

1°)inventaire des données :

[CA] est l’hypoténuse , [BA] est le côté adjacent à l’angle A

[CA ] =  25 cm   et  [BA]= 17 cm

2°) Etablissement des formules :

( à partir des 3 définitions) 

Sin A = ;cos A =   ; tan = 

Analyse :La relation trigonométrique  « cosinus »  est la seule  formule utilisable avec les données .,

cos A = 

3°) calcul du  cos A =   

cos A =   ; cos A = 0,680 0

4°) Calculatrice : recherche de la valeur angulaire.

= 47,1563569564036622080449988396549

= 47,16°

(à vérifier sur un dessin à l’échelle )

b)      Calcul de la valeur de l’angle C , en degré .

.

Procédure :

Solution :

1°)inventaire des données :

[CA] est l’hypoténuse , [BA] est le côté adjacent à l’angle A

[CA ] =  25 cm   et  [BA]= 17 cm

2°) Etablissement des formules :

( à partir des 3 définitions) 

Sin C = ;cos C = ; tan C =    

Analyse :La relation trigonométrique  « cosinus »  est la seule  formule utilisable avec les données .,

Sin C =   

3°) calcul du  sin C =   

Sin C =   ; sin C  = 0,680 0

4°) Calculatrice : recherche de la valeur angulaire.

= 42,8436430435963377919550011603451

= 42,84°

(à vérifier sur un dessin à l’échelle )

Remarque : les angles  = 42,84°   et   = 47,16°  ont pour somme :

 42,84°  +  47,16°  = 90,00°  soit 90°

Ce qui vérifie que dans un triangle  la somme des angles est de :

90° + 42,84°  +  47,16° =  180° ;soit   90° + 90° = 180° 

2 )Recherche de la longueur d’un côté  connaissant un angle* et la longueur** d’un autre côté .

Cd :Info plus .

*On connaît  la valeur angulaire de l’angle  A ou  de  l’angle B .

** On connaît soit l’angle en A ou en B , on recherche  la longueur du  côté adjacent ou du côté opposé qui forme l’ angle A ou B .

Exemple 1   :

Objectif : rechercher la longueur du côté opposé à un angle .

     Soit un triangle CBA rectangle en B .

      On donne l’angle A  = 42°  et  [B A]  = 20 cm.

Question : on demande de calculer la longueur du côté [ B C

Procédure :

Solution :

1°)inventaire des données :

 [BA] est le côté adjacent à l’angle A.

On obtient ,avec la calculatrice, la valeur décimale de :

Sin 42° : 0,669 1

Cos 42° : 0,743 1

Tan 42° :  0,9004

[BA ] =  20 cm   et    =  42 °

2°) Etablissement des formules :

( à partir des 3 définitions) 

Sin  = ;cos  = ; tan  =   

Analyse :La relation trigonométrique  « tan »  est la seule  formule utilisable avec les données . Il faut convertir tan 42° en valeur décimale avec la calculatrice . 

tan  =  

tan 42° = 0,900404044297839945120477203885372

3°) calcul de  CB  à partir de l’égalité : tan  =  ;  On remplace les lettres par les valeurs connues .

0,9004 =  

4°) transformation  ( produit en croix)

             =

20  0,9004 =  1  CB

CB = 18,00 cm

Exemple 2 :

Objectif : rechercher  la longueur du côté adjacent à un angle .

on reprend l’ énoncé précédent  on modifie une donnée .

     Soit un triangle CBA rectangle en B .l’angle A  = 42°  et  [C A]  = 30 cm.

Question : on demande de calculer la longueur du côté [ B C] 

Procédure :

Solution :

1°)inventaire des données :

 [CA] est l’hypoténuse du triangle .

On obtient ,avec la calculatrice, la valeur décimale de :

Sin 42° : 0,669 1

Cos 42° : 0,743 1

Tan 42° :  0,9004

[CA ] =  30 cm   et    =  42 °

2°) Etablissement des formules :

( à partir des 3 définitions)  , On cherche  CB .

Sin  = ;cos  = ; tan  =   

Analyse :La relation trigonométrique  « sin »  est la seule  formule utilisable avec les données . ( on connaît deux valeurs sur trois )

Sin  = 

3°) calcul de  CB  à partir de l’égalité : Sin  = ;  On remplace les lettres par les valeurs connues .

0,6691 =  

4°) transformation  ( produit en croix)

             =

30  0,6691 =  1  CB

CB = 20,07cm

VOIR les TRAVAUX FORMATIFS.

Les travaux auto formatifs sont destinés à préparer le devoir formatif .

Le devoir formatif  une fois passé  et validé  permet de passer les travaux certificatifs .( diplôme)

Angle :

Sinus

Cosinus

Tangente

7°

0,12186934340514

0,99254615164132

0,12278456090290

30°

0,5

0,86602540378443

0,57735026918962

84°

0,99452189536827

0,10452846326765

9,51436445422258