Le plus grand coté d’un triangle rectangle s’appelle   : HYPOTHENUSE

Les deux autres cotés  du triangle rectangle forment un angle de 90°

Un coté de l’angle droit et l’hypoténuse forment  un angle dit « aigu ».

Le troisième coté du triangle « empêche » l’ouverture ou la fermeture de l’angle obtenu.

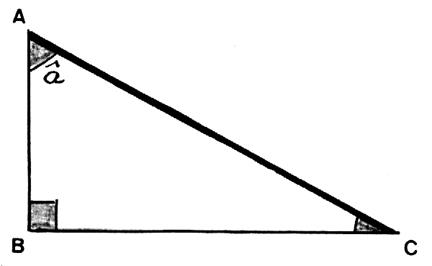
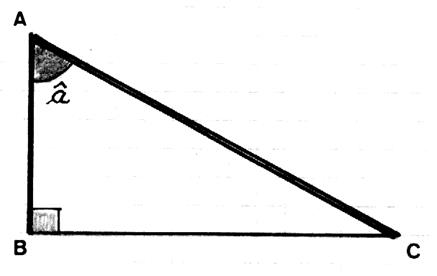
Que peut-on dire du  coté BC : (par rapport à l’angle â) ?

Soit l’angle : â

Le coté BC s’appelle « coté opposé » a l’angle â

(on peut imaginer que l’on tend une corde de  B à C  pour s’opposer  à l’ouverture de l’angle â )

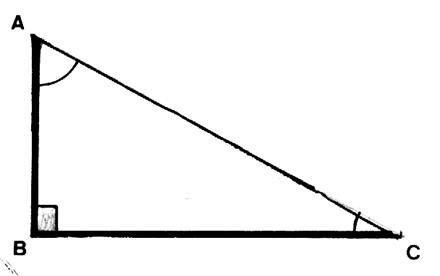
Soit l’angle : â      ( nous nous plaçons en « A »)

Le coté  AB  s’appelle « coté adjacent » à l’angle â

(retenir que le coté adjacent à l’angle et l’hypoténuse forme un  angle , cet angle est dit « complémentaire »)

 Pour former un angle il faut deux coté issus du même sommet :

                      Dans le triangle rectangle ,les angles  aigus  ( dit aussi  « complémentaires » )   sont formés  par deux cotés appelés :   « coté adjacent » et « hypoténuse ».

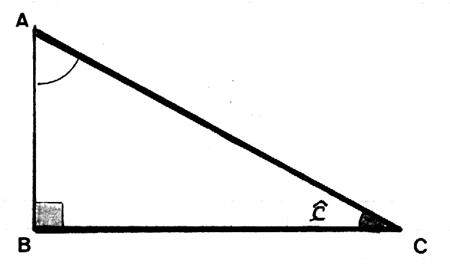
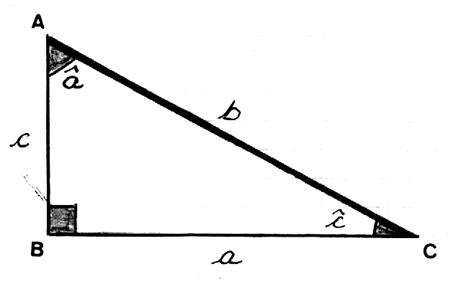
Application : dans  le triangle rectangle :

       l’angle « a » ,de sommet A ,est formé avec son coté adjacent AB et l’hypoténuse AC

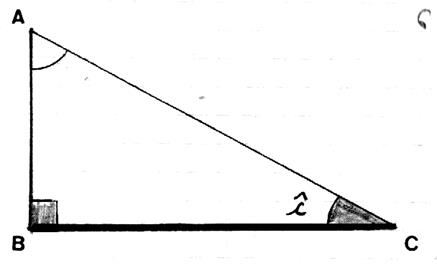
Application : dans  le triangle rectangle :

       l’angle « c » ,de sommet C  ,est formé avec son coté adjacent BC  et l’hypoténuse AC

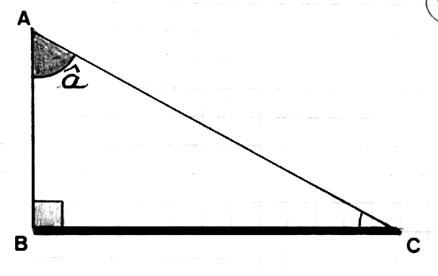
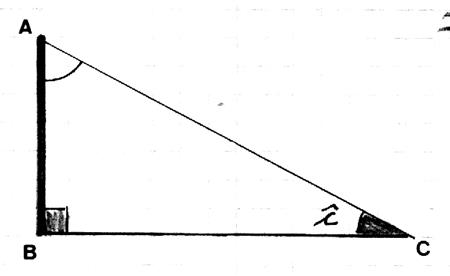
Considérons l’angle 

Soit l’angle    :   le coté BC  s’appelle « coté adjacent » a l’angle 

Remarque : le coté BC est  « opposé » à l’angle « a ».

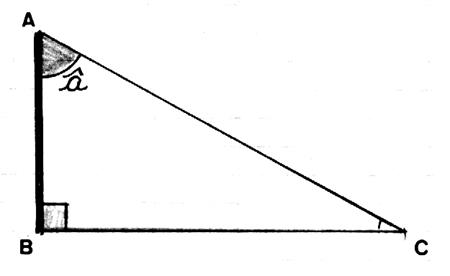
Considérons l’angle 

Soit l’angle    :  le coté AB (ou BA) s’appelle « coté opposé » à l’angle 

Remarque : le coté AB  est  « adjacent  » à l’angle « a ».

Se souvenir qu’ :   un coté  d’un triangle rectangle  est  ,à la fois, le  « coté adjacent » d’un angle  et  le   « coté opposé » de l’autre angle complémentaire.

 Un triangle rectangle ;  c’est trois cotés et 5  noms différents.

Les cotés formant l’angle droit ont deux noms chacun, cela  « en fonction »  , de l’angle considéré.

Soit l’angle : â

Soit l’angle : â

application : dans le triangle rectangle :

     on considère   l’angle « a » .............................................................................................................

Considérons l’angle 

.................................................................................................. :

Considérons l’angle 

.................................................................................

Dites tout ce que l’on peut dire sur la figure ci contre :

Combien de valeurs peut -on mesurer ?

Donner ces mesures..