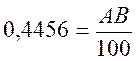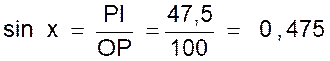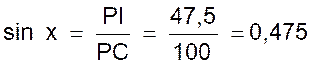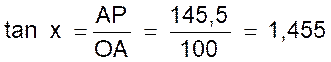|
|
|
|||||||||
|
|
|
|
||||||||
|
|
||||||||||
|
|
|
|||||||||
|
TRIGONOMETRIE :
activités de tracés ou de mesures d’un angle sans rapporteur
. Utilisation
des rapports trigonométriques .Usage des tables ou de la calculatrice. APPLICATIONS : Constructions d’angles connaissant leurs rapports (dit
aussi : lignes) trigonométriques. |
||||||||||
|
Les définitions
des rapports (lignes)
trigonométriques d’un angle
aigu permettent de construire un angle étant donné l’une de ses lignes
trigonométriques. Chapitres : |
||||||||||
|
|
||||||||||
|
|
||||||||||
|
|
||||||||||
|
5°) construction d’un angle connaissant le sinus.
(deux méthodes) |
||||||||||
|
|
||||||||||
|
|
|
|||||||||
|
|
|
|||||||||
|
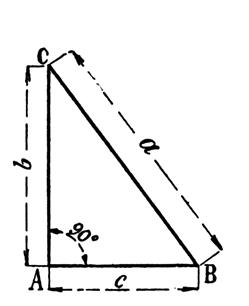
1°) ) tracer un triangle rectangle dont la longueur de l’hypoténuse est égale
à 100 mm. |
||||||||||
|
Activité n°1 :Relevez la valeur des 3 angles avec le rapporteur. Angle droit = ; petit angle
= ; angle moyen = On nommera le petit
angle : « alpha »
symbole « a » On nommera le moyen angle : « bêta » symbole « b » Nommez l’hypoténuse « c. » ; le petit coté « a » ; le coté moyen « b » a) Sur le dessin
relevez la longueur du plus petit côté
« a » : calcul : Divisez la longueur de ce petit coté par
la longueur de l’hypoténuse . ( a : c
»
) Vous trouvez un
nombre inférieur à zéro , ce nombre porte le nom de
« sinus » . Remarque : Si le
« petit angle : a » varie la valeur de ce sinus varie. On dira que le calcul de la longueur du petit coté sur la longueur de
l’hypoténuse est appelé : sinus alpha
que l’on notera : sin a ; à partir de cette valeur on
peut trouver la valeur de l’ angle alpha en
degré soit avec la calculatrice , soit
avec la table des nombres trigonométriques . |
||||||||||
|
|
|
|||||||||
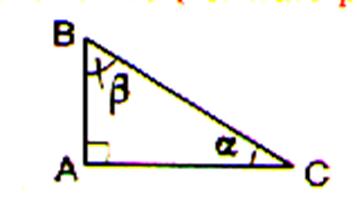
2°) Désignation conventionnelle
: Triangle
rectangle , par convention on désignera
les cotés et les angles comme ci dessous.
|
||||||||||
AB
= c
; opposé à
|
|
|||||||||
|
3°) Comment construire un
angle sans rapporteur , en connaissant un de ses
rapports trigonométriques. :
« sinus » ou « cosinus » |
||||||||||
|
Prendre une
table de nombres trigonométriques ainsi qu’une calculatrice
scientifique : nous allons comparer les résultats ! |
||||||||||
|
Voir : « tracé d’un triangle » |
||||||||||
|
A) Tracer un angle à partir de
la valeur de son sinus : |
||||||||||
|
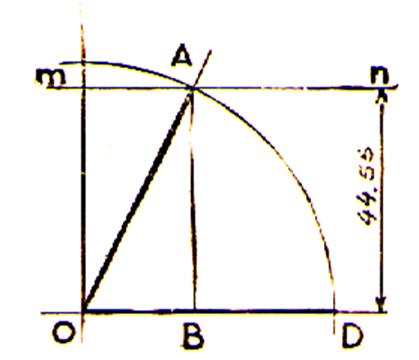
On donne pour L’angle « Procédure :
On trace une droite OA = 100 on sait
on en déduit
que : AB = 44,56 le tracé sera approximatif ! le « sinus |
|
|||||||||
|
B)
Construction d’un angle à
partir du cosinus d’un angle donné : |
||||||||||
|
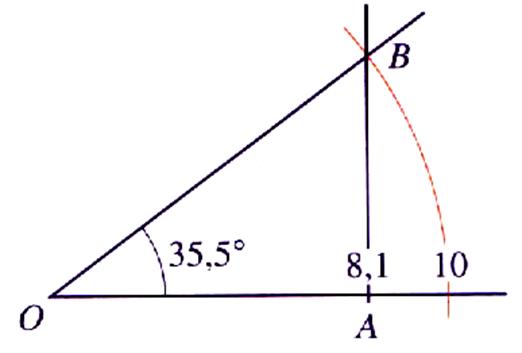
On
recherche le cosinus de 35,5° : » 0,81 soit = Procédure de tracé : -tracer
un arc de rayon 10 cm ; -
sur [ 0x)
placer le point « A » tel que OA = 8,1 cm -
tracer une perpendiculaire à [ 0x) passant par « A » et coupant l’arc de
cercle en « B » -
l’angle AOB vaut 35,5° (à
vérifier avec un rapporteur) |
|
|||||||||
|
Conclusion :pour construire un
angle on peut utiliser un rapport
trigonométrique. |
||||||||||
|
4°)
Comment donner la MESURE d’ un
ANGLE sans rapporteur : en se servant d’un règle graduée et d’une table de
rapport trigonométrique. |
|
|||||||||
|
Ou comment donner la mesure d’un angle « x O
y » donné sans le rapporteur . |
|
|||||||||
|
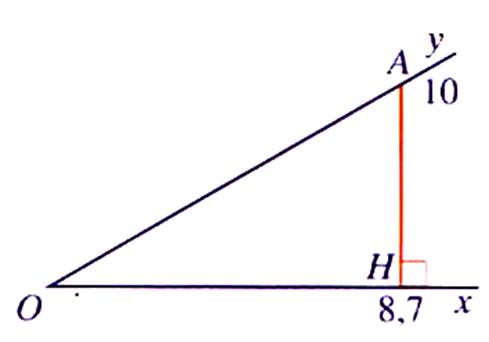
Procédure : - placer un
point « A » sur [O y) tel que OA = 10 cm ; -
tracer la projection
orthogonale de « A » sur
[O x)
(image de « A » est « H ») -
mesurer la longueur « OH » ( = 8,7 cm) -
on en déduit le cosinus de l’angle « xOy » = -
A l’aide de la calculatrice ou
de la table : on obtient la valeur de l’angle = 29,5° |
|
|
||||||||
|
5°)
construction d’un angle connaissant le sinus. (deux méthodes) |
|||
|
a) Construire l’angle aigu
« x » dont le sinus est égal à 0,475. |
|||
|
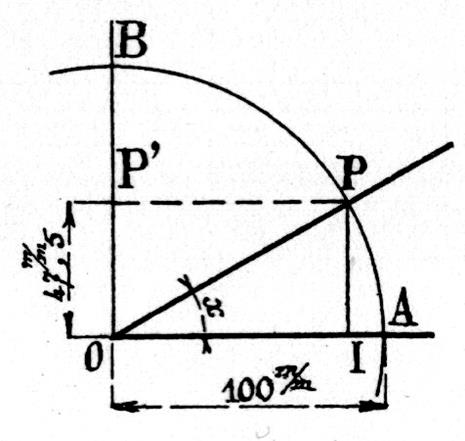
Première méthode : on décrit un cercle de centre o et de rayon unité. ( ci -contre) On prendra par exemple OA = 100
millimètres si l’exercice se fait sur feuille de dessin. Le quadrant OAB étant tracé , on porte sur OB
un segment OP’ = 47,5 mm . La parallèle P’P à OA donne sur le cercle le point
P que l’on joint au point O pour avoir
l’angle « x » demandé car :
|
|
||
|
Nota : « 0,475 » :
en utilisant des tables ou une calculatrice qui donnent les sinus des angles
, on pourra trouver la valeur de cet angle et comparer cette valeur avec
celle que donne la mesure au rapporteur de l’angle construit. |
|||
|
b) Deuxième méthode : |
|||
|
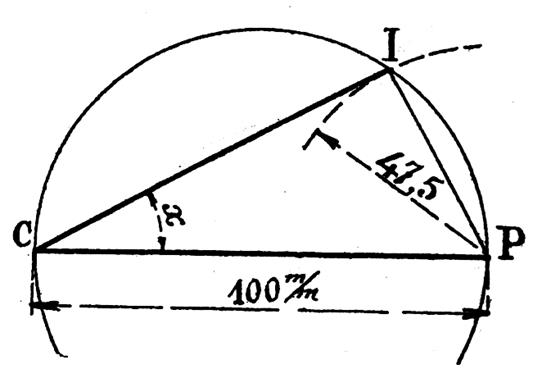
On décrit un cercle de diamètre CP = 100 millimètres (ci contre) et du
point P comme centre avec une ouverture de compas égale à 47,5 mm , on décrit un arc de cercle coupant la circonférence O
au point I ; l’angle cherché n’est autre que l’angle C formé par le diamètre CP et la corde CI car la
figure ci contre donne encore , d’après la
définition du sinus :
|
|
||
|
6°) Construire l’angle |
|||
|
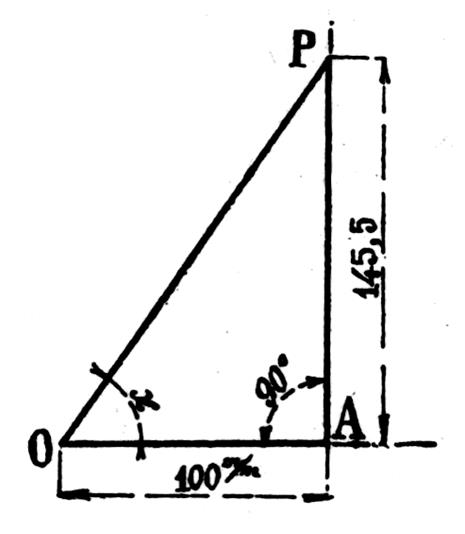
Sur une droite Au point A on élève la perpendiculaire et sur cette perpendiculaire on
porte AP = 145,5 mm . En joignant P au point O on obtient l’angle cherché « x » car
on a bien :
|
|
||