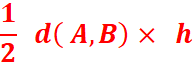DOSSIER :Le théorème de PYTHAGORE

1°) Démontré par Euclide 

2°) Découpage

Pythagore : disciple de Thalès , ce mathématicien et philosophe grec né à Samos ( v. 570- v.480 av. J-C) était réputé pour son éblouissante personnalité .Il effectua de nombreux voyages en Perse , en Gaule , en Crète , en Egypte , avant de fonder à Crotone ( sud de l’Italie) en 540 av. J. -C) une secte ou il enseignait à ses adeptes, outre le culte des nombres , la théorie de  la réincarnation et ….de surprenant principes de diététique. Il nous à légué le « système décimal » , les tables de multiplication et le fameux théorème de Pythagore.

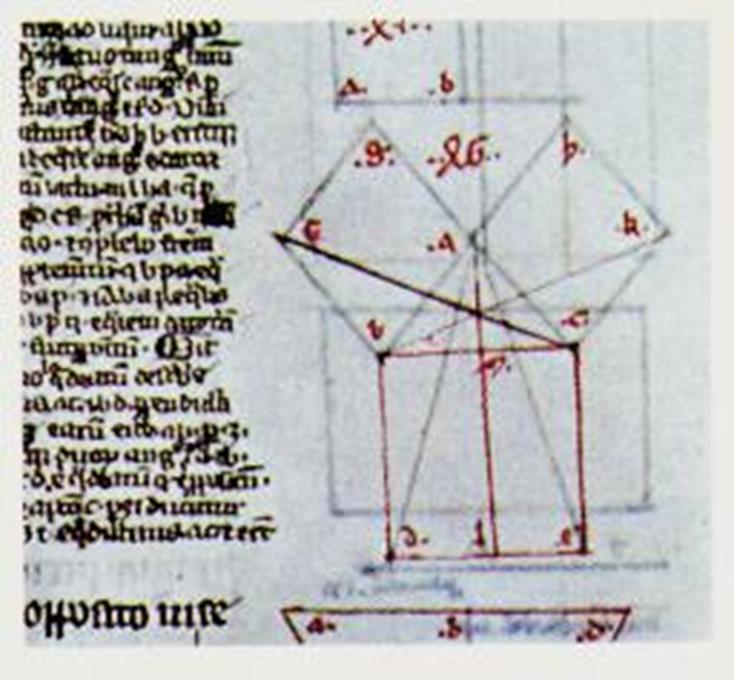
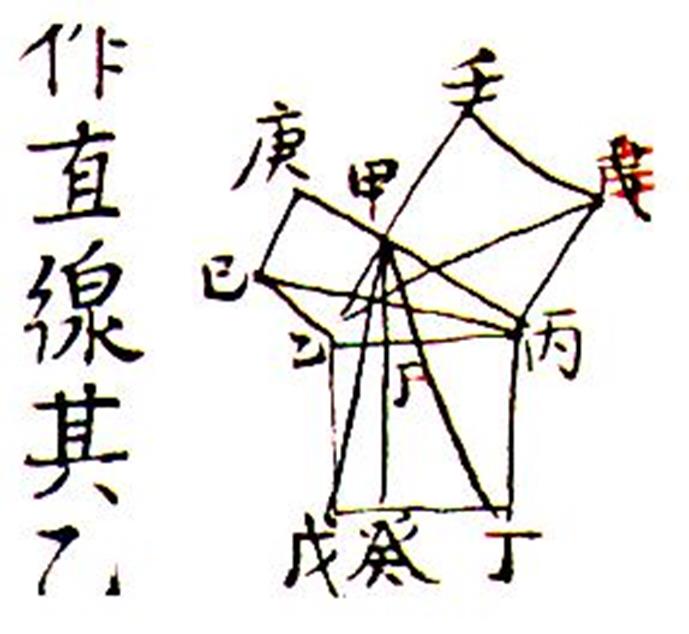
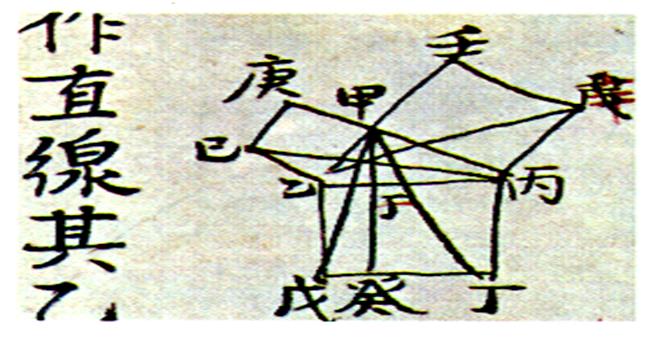
Document ancien :

Document ancien :

COURS :

1°) démontré par Euclide ;

Le théorème de Pythagore affirme :

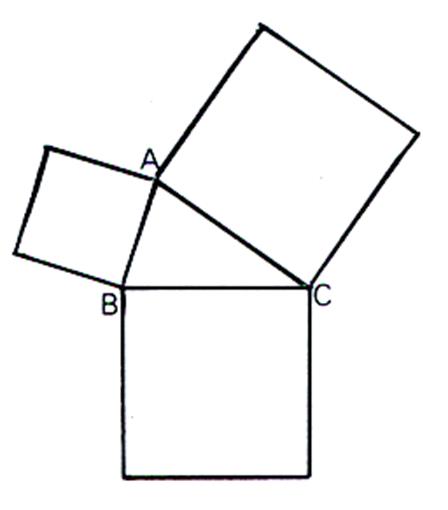
Le théorème de Pythagore affirme que dans un triangle rectangle ,

  ( A,B,C) rectangle en A , les longueurs des côtés AB , BC , AC sont liées par la relation :

BC²  =   AB²  + AC² 

Ce résultat , qui était utilisé de manière empirique par les Babyloniens , aurait été démontré pour la première fois par  Pythagore , au VI^e  siècle avant J.C. L’enseignement du philosophe grec ayant été purement oral , on ne dispose en fait d’aucune preuve de l’existence d’une telle démonstration , à cette époque .

Par contre , on sait que cette preuve figure dans le livre 1 des éléments  d’Euclide , rédigé au III^e siècle avant J.C.

Rappel sur l’aire d’un triangle

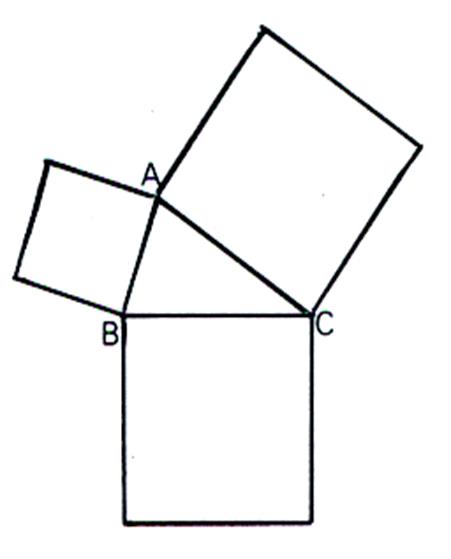
Pour démontrer la propriété précédente  Euclide s’appuie sur le fait que tous les triangles qui ont la même base et la même  hauteur ont la même aire .

INFO +++ : rappel

Ainsi les triangles ( A,C,B) ; ( A,C’,B) , (A ,C’’,B) ont la même aire . Elle est égale à :

Pour démontrer le théorème de Pythagore  , Euclide  démontre que :

Si  l’aire du carré ayant  comme côté l’ hypoténuse  BC est égale à la somme de l’aire du carré de côté AB et l’aire du carré de côté AC : on aura démontré  que    BC²  =   AB²  + AC²

Raisonnement :

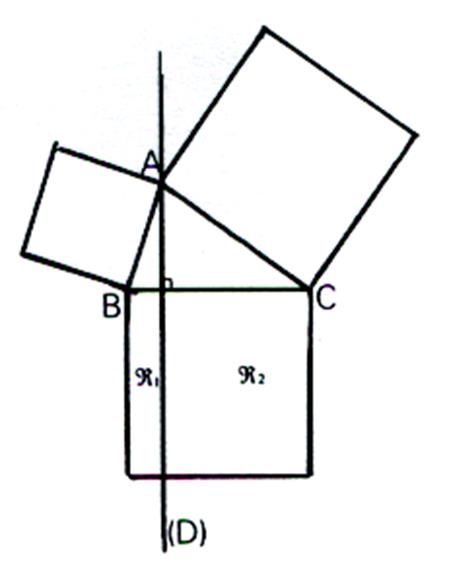
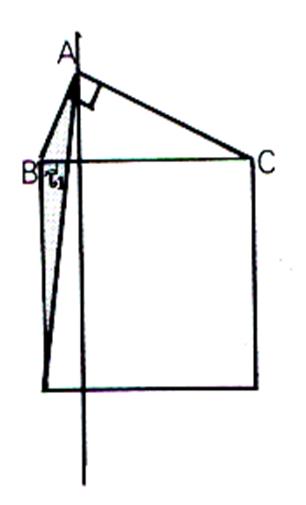
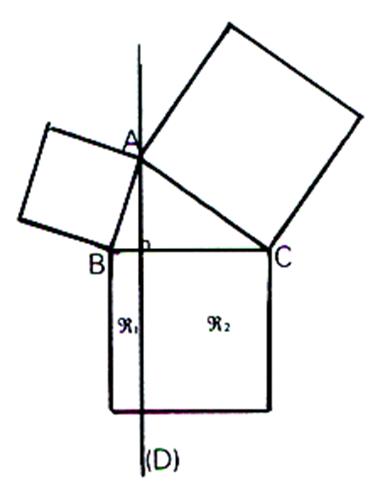
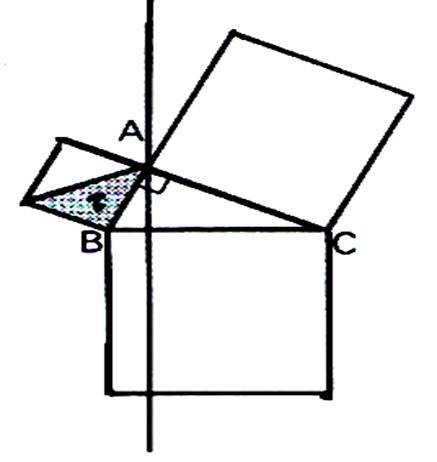
1°) Nous traçons la perpendiculaire ( D) au côté BC passant par A .

Elle coupe le carré de côté BC en deux rectangles notés R₁   et R₂  .

On a BC² =  aire de R₁ + aire de R₂  .

« Euclide » :

Si nous montrons que l’aire de R₁   est   égale à l’aire du carré de côté AB  et que l’aire de R₂  est égale à l’aire du carré de côté AC . Nous aurons démontré le théorème

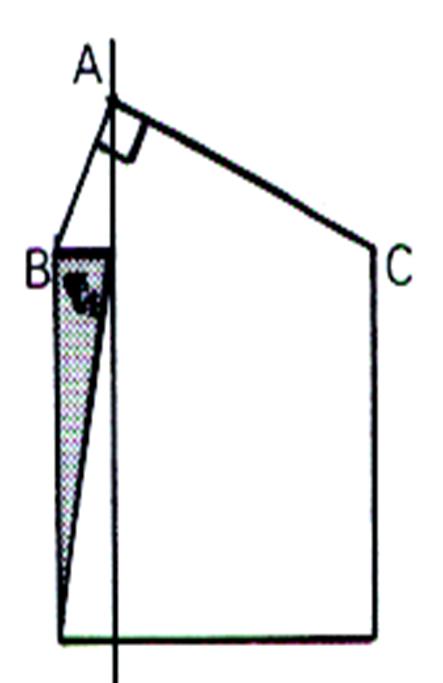
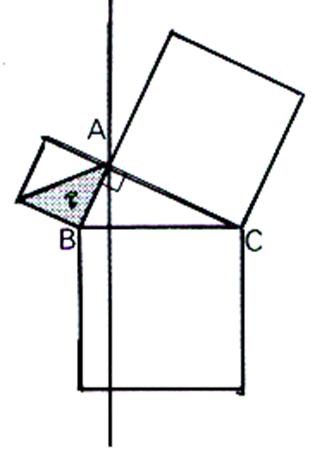
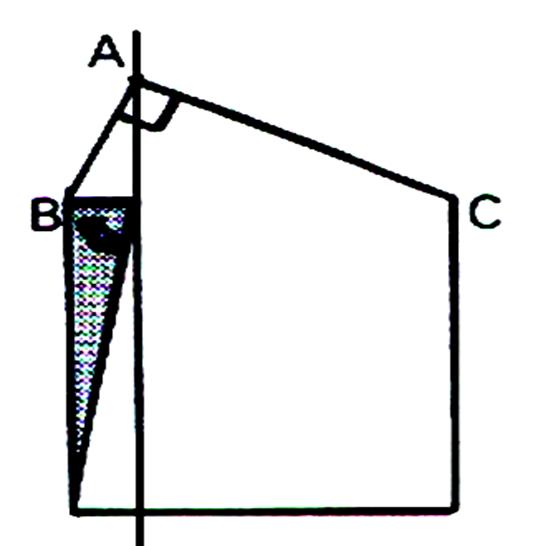
a)    On trace une diagonale  dans le rectangle R ₁  . qui coupe la surface en deux partie égales.

L’aire de R₁  est égale  au double de l’aire du triangle t₁

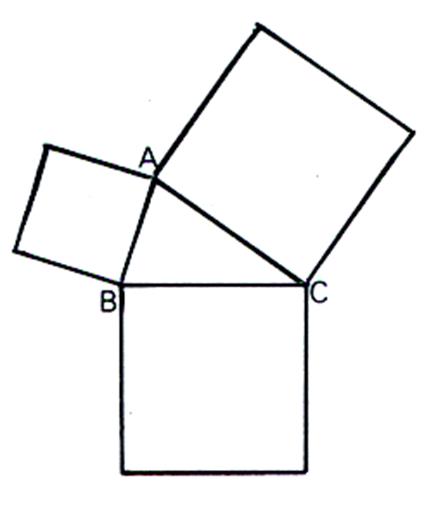
b) Traçons le segment AE ; on obtenons le triangle ( E,B,A) noté  t’₁

Comparons l’aire des deux triangles :

l’aire de ce triangle  t’₁ à la même aire que le triangle  t₁  , car ils ont la même base et la même hauteur_.

Ainsi         t’₁ = t₁

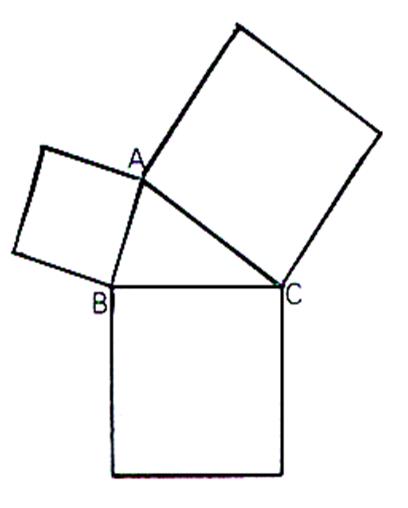
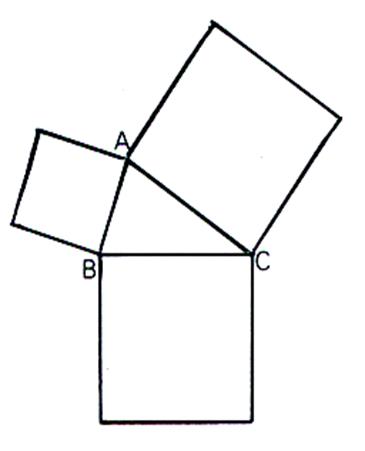
c) Traçons le triangle  (B,F,C) d’aire noté « t » ;

Observons : les  triangles (B,F,C) et (B,A,C) d’aires  t’  et  t’₁ sont superposables par « rotation » autour du point « B » .

 aussi  d(B,E) = d(B,C)  et d(B,F) =d( B,A)

Ils  ont deux côtés égaux de longueurs respectivement égales à AB et BC  et les angles compris entre ces côtés sont égaux .

( voir : triangles isométriques et semblables )

Les triangles  ont donc la même aire :

           t’  ==  t’₁

F

k

d ) Traçons la diagonale  ( A,F ) du carré ( B,F,K,A), on appelle « t » l’aire du triangle  ( B,F,A)

l’aire du triangle  ( F,A,B)  notée « t »  est égale à l’aire du triangle (F,B,C)  notée « t’ » ; car il a la même base et la même hauteur .Cette aire est  égale à

AB²

On a montré que

 en  b)      t’₁ = t₁ 

 en    c)     t’  ==  t’₁ ;

 en   d)     t  ==  t’   =AB²

on peut écrire :

t’₁ =  t’  = t  = t₁  =AB²

On en déduit que l’aire du rectangle noté « R₁ »   est égale à  2 fois l’aire de t₁     soit  =  AB²

De la même façon , on montre que la surface du rectangle  R₂  est égale à  AC^2.

^{Ce qu’il fallait démontrer ! ! ! ! ! ! ! ! ! ! ! !}

2°)Découpage :

Activités permettant de mettre en évidence le théorème de Pythagore :

A )Découper 8 triangles rectangles ayant comme côtés de l’angle droit  , 3 cm et 4 cm .

Mesurer la longueur de l’hypoténuse : ( 5 cm)

B ) Tracer un carré initial de 7 cm par 7 cm .

C 1

C2

Disposer 4 triangles, comme l’indique le pointillé .

Quelle est la surface restante , dans le carré initial ?

 De quelles figures se compose – t – elle ?

Elle se compose de 2 carrés. Calculer les aires de ces carrés .

Faire la somme des aires.

Réponse : ( le carré) ; un carré de 3cm de côté (C₁ aire = 9 cm² )et un carré de 4 cm de côté ( C₂ aire = 16 cm²)  , C₁  + C₂  =  4 + 16 = 25 cm²).

3°) Tracer un  second  carré initial de 7 cm par 7 cm .

Au quatre coin du carré initial disposer les 4 autres triangles rectangles découpés , comme l’indique le pointillé.

Quelle est la figure formée par les 4 hypoténuses ?

Pourquoi ?

Calculer l’aire de C₃ .

Quelle peut-être les conclusions ?

C3

Réponse : (la  figure est  le carré de 5 cm sur 5 cm ; l’aire de C₃  = 25 cm²) ;

En conclusion on remarque que la somme des aires des deux carrés ( C₁  et C₂) formés par les côtés de l’angle droit d’un triangle rectangle est égale à l’aire du carré ( C₃ ) dont la longueur du côté est la longueur de l’hypoténuse .

En résumé : Dans un triangle rectangle , le carré de l’hypoténuse est égal à la somme des carrés des côtés de l’angle droit .

¨Pour le théorème de Pythagore  , on démontre  , comme Euclide que :

A partir d’un triangle rectangle ,  l’aire du carré ayant  comme côté l ’ hypoténuse  BC est égale à la somme de l’aire du carré de côté AB et l’aire du carré de côté AC :

on peut écrire   que

       BC²  =   AB²  + AC²

De cette égalité  en découle des calculs :

Exemple : si on en déduit que  :

CONTROLE