Pré requis :
|
Fractions
équivalentes |
|
Objectif précédent : |
DOSSIER:
LES PROPORTIONS
et
LES GRANDEURS PROPORTIONNELLES :
Vocabulaire et définitions .
|
|
|
|
I
)
Rapport : |
¥ |
|
II
) Rapports égaux : |
¥ |
|
II
) Suite de rapports égaux : |
¥ |
|
III
) Suites de nombres proportionnelles : |
¥ |
|
IV
) COEFFICIENT DE PROPORTIONNALITE : |
¥ |
|
V
) APPLICATIONS AUX GRANDEURS PROPORTIONNELLES. |
¥ |
|
VI ) PROPORTION : |
¥ |
|
VII
) QUATRIEME PROPORTIONNELLE : |
¥ |
|
COURS |
I ) Rapport :
On appelle « rapport » est le quotient obtenu
par la division d’un nombre par un autre nombre.
Le modèle mathématique d’un « rapport » est « une
écriture fractionnaire fraction ».
* en arithmétique le rapport de
deux grandeurs ,la
mesure de la première grandeur lorsqu’on prend la seconde pour unité , ou
encore quotient du nombre qui mesure la
première par le nombre qui mesure la seconde avec la même unité ..
II ) Rapports
égaux :
On appelle « rapports égaux » des
divisions qui ont le même quotient et dont
le reste des divisions est nul .
- Le modèle mathématique de deux rapports égaux est l’égalité de deux
fractions.
- Traduction en langage mathématique : 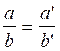
II ) Suite de
rapports égaux :
Lorsque nous avons plus de deux
rapports égaux nous pouvons dire
que nous avons une « suite de
rapports égaux » , le quotient de chaque rapport
étant identique , c’est un nombre dit « constant » appelé « k ».
-
Traduction en langage mathématique :
-
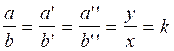
III ) Suites de
nombres proportionnelles :
Deux suites de nombres « S1 » = { ( y1 ;
y2 ;y3 ; ....)} et « S2 »
»= {(
x1 ;x2 ;x3x ;......)}
forment une suite « Sproport. »
de nombres proportionnels si elles forment une suite de rapports égaux .
important : remarquer que la première suite contient
les éléments « y », par convention.
Traduction mathématique :
Sproport.
= ![]() si
si ![]() =
=![]() =
=![]() =.........
=.........
IV
COEFFICIENT DE PROPORTIONNALITE :
Nous pouvons constater que les rapports d’un nombre (y
) ,de la première suite, sur le nombre ( x ) de la deuxième suite ,de même rang (exemples
![]() ou
ou ![]() ... ) .donne un même
nombre ,on dit que le « rapport » est constant . (voir « rapport égaux » )
... ) .donne un même
nombre ,on dit que le « rapport » est constant . (voir « rapport égaux » )
ce nombre s’appelle
« coefficient de proportionnalité».
On appelle « coefficient de proportionnalité » le nombre
constant représentant la valeur commune de tous les rapports de deux suites de
nombres qui forment une suite de nombres proportionnels.
Le coefficient se notera
toujours par la lettre « k ».
V )
APPLICATIONS AUX GRANDEURS PROPORTIONNELLES.
Sciences :
Définition
de « grandeur » :on appelle « grandeur » un nombre associé à une
unité de mesure.
Lorsque deux grandeurs de nature
différentes : ( exemples un prix en fonction de
la masse soit des mesures en kg et €
); si elles varient en même temps dans un même rapport (exemple 10
francs pour un kilogramme , noté : 10 € .kg-1 ) ,on dira que
nous avons des grandeurs proportionnelles.
VI
)
PROPORTION :
On appelle « proportion » l’égalité se deux rapports.
Modèle
mathématique :
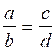
VII ) QUATRIEME
PROPORTIONNELLE :
Remarque :
Lorsque l’on connaît 3 valeurs sur 4 ,dans une
proportion, on peut trouver la « quatrième » valeur . On dira «
rechercher la quatrième proportionnelle. »
Procédure :faire le produit
en croix
,faire le calcul avec les deux nombres ;diviser les deux membres de
l’égalité par le nombre multiplicateur de « x »
Exemple : trouver la valeur de « x » dans
:
![]() =
= ![]() « x »
est la quatrième proportionnelle .
« x »
est la quatrième proportionnelle .
Résolution : 7,5 x = 15
fois 2,3 :
7,5 x
divisé par 7,5 = 15 multiplié par 2,3 divisé par 7,5
|
|