Auteur : WARME R.

 

MATHEMATIQUES :Niveau V.

 

 

 

 

 

 

 

DOSSIER n° 25 / 25

 

DOCUMENT « ELEVE»

 

 

 

LES CARRES:

 

 

Les opérations simples

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

NOM : ………………………………

Prénom : …………………………..

 

Classe :…………………..

 

Année    scolaire : ………………………                                        

 

Dossier pris le : ……/………/………

 

Validation de la  formation :    O -  N

           

 Le : ……………………………………..

Nom du  formateur  : ……………………

 

ETABLISSEMENT : …………………………………………..

 

 

 

DOC. INFO : Professeur - Formateur

25 / 26

DOC : livre  Elève .Cours  interactifs - et travaux +  corrigés.

TITRE :   «  Carrés » d ' opérations simples .Leçon  4/5  .

 

DOSSIER  N°25

COURS  INTERACTIF

«  Carrés » d ' opérations simples .Leçon  4/5  .

Information « TRAVAUX »

Cliquer sur  le mot !.

INFORMATIONS PEDAGOGIQUES :

NIVEAU :

Formation  Niveau V  (inclus le CAP et CFA)

Objectif :  n° 4/5 sur les carrés

OBJECTIFS :

=savoir  calculer les carrés d’opérations simples.

Prépare les Identités Remarquables , utilisées pour résoudre les équations du second degré .

I ) Pré requis:

 

puissance d' un nombre

3D Diamond

II ) ENVIRONNEMENT du dossier :

Index         Filescrosoft Officeverte

Objectif précédent :

1°)   Sphère metallique

2°) le « carré » d’un nombre.

3°) Les I R  déjà vu : cours N°7

 

Objectif suivant :Boule verte

1°) Encadrement

2°) généralités sur les Puissances d’opérations simples

3°) les racines carrées d’opérations simples

Vu : les Identités remarquables ( carrés d’une somme ; carrée d’une différence)

voir : les IR et le calcul mental

1°) Tableau       Sphère metallique    75a

2°) tableau

3°) liste des cours.

Sciences          Sphère metallique

III )  LECON  n° 25  «  Carrés » d ' opérations simples .

CHAPITRES :

I ) CARRE d’une somme :  ( voir : calcul mental )

II ) CARRE d’une différence : (voir : calcul mental )

III )  CARRE d’un  produit  : ( a  b )2

IV )  CARRE  d’un quotient ; d’une division ( fraction)  : ( a : b )2  ou ( a / b )2  ou ()2

V  ) puissance au carré

IV)   INFORMATIONS  «  formation leçon » :

Test

 Boule verte

COURS  Boule verte

Travaux  auto - formation.

 

Corrigé des travaux  auto - formation.

Contrôle Boule verte

évaluation Boule verte

Interdisciplinarité.             Boule verte

Corrigé Contrôle

Corrigé évaluation

Info plus  sur les puissances et racines Nièmes

V )   DEVOIRS  ( écrits): Boule verte

 Devoir diagnostique L tests.

 Devoir  Auto  - formatif  ( intégré au cours)

  Devoir Formatif  « Contrôle : savoir » ;   ( remédiation)

 Devoir  Formatif  «  Evaluation   savoir faire »  ( remédiation)

Devoir sommatif .

Devoir certificatif : ( remédiation )

* remédiation : ces documents peuvent être réutilisés ( tout ou partie) pour conclure une formation .

 

 

 

 

 

 

 

Leçon

Titre

N°25

LES  PUISSANCES  « CARREES » d ' opérations simples

CHAPITRES

 

I ) CARRE d’une somme :  voir : calcul mental

II ) CARRE d’une différence : voir : calcul mental

III )  CARRE d’un  produit  : ( a  b )2

IV )  CARRE  d’un quotient ; d’une division ( fraction)  : ( a : b )2  ou ( a / b )2  ou ()2

V  ) puissance au carré

 

 

 

 

COURS

 

 

Dans les exercices suivants ,nous prenons le cas où les  deux nombres différents « a » et « b » :

 

I ) CARRE d’une somme :  voir : calcul mental

 

                ( a + b ) (a + b)   qui s’écrit   aussi  ( a + b ) 2 

 

le développement de  ( a + b )2   est égal à    a2  + 2ab + b2  

SOS COURS

 

Application numérique :

Si (a ;b)

 

    (a + b )2

a2  + 2ab + b2

conclusion

( 2 ;3)

(2 + 3 )2 =    25

22  + 223 + 32   =

4    + 12         + 9   =  25

(a + b )2 = a2 + 2ab + b2

Forme algébrique :

 

( x ; y )

 

(x + y )2

x2  + 2xy + y2

(x + y )2 = x2+ 2xy + y2

 

Autres applications :

Application numérique

a)  Calcul de ( 30 + 2 )2

On pose :   ( 30 + 2 )2   = 302  + 2 fois 30 fois 2  + 22

calculs intermédiaires :

302  = 900 ; 2 fois 30 fois 2 = 120 ; 22   = 4

( 30 + 2 )2   = 900  +  120  + 4

calculs intermédiaires :

900 + 120 + 4  = 1024

( 30 + 2 )2   = 1024

Application algébrique :

b)   ( x +1 ) ( x + 1 )  qui s’écrit        ( x + 1 ) 2 = x2  + 2x + 4

 

c)   ( 3x + 2 ) ( 3x + 2 ) qui s’écrit   ( 3x + 2 ) 2  =  9x2  + 12x + 4

 

II ) CARRE d’une différence : voir : calcul mental

 

 

 ( a - b ) ( a - b ) qui s’écrit   aussi   ( a - b) 2 

le développement de ( a - b) 2  est égal à   a2 –  2ab +  b2 

SOS COURS

 

Application numérique :

 

Si (a ;b)

(a - b )2

a2  - 2ab + b2

conclusion

( 5 ;2)

(5 –2  )2 = 32 =

9

52  -  252 + 22=

25 – 20  + 4 =  9

(a - b )2 = a2 - 2ab + b2

Forme algébrique :

( x ;y)

(x - y )2

x2  - 2xy + y2

(x + y )2 = x2- 2xy + y2

 

A )  Application calcul : ( 30 - 1 )2

 

On pose :   ( 30 - 1 )2   = 302  - 2 fois 30 fois 1  + 12

calculs intermédiaires :

302  = 900 ; 2 fois 30 fois 1 = 60 ; 12   =  1

( 30 + 2 )2   = 900  - 60  + 1

calculs intermédiaires :

900 - 60 + 1  = 940 + 1  = 941

( 30 -  2 )2   = 941

 

B ) Application « algèbre »

 

Exemples :  

 

a)  ( x -1 ) ( x - 1 )  qui s’écrit   ( x - 1 ) 2 = x2 –2x + 1

 b)  ( 3x - 2 ) ( 3x - 2 ) qui s’écrit   ( 3x - 2 ) 2   =  9 x2  - 12x + 4

 

 

III )  CARRE d’un  produit  : ( a  b )2

 

A retenir :  ( a  b )2     =   a 2 b2

 

a ; b

( a  b )2

a 2 b2

conclusion

2 ; 3

( 2  3)2   = ( 6 ) 2 = 36

2 2 32  = 4 9  = 36

( a  b )2  = a 2 b2

2,5 ; 3,2

( 2,5  3,2 )2 =

2,5 2 3,22 =

 

x ; y

( x  y )2  =  (xy)2

x 2 y2

( x  y )2   =   x 2 y2

 

Applications numériques :

( 5  10 ) 2  =

( 5  102 ) 2  =

( 3  10 4) 2  =

 

 

 

 

 

I V )  CARRE  d’un quotient ; d’une division ( fraction) :  ( a : b )2  ou ( a / b )2  ou ()2

 

 

Exemples types :

 

Soit

« a » et « b »

 =  

 =

 

Conclusion :

3 ; 2

()2  = ( 1,5 ) 2 = 2,25

=   = 2,25

 =

 

2,5 ; 3,2

A vous de faire ! !

 

 

x ; y

 

 

 =

 

Applications  Numériques :

 

 =     = 0,49

 

Remarques :

 

Ecriture de puissances : puissances négatives

1°)     peut s’écrire   b-2     ;  

Exemples :  peut s’écrire   2-2   ;      peut s’écrire   10-2

2° )     peut s’écrire  = a b-2 ;   peut s’écrire  = 2 10-2 ;   par extension      peut s’écrire  = 8 10 -2 

3°)      peut s’écrire   : a2 b-2 ;   peut s’écrire   : 22 10-2

Cas particuliers :

A )    = =    = 0,49   ou  4910-2

 

 

 

 

 

 

 

 

 

V )  CARRE d’une puissance : ( a n )2

 

 

« a » et « n »

( a n )2

a 2n

Conclusion :

2 ; 3

( 2 3 )2  = 82 ; (= 64)

2 32  =2 6  =   64

( a n )2= a 2n

2,5 ; 3

( 2,5 3  )2  = 244,14062

 

 

x ; y

( x y )2  =  x 2y

 

 

 

a )   (10-3 ) 2  =   10-6

b)    (10-2 ) 2  =   10-4

c)      ( 81) 2  =  ( 82  )

d)      ( 23) 2  =   ( 26 ) 

Pour les exercices suivants voir la puissance d’une puissance

e )   ( 8  10-3 ) 2  =  ( 82  10-6 )   =  64 10-6

f )  ( 23  10-2 ) 2  =   ( 26  10-4 )  =   64 10-4

 

 

Leçon

TRAVAUX d ’ AUTO - FORMATION sur

N°25

LES  PUISSANCES  « CARREES » d ' opérations simples

 

TRAVAUX  N° 25   d ’ AUTO - FORMATION : CONTROLE:

 

I°) Transformer les égalités suivantes : 

( a + b )²  =

 

 

 

( a – b  )2  =

 

 

 

( a2 )2  =

 

 

 

( an )2  =

 

 

 

 

 

 =

 

 

  =

 

 

 

  =

 

 

 

b-2 =

 

 

 

a b-2     =

 

 

 

a2 b-2    =

 

 

 

  =

 

 

 

TRAVAUX N°25    d ‘ AUTO - FORMATION    EVALUATION :

 

1°)  en utilisant les relations des  IR  , transformer et calculer :

( 30 + 2 )2  =  

( 90 + 3 )2  =  

( 30 – 1 )2  =  

( 90 –3 )2  =  

 

2°) en utilisant  la relation    (an)2 ; transformer et calculer :

( 102 )2  =  

( 103 )2  =  

 

 3°) en vous aidant des  relations suivantes

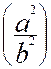 =          ;    =   b-2 ;        = a b-2  et     = a2 b-2 ;

 

4°)  transformer et calculer :

   =

  =

   =  

  =  

 

 

INTERDISCIPLINARITE

 

 

 

VOIR FICHE UTILISATION DE LA CALCULATRICE

 

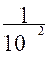idi-font-size:10.0pt; font-family:Arial'>VOIR FICHE UTILISATION DE LA CALCULATRICE