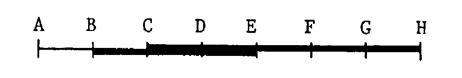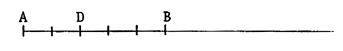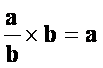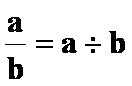CORRIGE DU COURS :  LES FRACTIONS.  (première leçon vue au collège )

I ° )  Fractions ( découvertes) : Exemples de fractions

2°)  Multiplication par une fraction

·        Dont :  Priorité : multiplication et division ..

3°)  Quotient de deux entiers.

4°)  Fractions décimales.

5°)  Fractions représentant le même nombre.

                  I )  Fractions égales dite « équivalentes »

               II ) Simplification de fraction.

COURS.

Info @

I )  Exemple de fractions

Info ++

Exemple 1 : Vous savez que dans une heure il y a 60 minutes.

1 heure égale deux fois 30 minutes . On écrit 1 h = ..2..x 30 min.

inversement  30 minutes égale une ..demi..heure . On écrit  30 min =  h.

et  l’écriture  «  » est une fraction.

Exemple 2 :

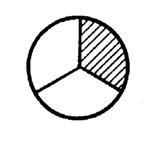
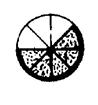
Voici une tarte partagée en 3 morceaux « identiques ».

La partie hachurée correspond à un  « tiers  ….»  de la tarte.

La fraction correspondante  s’écrit : ……...

 Réponse :

Exemple 3 :

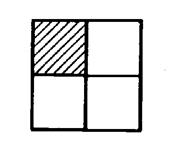
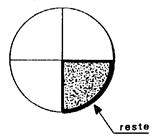
Le carré ci contre a été partagé en 4 carrés de même dimension.

La partie hachurée  correspond à un  « quart »  du grand carré.

La fraction correspondante s’écrit ……

Exemple 4 :

On vous donne un segment [ A H ]  qui a été partagé en 7 segments de même longueur « L »  

 On écrit :  A H = 7 L

Inversement , on dit que « L » représente un septième de AH  et ……………………………….

on écrit : L =  AH

«  » se lit « un sur sept » ( ce qui rappelle que l’on a pris un segment sur les sept.)

Exemple 5 :

Considérons  le segment [ A D ] , on peut dire que «  AD = …. L.

Pour exprimer « AD » à l’aide de « AH » , on considère que l’on a :

partagé  [ A H ] en …. Segment de même longueur  L .

et  pris ….. de ces segments .

On écrit   alors

AD =  AH

«  »  se lit  « trois septièmes »   ou « Trois sur sept »

Activité série 1:  Complétez

AF = ….. AH

DF = ………BG

AD = ….DH

DH = ….AH

EG = ….. AH

CF = ……. CH

AC = …. EH

GC = …….AF

Vocabulaire :

Considérons la fraction 

« 5 » est le numérateur

« 7 » est le dénominateur.

« 5 » et « 7 » sont appelés  les termes de la fraction

Activités série 2: 

On vous donne un segment de droite [ K L ] ci-dessous :

[ K L ] est partagé  en 12 segments de même longueur.

1°) Placez « M » entre « K » et « L » tel que   KM =   KL

2°) Placez « N » entre « K » et « L » tel que   KN =   KL

3°)  Placez «P » entre « K » et « L » tel que   PL =   KL

Activité  série 3: 

Une année  (non bissextile)  correspond à 365 jours. Quelle fraction de l’année représente :

   1 jour   : ………………( ) ………………

Une semaine : ………………( ) ……………………….

Le mois de mai : ……………( ) ………… ;

Exemple 6 :

Reprenons  le segment   [ A H  ] partagé en 7 segments de même longueur « L »

On nous demande d’exprimer « CH » à l’aide de « BE » .

Pour cela , on considère que l’on a :

partagé « BE » en  …  3……. Segments de même longueur « L ».

et pris   «  … 5… » segments de même longueur « L ».

Puisque    ; on écrit alors :     ;  et           se  lit  « cinq tiers »    ou  « cinq sur trois »

Activité   : On vous demande de compléter les égalités suivantes.

BG = ………..     EG

AH = ………………………BE

BF = …………………….BE

DG = ……………BD

BH = …………………..CH

AF = ……………………..CG

Activité   :

On vous donne une droite graduée : [ R S ]   est partagé  en « 6 » segments de même longueur.

On vous demande de placer « T » tel que    et « W »  tel que :

Activité   :

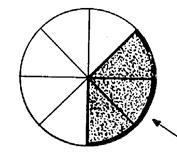
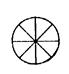
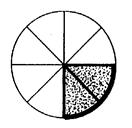
On demande de partager des tartes en 8 morceaux  « identiques »

Chaque morceau représente un … « huitième »  ……de tarte.

La fraction correspondante s’écrit : … «  » ……

1°)  « 5 » personnes prennent chacune un morceau.

Au total  , elles ont pris …les cinq …   huitièmes de la tarte.

        reste

2°) « 8 » personnes prennent chacune un morceau.

Au total, elles ont pris ….8…..huitièmes de tarte. C'est-à-dire …1..tarte..  . La fraction correspondante  s’écrit :…… « »…….

3°) « 11 » personnes prennent chacune un morceau.

Au total, elles on pris …..onze……huitièmes de tarte.

La fraction correspondante  s’écrit :…… « »…….

+

Activité   :

Un commerçant achète un objet qui avec les taxes lui revient à 15 € .

Il le  revend  19 € . Quel est son bénéfice ? ………………………19 – 15 = 4   ....

Quelle fraction  du prix de vente représente  

Le prix d’achat ?  ………………..

15 / 19

Le bénéfice ? ……………………

4 / 19

Quelle fraction  du prix d’ achat représente   ……

Le prix de vente  ?  ………………..

19  / 15

Le bénéfice ? ……………………

4 / 15

II  )  Multiplication par une fraction    ( info ++ la multiplication et la fraction +)

Activités .. :  On vous donne une droite et sur cette droite on a placé deux points « A » et « B ».

Répondre aux questions suivantes :

1°) On vous demande de placer sur cette droite un point « C » , tel que « AC = 4 AB »

indice :  Pour cela , partant de « A3 , vous reporter …4 …fois la longueur AB.

2°) Mesurer la longueur AB =  ( 35 ) ..mm , Calculez la mesure de la longueur de [ A C ].

La longueur « AC » est …….. fois la longueur « AB ».

On dit « 4 fois 35 égale ……………. » et on écrit  «  4 x 35 = ………………..AC   =  ………………………

3°) Vous allez placer sur la droite , entre « A »   et «  B »  , un point « D » tel que       

Pour cela , vous divisez le segment  [ A B ]   en …… segments de même longueur, ( ce qui est déjà fait ) puis vous en prenez ……..à partir de « A »..

4°) Calculez la mesure de la longueur de  [ A D ]   ( unité le mm.)

La longueur « AD » est les ……….de la longueur « AB ».

Pour faire le calcul, vous procédez comme pour la construction.

Vous commencez par diviser par « 35 » par…………………..puis vous multipliez le  résultat par ……

35

Divise par

Multiplie par

Multiplie par 

On dit «  de 35   égale  …….. »  et  on écrit  «  x 35   =  …14.. » ;     « AD = ……….. »

Proposition de solution :   «  x 35   =    ( 35   : 5  ) x 2  =   7  x 2  = …14.. » ;

Plus tard on verra la solution passe par la multiplication de deux fractions :   =…….

A retenir :

Dans la multiplication d’un nombre par une fraction, le numérateur agit comme un opérateur de  « multiplication »et le dénominateur comme un opérateur de « division »

Puisque le dénominateur  est un opérateur de division , le numérateur est un opérateur  de ………..multiplication….

A retenir :

Dans toute fraction le dénominateur est différent de «  zéro » …

Remarque : A la question « 2 », on a calculé «  4 fois 35 » . A la question « 4 », on a calculé  «  x 35 » . « 4 » et  «  » sont des opérateurs.

·        « 4 » est un opérateur entier  ,  «  »  est un opérateur fractionnaire.

·        Dans le cas de l’opérateur entier, on a utilisé  le mot « fois ».

·        Dans le cas de l’opérateur fractionnaire , on a utilisé le mot « de ».

·        Mais dans chacun des cas, « fois » et « de » correspondent à des « multiplications ».

Attention :

Dans le cas d’un produit où l’un quelconque des facteurs n’est pas apparemment un opérateur , évitez d’employer le mot « fois ».

Exemple :  5 x 7 :  dites  «  5 multiplié par « 7 » »  et non pas «  5 fois 7 »

De toute façon, si «  5 fois 7 »  peut se justifier ,   mais  « 0,4 fois 6,8 » n’a aucune  signification et il faut dire impérativement «  0,4  multiplié par 6,8 »

Activité  n° …. :   calculez :

  de  21

  x 21  =  ( 21  :    …. .. )  x  ………..=     …………….x ………………= …………..

  de  36

  x  36  =  ( ……. : ……)  x  ………..=     …………….x ………………= …………..

  de  30

  x  30  =     ………………………………………………= ………………………= …………..

Activité  n° …. :   Vous savez que «  1 h =   60 min. )  Complétez le tableau ci-dessous.

Fraction d’heure.

Valeur en minute.

Activité  n° …. :  

On partage la somme de 3 500 €  entre deux personnes.

La première reçoit les    de la somme ; la   deuxième  reçoit les  de la somme.

Calculez la part de chacune de ces personnes.

Part de la première ( en € ) :    x …….=    ( …….. : …….) x …….=

Part de la deuxième ( en € ):     x …….=    ( …….. : …….) x …….=

En conclusion : La première a reçu ……………………€   ; La deuxième  a reçu ………..€

3°) Priorité : multiplication et division ..           ( voir les priorités dans les calculs …)

Cette partie de cours n’a d’intérêt que pour montrer qu’il n’y a pas de priorité « évidente » entre faire la division et la multiplication ou faire la multiplication et la division… il faut tester et rechercher le quotient exact si il peut exister….

Ordre dans lequel on applique les opérateurs « multiplicateur » « diviseur ».

Activité  n° …. :  

Reprenons le segment [ A B ] du début  du paragraphe et le point « D » tel que «  AD =  AB »

·        Possibilité 1 :  on  divise par « 5 » puis on multiplie  par « 2 ».

Ci contre :  Pour placer le point « D » , on a partagé le segment AB  en ..5… segments de même longueur  ( on a diviser par « 5 »)  et on a pris 2 segments à partir de « A ».(on a multiplié par « 2 »)

·        Possibilité 2 :  Intervertissons les opérateurs : On multiplie par « 2 » puis on divise par « 5 ».

On reporte….. « 2 »…. fois  la longueur « AB » à partir de « A » , on obtient le point « E ».

Puis on partage le segment « AE » en   …. « 5 » …  segments de même longueur.  ( voir comment  diviser un segment graphiquement .@ .)

Placez le point « D » . Vous constatez qu’il est au même endroit  que précédemment. !!

Activité  … :   Calculer  de 15  de deux façons.     ( info plus : multiplication d’une fraction par un nombre)

15

Divisé par « 3 »

5

Multiplié par « 4 »

=

20

C'est-à-dire :   ( 15 :  3  )  x   4  =   20

15

Multiplié par « 4 »

60

Divisé par « 3 »

=

20

C'est-à-dire :   ( 15 x 4   ) : 3  =   20

Vous constatez que l’on trouve le même résultat dans les deux cas ..

Vous prouverez , plus tard qu’il en est toujours ainsi avec d’autres nombres (quand les calculs sont possibles)

Vous admettrez donc : 

A retenir :

Dans la multiplication par une fraction, on peut , ( si le calcul est possible ) intervertir l’ordre des opérateurs de multiplication et de division.

Activité  … :   Après avoir essayé de calculer    de 28  de deux façons différentes , dites en l’expliquant, quelle est la méthode qu’il est préférable d’utiliser  dans ce cas.

( solution : 3 fois 28   le produit diviser par 12 = 7)

3°)  Quotient de deux entiers.      ( info  : le quotient de deux entiers)

Activité … :      

          Calculez  les  x 4    .

x 4   =   ( 4 : 4 ) x 9     =   1 x 9   = 9

De même Calculez  les  x 7    .

x 7    =  (  7 : 7 )  x 3   = 1  x  3  =  3

Ces deux exemples nous incitent à penser que :

Si on multiplie une fraction par un nombre égal à la valeur de son dénominateur , on obtient son « numérateur ».

C’est ce que nous allons prouver en utilisant des  lettres représentant n’importe quels entiers :

·        « a » et « b » désignant des nombres entiers quelconques   ( avec « b »  0 ) ,  ( b : b )  x  a = 1 x a   = a   , en définitif  on écrira  :

Grâce à ce qui précède, on peut écrire 

A la vue de cette égalité  , on peut dire que   est le nombre qui multiplié par « 3 » donne « 15 ».

Or, vous savez que le seul nombre ayant cette propriété est le quotient de « 15 »  par « 3 » ; c'est-à-dire « 15 : 3 »  qui est égal à « 5 ». On peut donc écrire que «  =  15 : 3 »

·        D’une manière générale , « a » et « b » désignant des entiers quelconques ( avec « b »  0 ) ,   est le nombre qui multiplié par « b » donne « a ».

Or le seul  nombre ( s’il existe) ayant cette propriété est le quotient de « a » par « b » ; on peut donc écrire :

Activités : 

 =   21 : 3  =

=

=

 =   

=

=

 = 

=

=

·        Dans le cas de    , nous posons la division….

Vous constatez que cette division ne se termine pas. (expliquez oralement pourquoi).

  ne peut pas s’écrire sous forme de nombre à virgule car il aurait une infinité de chiffres après la virgule.

Mais on continu d’écrire que le quotient de « 3 » par « 7 » est .

 n’est pas un nombre décimal.  ( on lui donnera le nom de « rationnel »)

3

0

7

2

0

0,42857142

6

0

4

0

5

0

1

0

3

0

2

0

6

Résumé : Voici deux façons de calculer le produit d’un nombre par une fraction :

Vous venez  de voir  que «  =  a : b » . par exemple  «   = 3 : 4 = ………..»

4°)  Fractions décimales.  ( info +++ sur la fraction décimale)

On appelle « fraction décimale »  toute fraction dont le dénominateur est un entier qui s’écrit avec « 1 » suivi de un ou plusieurs zéros. ( 10 ; 100 ; 1 000 ; etc…)

Exemples :

  se lit « un dixième »

  se lit « un centième »

  se lit « un centième »

Vous avez vu au chapitre « 3 »  précédent  que toute fraction peut être considérée comme un quotient. Ainsi :

Ainsi :    =  4 : 10  =  0,4

  =  28 : 10  =  2,8

Vous savez diviser un entier par « 10 » ; « 100 » ;  «1 000 »  ;etc.    ( voir cours …sur diviser un entier par « 10 » ; « 100 » ; « 1 000 »….)

= ….. : ….= ……..

= ….. : ….= ……..

= ….. : ….= ……..

= ….. : ….= ……..

Si vous choisissez d’autres exemples , vous constaterez toujours que :

Toute fraction décimale est une  écriture d’un nombre décimal.

Activité : ….Donnez une écriture « à virgule » des nombres suivants :   ( voir : nombre décimal )

 = ……………

= ……………

= ………….

 = ……..

= ……..

= ……..

Inversement :   Nous allons chercher si un nombre décimal peut s’écrire sous forme de fraction décimale.

·        « 3,8 » peut être considéré  comme le quotient de « 38 »   par « ….10… »

En effet :   3,8  x  …10…… = 38   donc   «  3,8   =  »         ;   réponse : «  3,8  =  »

·        « 0,07 » peut être considéré comme le quotient de « 7 » par    «  …100… »

En effet :   0,0 7  x  …100…… = 7   donc   « 0,0 7   =  »         ;   réponse : «  0,07  =  »

Si vous choisissez d’autres exemples , vous constaterez toujours que :

Tout nombre décimal peut s’écrire  sous forme de fraction décimale.

Info 1 + transformer un N en fraction décimale

Info 2  + transformer un décimal  en fraction décimale

Activité ….. :

En complétant le numérateur , donnez une écriture fractionnaire des nombres suivants.

8,7 =

0,03 =

0,639 =

3 = =

5 =

26 =

1,5 =

7,4 = =

1 =

4683=

0,3 =

0,04=

Remarque :Certaines fractions « non décimales » sont des écritures de nombres décimaux .

Exemples :

= …….

= ……………………..

= ……………………..

Donnez une écriture à virgule  des nombres suivants :

= ……………

=……………..

=………………..

=……………

=……………….

Activité …. : Range dans l’ordre croissant les nombres  suivants  ( en utilisant le signe  )                                       ( liste de formulaires)

5°)  Fractions représentant le même nombre.         ( voir1 : fraction équivalente) ; ( voir 2 : les suites de nombres rapports égaux ; proportionnelles.) ; ( voir cours de 4^ème collège)

I )  Fractions égales dite « équivalentes »

Activité ……. : 3 personnes mangent de la tarte.

1°) La tarte est partagée en « 4 » morceaux  « identiques ».

Si chaque personne prend un morceau, au total :  de la tarte est consommée.

2°) La tarte est partagée en « 8 » morceaux  « identiques ».

Il y a deux fois plus de morceaux qu’à l’exercice précédent.

Si chaque personne mange autant qu’ au précédent ,elle prendra « 2 »  morceaux.

 au total : de la tarte est consommée.           ………..  ( )

3°) La tarte est partagée en « 12 » morceaux  « identiques ».

Il y a ……( 9 )….. fois plus de morceaux qu’à l’exercice N°1.

Si chaque personne mange autant qu’ au précédent ,elle prendra « 3 »  morceaux.

 au total :  de la tarte est consommée.           ………..  ( )

·        Conclusion :  Dans les trois cas la partie consommée est la même .

·        Donc :  ;  ;  sont des écritures différentes d’un même opérateur.

On peut écrire alors :   =  =

·        Vous constatez que :    ;  

·        Trouvez d’autres fractions représentant ce nombre :

Corrigé :

Activité ……. :complétez les égalités suivantes  ( vous considérez que LN  on la même longueur)

LP  =   LN

LP  =   LN

LP  =   LN

On peut dire que   ; …… ; ……..représentent le même nombre. ON écrit = ………..= …….

Trouvez d’autres fractions  représentant ce nombre :

A retenir :

Etant donné une fraction, on obtient  une autre fraction ( fraction équivalente)  représentant le même nombre en multipliant  ou en divisant  ( quand cela est possible )les deux termes de cette fraction par un même entier non nul.

Activité ….. :

II ) Simplification de fraction.     ( simplifier une fraction @  )

« Simplifier » une fraction consiste à la remplacer par une fraction représentant le  même nombre et telle que ses deux termes soient des entiers plus petits .

Procédure : pour simplifier une fraction on divise ses deux termes par un entier , si , possible le plus grand possible.  ( lorsque l’on a trouvé le plus grand diviseur , on dira que la fraction est rendue  irréductible)

Exemples :

Simplifions  

Simplifions  

Suite :

=

=

= 

=

=

=

=

Situations problèmes :  ( info +++  autres exemples)

N°1 : Une citerne contient   1 500 Litres de vin.

On en vide les 2 / 5  puis les 3 / 4  du reste.

Quelle quantité de vin reste-t-il dans la citerne ?

N°2 : Une voiture neuve coûte  34 300 € .

Chaque année, cette voiture perd les  2 / 7 de ce qu’elle valait l’année précédente .

Combien vaudra – t- elle dans 3 ans ?