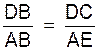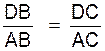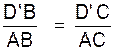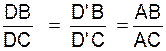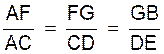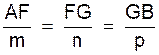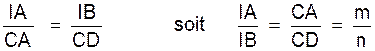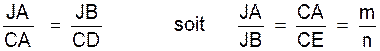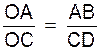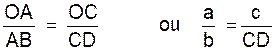.

 Géométrie :  DOSSIER : THALES   / 

Pré requis

Les triangles semblables et homothétiques

L’homothétie

ENVIRONNEMENT du dossier

INDEX    

Objectif précédent :

Les pré requis  

2°) Cours de niveau V

Objectif suivant :

:1°)Interdisciplinarités

2°) division de segments.

3°) les triangles homothétiques.

Tableau      

2°)Liste des objectifs

DOSSIER : APPLICATIONS  du  THEOREME DE THALES

1.  Propriété des bissectrices d’un triangle.

2.  Construction :

-        Partage d’un segment en parties proportionnelles

-        Construire les points qui divisent un segment dans un rapport donné.

-        Quatrième proportionnelle à trois segment.

TEST

COURS

Devoir  Contrôle

Devoir évaluation

Interdisciplinarité                 

Corrigé Contrôle 

Corrigé évaluation 

:Evaluation diplômante :Contrôle Continu : Thalès

COURS

Info @ « bissectrice.

Propriété des bissectrices d’un triangle

Info1@.

Info 2 @

Info 3 @

Théorème : la bissectrice intérieure d’un angle d’un triangle divise  le côté opposé  en segment additifs proportionnels aux côtés adjacents.

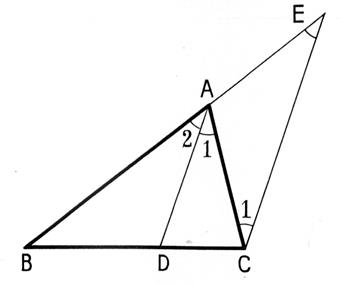
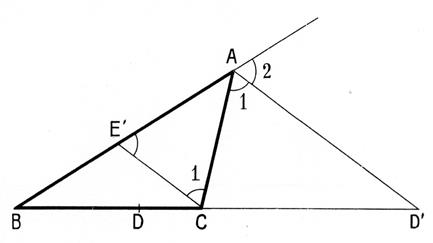
Soit AD  la bissectrice intérieure de l’angle A du triangle ABC ( ci contre).

Menons par le point « C » une parallèle à DA . Elle coupe le prolongement de BA en E . Nous avons :

L’angle C₁ =  l’angle A₁ comme alternes internes.

L’angle E  =  l’angle A₂  comme correspondants.

L’ angle A ₁  est égal à l’angle A ₂ il en résulte que l’angle C₁ est égal à l’angle E .

Le triangle ACE est isocèle et     AC = A E.

Or , d’après le théorème de Thalès appliqué au triangle BCE et à la parallèle  AD au côté EC :

Soit en remplaçant AE par son égal AC :  

Théorème : La bissectrice extérieure d’un angle d’un triangle divise la côté opposé en segments soustractifs proportionnels aux côtés adjacents.

La démonstration est analogue .Il faut remplacer simplement D et E par D’ et E’ . On obtient :

remarque : d’après les théorèmes précédents nous pouvons écrire :

Nous voyons ainsi que :

Les pieds des bissectrices d’un angle d’un triangle sont les points qui divisent intérieurement et extérieurement le côté opposé dans le rapport des côtés adjacents.

CONSTRUCTIONS :

(info @ : divisions de segment)

1°) Partage d’un segment en parties  non égales  mais  proportionnelles.

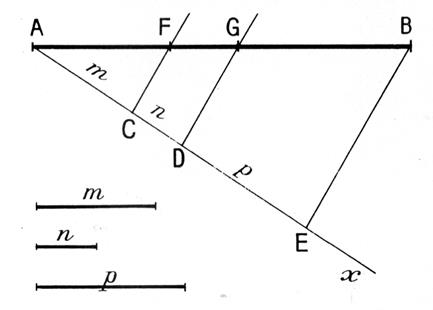
Soit à partager le segment AB en parties proportionnelles  aux segments  de longueurs données : « m » , « n » et « p » ( ci dessous).

Sur une  demi droite droite auxiliaire Ax , portons   successivement les segments  AC , AD et DE  égaux respectivement à « m » , « n » et « p ». Joignons EB  et menons  par C et D  les parallèles à EB. Elles coupent AB en F  et G . D’après le théorème de  Thalès on a :

soit

2°) Construire les points  qui divisent un segment dans un rapport donné :

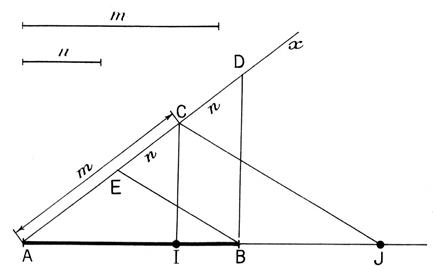
Soit à construire les points qui divisent intérieurement et extérieurement les segment AB dans le rapport :

de deux segments donnés. Sur une  demi- droite auxiliaire quelconque Ax portons AC = m ; et CD = CE = n.

Joignons BD et DE et par C menons les parallèles à BD et BE.

Ces parallèles coupent respectivement la droite  AB en I et J  .

D’après le théorème de Thalès on a :

Quatrième proportionnelle à trois longueurs

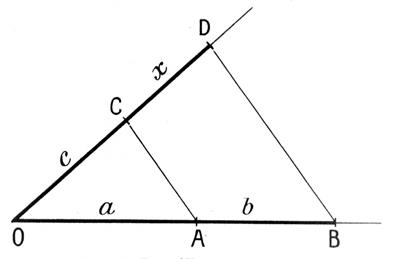
Soient « a » , « b » , et « c » les trois longueurs données. Sur l’un des côtés d’un angle , portons

    OA = a et AB = b .

Puis sur le second côté portons

           OC = c .

Joignons AC et B menons la parallèle à AC . Elle  coupe OC en D .

D’après le théorème de Thalès on peut écrire :

soit :

Le segment « x » = CD est la quatrième proportionnelle  à « a » , « b » et « c » .

CONTROLE :

Enoncé le théorème de Thalès ; vous  vous aidez  d’un dessin pour « expliquer ».

Etablir les rapports .

EVALUATION

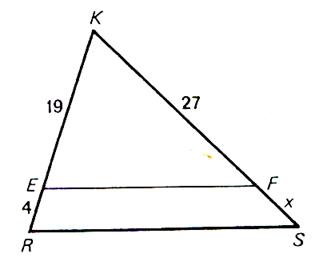
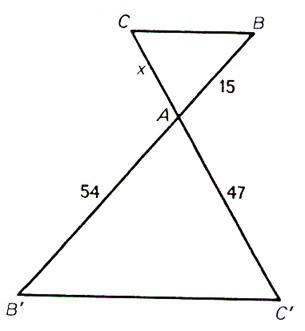
N°1 : Calculer « x »

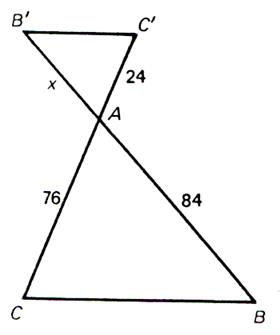
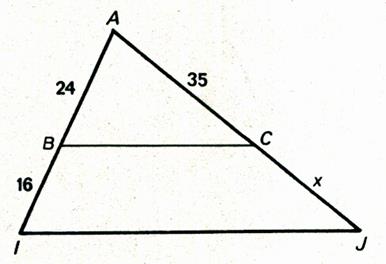
N°2 :

Calculer « x »

N°3 :

Calculer « x »

N°4 :

Calculer « x »

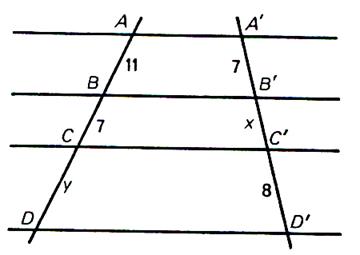
N°5 : Calculer « x »  et « y »

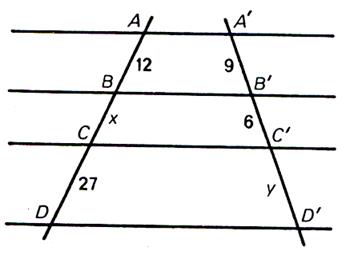
N°6 : Calculer « x »  et « y »