Pré requis:

Les projections

Le triangle

Les triangles homothétiques  ( le rapport d ’ homothétie )

ENVIRONNEMENT du dossier:

Index  warmaths

Objectif précédent :

1°) La propriété de Thalès

2°) INFO complète.

Retour au sommaire

THALES :sommaire  

DOSSIER : THALES : Propriétés dans le triangle .

1° )Propriétés de Thalès dans le triangle : propriétés  directe et indirecte.

2°) Théorème des milieux :   direct  et   Théorème réciproque :

3°)  GENERALISATION :     A l’ensemble des côtés (3)

4°)   Démonstration

COURS

Devoir  Contrôle

Devoir évaluation

Interdisciplinarité

Corrigé Contrôle  

Corrigé évaluation  

COURS

1°)    Propriétés de Thalès dans le triangle :

Propriété directe :

Info plus ++++

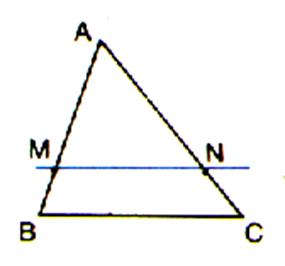
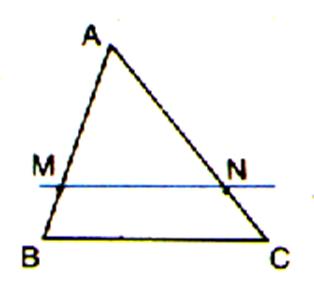
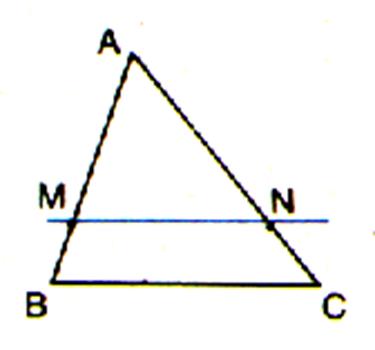
Dans un triangle ABC si (MN) est parallèle à (BC) alors :

Propriété réciproque

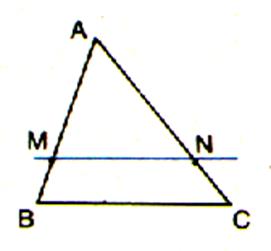
Dans un triangle ABC si  alors (MN) est parallèle à (BC)

2°)   Théorème des milieux :

Théorème direct

Info plus +++++

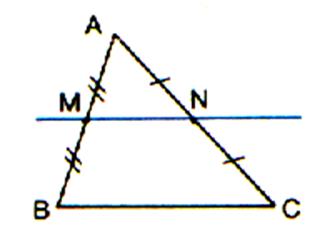
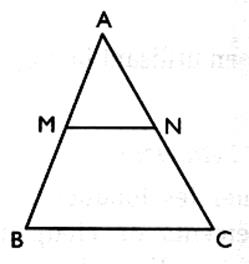
Dans un triangle , la droite qui passe par le milieu d’un côté et qui est parallèle à un autre côté coupe le troisième en son milieu .

(MN) est parallèle à (BC) et M milieu de [AB]  Þ N milieu de [AC]

démonstration :

(MN) // (BC) Þ   et  M milieu de [AB] Þ ;

donc

d’où N milieu de [AC] .

Théorème réciproque :

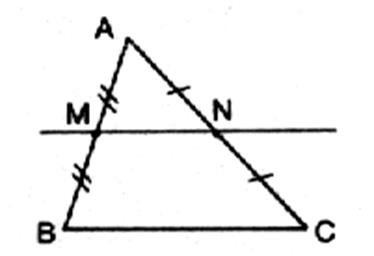
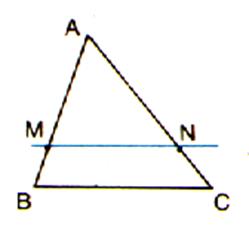
Dans un triangle la droite qui passe par les milieux de deux côtés est parallèles au troisième côté

M est milieu de [AB] et N milieu de  [AC] donc (MN) // (BC)

3°)  GENERALISATION :

A l’ensemble des côtés (3)

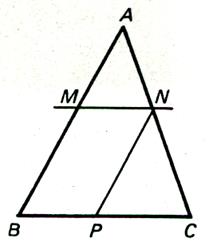
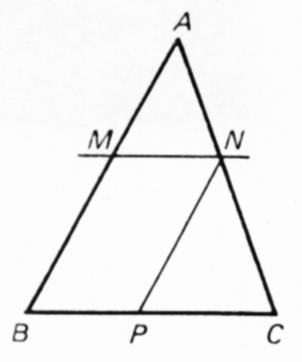
Soit un triangle ABC , et les points M et N des côtés AB et AC.

Si (MN) est  // à (BC) alors :

Les côtés des triangles  ACB et ANM  sont proportionnels

4°)   Démonstration

(MN) // (BC) Þ

la droite parallèle à (AB)  passant par N coupe BC au point P.

(NP) //(AB) Þ

Permutons les moyens de la proportion:

Þ

D’après la propriété sur le partage proportionnel  , nous pouvons écrire :

MNBP est un parallèlogramme donc

BP= MN

Des relations précédentes nous pouvons en déduire que:

En permutant les extrêmes , nous obtenons :

Des égalités :  et

Nous en déduisons :      

Fin de  la démonstration !

TRAVAUX AUTO FORMATIFS.

CONTROLE:

1°)Citer la propriété de Thalès et sa réciproque

2°) Citer le théorème des milieux et sa réciproque.

a)    Théorème direct

b) Théorème réciproque :

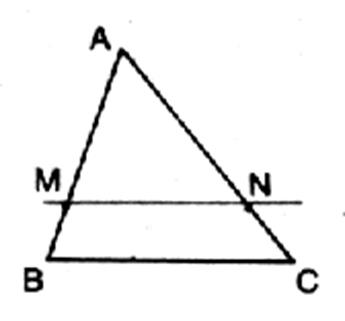
3°) Soit un triangle ACB , une droite  parallèle à (BC) coupe les cotés [AB]    [AC] respectivement en M et N alors : établissez  les rapports

EVALUATION:

Série 1 :

1°) Dans un triangle ACB , le segment MN est parallèle  au segment  BC .

a)    On donne AN = 8  , AC = 12 et AB = 15 . Calculer AM.

b)   On donne   AM = 4 , AB = 5  et AN = 5 . Calculer AC.

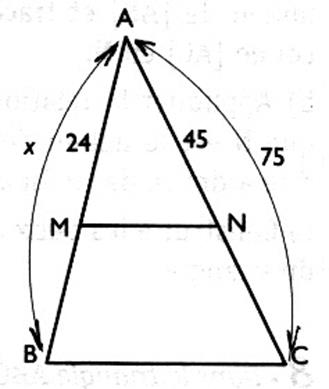
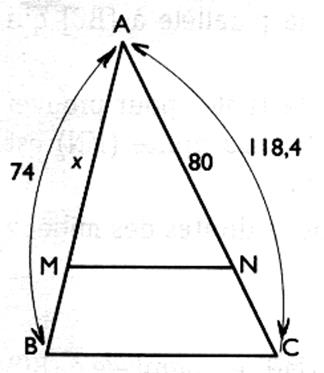
2°) Dans le triangle ACB , la droite ( MN ) est parallèle à la droite ( B C ) .Calculer la longueur  " x " .

3°) Dans le triangle ACB , la droite ( MN ) est parallèle à la droite ( B C ) .Calculer la longueur  " x " .

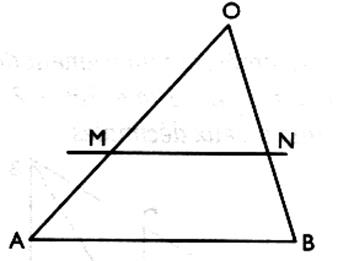
4°) Sachant que ( AB)  est parallèle à  ( M N ) .On demande de calculer  OM lorsque ON = 14  ; OA = 27 et OB = 21 . En déduire que MA et NB .

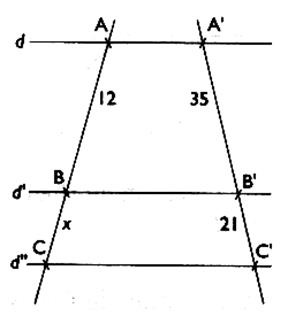
Vérifier que les rapports  MA / NB = OM / ON = OA / OB .

5°) Calculer la longueur "x" , sachant que les droites  d , d'  et d"  sont parallèles ; Les dimensions sont en mm .

Série 2 : PROBLEMES :

1°) Droite des milieux d' un  triangle .

a)    Construire un triangle de côtés  AB = 6 cm , BC = 7 cm et AC = 8 cm . Placer le point M au milieu du segment [ AB ] et tracer la parallèle à [ BC]  qui coupe [A C]  en N .

b)Appliquer la relation de Thalès  pour prouver que N est le milieu de  [ AC] . La droite  ( MN ) est dite  « droite des milieux » .   

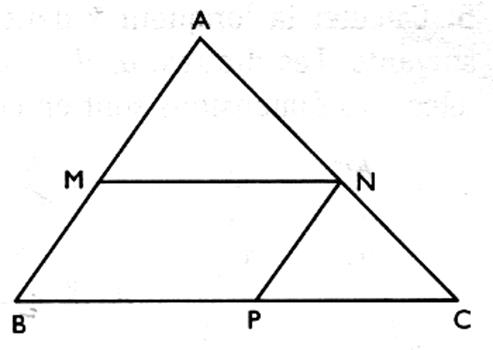
b)   Construire les deux autres droites des milieux du triangle .

 2°) Dans un triangle ACB , on trace  le segment MN parallèle  au segment BC et le segment NP parallèle au segment AB . On donne

AB = 5 ; BC = 7 ; AC = 6 et AM = 3

répondre aux question suivantes :

a)    calculer AN en appliquant la relation de Thalès au triangle ABC coupé  par  MN . En déduire CN .

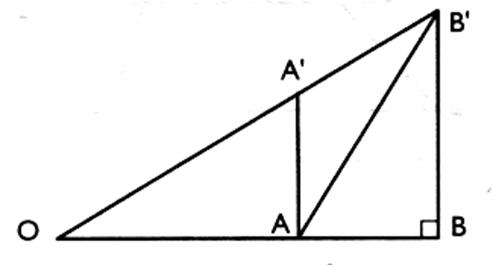
b)   Calculer CP en appliquant la relation de  Thalès au triangle CBA coupé par le segment NP. En déduire BP .

c)    Quelle est la nature du quadrilatère MNPB ? En déduire MN .

d)   Calculer le rapport  MN / BC .

Vérifier que l’on a :

3°) La figure ci - dessous représente un  élément  de charpente  pour lequel on a : OA = 3 m et BB’ = 2,6 m . Arrondir les résultats au cm près .

a) calculer  dans le triangle  rectangle  ABB’ :   la longueur de AB pour que AB’=AO.

b) Calculer la longueur OB puis OB’ dans le triangle B’BO .

c)    Sachant que  A’A est parallèle à B’B  , calculer  A’A en utilisant le résultat de la question précédente .

d)   Calculer A’O en utilisant la propriété de Thalès .

Série 3 :  en utilisant  « Thalès et Pythagore » .

On doit calculer les différentes longueurs des pièces des éléments de charpente ci - dessous . Pour cela , il faut appliquer soit la propriété de Thalès et  / ou la propriété de Pythagore .

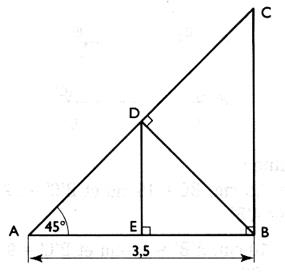
Les longueurs sont indiquées en mètres . On arrondira les résultats au cm près . ( on dit aussi : à deux décimales )

1°) soit la figure ci - dessous :

a)    calculer l’angle C .

b)   Quelle est la position de D sur le segment  AC et de E sur le segment AB ?

c)    Calculer les longueurs   des segments : BC , AC , BD et DE .

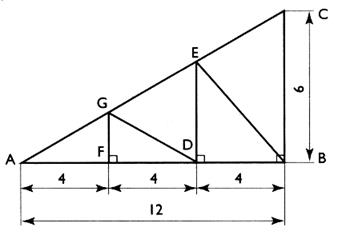
2°) soit la figure ci - dessous :

a)    calculer la longueur du segment AC .

b)   On connaît la position des points F et D sur le segment AB , en déduire  celle des points  G et E sur  le segment AC .

c)    Quelle est la nature du triangle  GDA ?

d)   Calculer les longueurs des segments : AG , GE , EC , GD , GF , ED et EB.