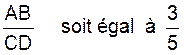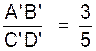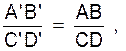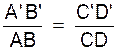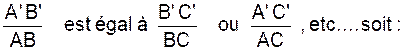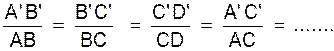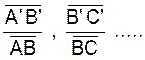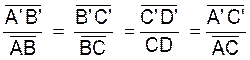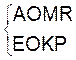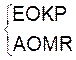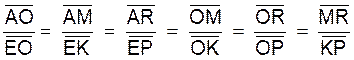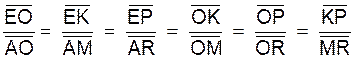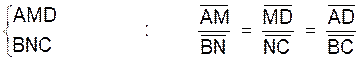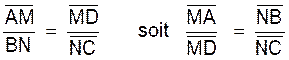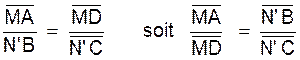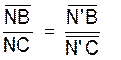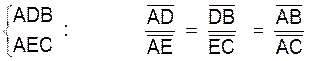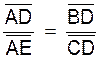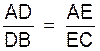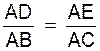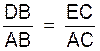Théorème de Thalés_démonstration.

Ce qu ‘il faut savoir sur le théorème : ce théorème rend compte , en fait , de propriétés à peu prés évidente qu’ont des droites parallèles quand elles en coupent deux ou plusieurs autres.

La notion fondamentale qui est en jeu est celle de « rapport » , et le théorème énonce l ’ égalité de deux rapports , donc met en jeu une « proportion ».

(Stella BARUK , Dictionnaire des Mathématiques élémentaires ;ed. Seuil , page 1193)

THALES et le THEOREME de THALES

Qui est « THALES » ?

Thalès de Millet.

Il vécut environ 600 ans avant J.C.

Il est né en Grèce au VIIième siècle avant J.C. . Mathématicien et philosophe grec , on lui attribua la première mesure « exacte » du temps, il aurait apporté d ’ Egypte en Grèce les fondements de la géométrie.

Travaillant sur les lignes (droites, cercles ,angles ) il donna son point de départ à la géométrie pure :il fut le premier à démontrer que le diamètre d’un cercle partage celui-ci en deux parties égales , que tout angles inscrit dans un demi cercle est droit , que deux angles opposés par le sommet sont égaux .

On suppose qu’il fut le premier à bâtir des démonstrations élémentaires à partir d ’ axiomes.

Quelques définitions :

« Axiomes » un axiome est un énoncé évident par lui même et donc non susceptible d’être démontré.

Exemples d’axiomes d ’ Euclide :

On peut ajouter ou soustraire la même quantité à deux quantités égales .Les quantités obtenues sont alors égales.

Deux quantités égales à la même quantité sont égales entre elles.

Postulat : Le postulat est un principe premier , indémontrable ou non démontré , dont l’admission est nécessaire pour établir une démonstration.

Exemples de postulats d’Euclide.

Par deux points passe une droite.

Un cercle est déterminé par la connaissance de son centre et de son rayon.

Tous les angles droits sont égaux .

Par un point extérieur à une droite , on peut mener une et une seule droite parallèle à cette droite.

Définition de « Théorème » : du latin theorema , du grec théôrêma , « ce qu ‘on peut contempler »

d’après le Littré :

« théorème » : terme didactique, consiste en « toute proposition qui a besoin d’une démonstration pour devenir évidente »

Le théorème est un énoncé « vrai » dans une théorie mathématique donnée .Leur vérité a été établie , ils sont à redémontrer.(et non pas « à démontrer »)

Première approche du
Théorème de Thalès

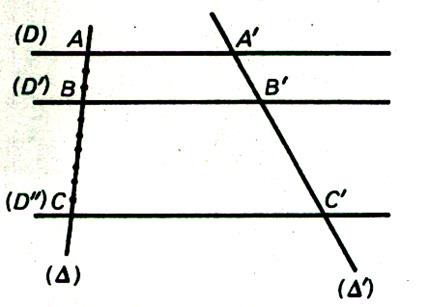
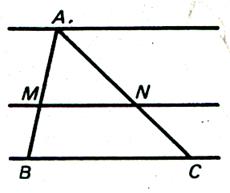
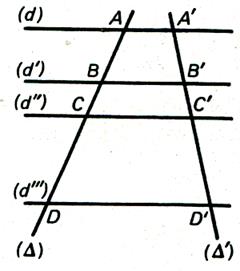
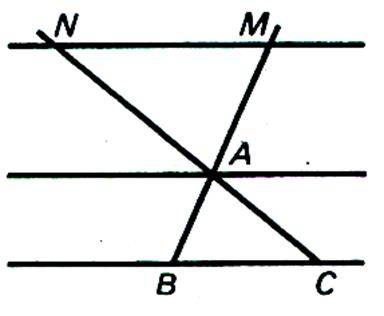
Soit 3 droites parallèles ( D) , (D ’) et ( D ’’) coupées par deux droites sécantes ( D) et (D’) ; nous comparons les rapports : et

Partageons AB en trois parties et BC en sept parties

tal2

Deuxième approche du
Théorème de Thalès :

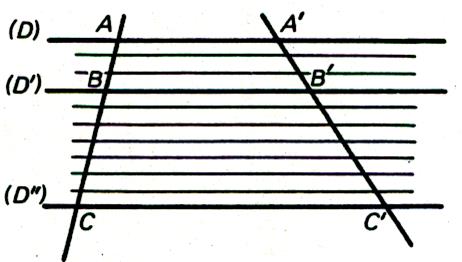
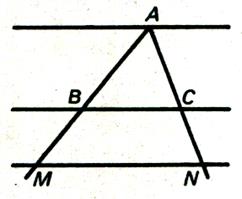
Soient AB et BC tels que (1)

Les parallèles ( D) , (D ’) et ( D ’’) menées par les points de division de AB et BC forment avec ( D) , (D ’) et ( D ’’) un ensemble de parallèles équidistantes découpant (D’) des segments consécutifs égaux : 3 sur A’B’ et 7 sur B’C’ ,

tal1

(2)

ainsi de (1) et (2) nous montrons que

Dans cette proportion nous pouvons permuter les moyens : ( info CD ++ « moyen »)

On retiendra :

Trois parallèles découpent sur 2 sécantes des segments correspondants proportionnels .

tal6

Enoncé général : lorsque des droites sont parallèles , elles déterminent sur deux sécantes quelconques des segments correspondants proportionnels.

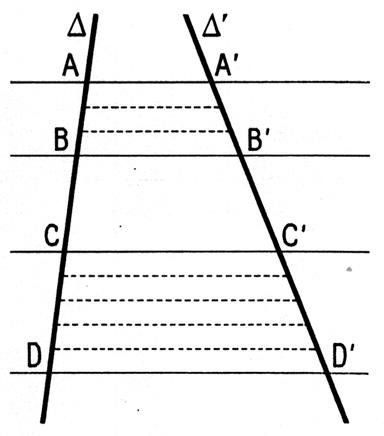
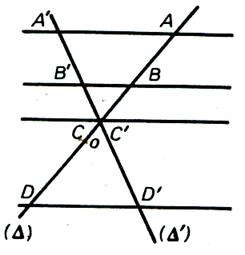
Soient AB et CD deux segments déterminés sur la sécante Δ , A’B’ et C’ D’ les segments correspondants déterminés sur Δ ‘ ( figure ci contre ) par les parallèles AA’ , BB ’ , CC ‘ , DD’ . Supposons que .

Nous pouvons donc partager AB en 3 segments et CD en 5 segments , de telle sorte que les 8 segments ainsi obtenus soient égaux . Par les points de division, menons les parallèles à AA’ , BB ‘ …Ces parallèles partagent A’ B’ et C’ D’ en segments égaux. En effet , si des parallèles déterminent des segments égaux sur une sécante , elles déterminent des égaux sur toute autre sécante.

Il y a 3 de ces segments sur A’ B’ et 5 sur C’ D’ . D’où : nous en concluons que soit en permutant les moyens : .

On démontrerait de même que

Remarque : Nous pouvons supposer que les sécantes Δ et Δ ‘ sont orientées. Les mesures algébriques des vecteurs de même sens , et sont de même signe et celles des vecteurs , et le sont également.

Les rapports : tels que égaux en valeur absolue , ont donc le même signe et nous pouvons écrire :

Comment écrire les rapports égaux du théorème de THALES ( ?) :

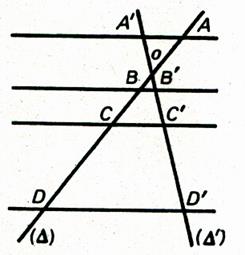
Les deux termes de chaque rapport doivent contenir au numérateur un segment de la première sécante et au dénominateur le segment correspondant de la seconde .. Si on considère les rapports algébriques , il faut de plus, que les extrémités correspondantes de ces segments soient énoncées dans le même ordre.

Exemple : Dans la figure ci contre les sécantes Δ et Δ’ se coupent en « O » . Nous pouvons toujours supposer qu’une parallèle passe par « O ».

Sur Δ :

nous notons ordonnés les points :AOMR

Sur Δ’ : nous notons ordonnés les points :BOKP

Il est facile d’écrire le système suivant :

ou le système

En mettant sur une ligne les points de Δ et au dessous les points correspondants de Δ ‘ (ou inversement) . Les segments de chaque rapport se correspondent ainsi verticalement ;Nous obtenons les deux suites de rapports égaux suivantes :

Application au trapèze : Première forme particulière du théorème de Thalès.

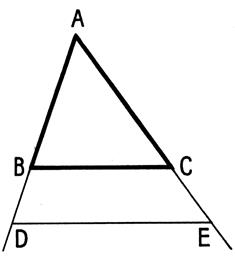
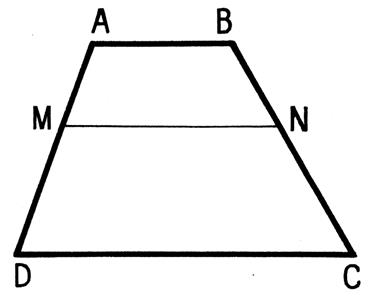
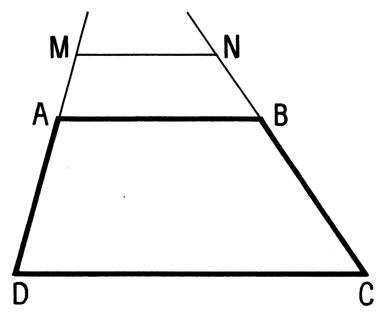
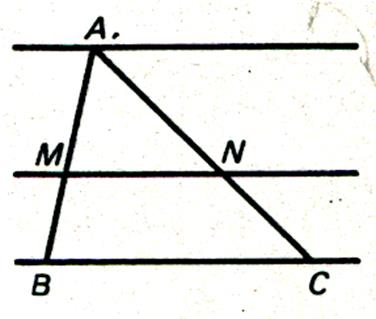
Toutes parallèle aux bases d’un trapèze détermine sur les côtés non parallèles des segments proportionnels.

Soit les deux figures suivantes :

Quel que soit le cas proposé nous obtenons ainsi trois parallèles AB , MN et DC coupées par deux sécantes AMD et BNC. Donc :

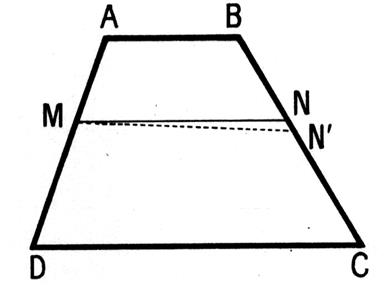
Réciproque : lorsqu’une sécante détermine des segments proportionnels sur les côtés non parallèles d’un trapèze , elle est parallèle aux bases.

Soit le trapèze ci contre ABCD et un sécante MN qui coupe AD en M et BC en N de telle sorte que :

(1)

Par le point « M » menons la parallèle aux bases qui coupe BC en N’. D’après le théorème « direct » nous avons :

(2)

En rapprochant les égalités (1) et (2) nous obtenons :

Cette égalité montre que « N » et « N’ » partagent le segment « BC » dans le même rapport algébrique. Ces deux points sont confondus car , il n’existe qu’un seul point divisant un segment dans un rapport algébrique donné.

Donc MN est ^parallèle aux deux bases AB et CD .

Remarque : sur la disposition des points : si l’on ne considère que des rapports arithmétiques , il faut dans cette réciproque vérifier que les points M , A et D d’une part , N B et c d’autre part ont bien la même disposition.

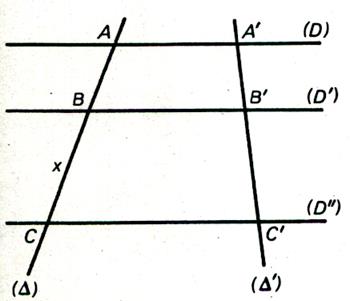
CALCULS : APPLICATION :

AB = 15 cm , A’B’ = 12 cm ; B’C’ = 20 cm . Calculer « x »

Solution : on pose : on remplace :

Calculs : on transforme x ´ 12 = 15´ 20

x = ;

x = 25 cm

Deuxième forme particulière du théorème de Thalès.

Appl ication au triangle

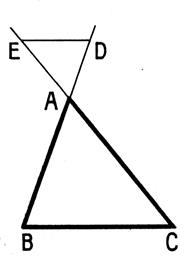
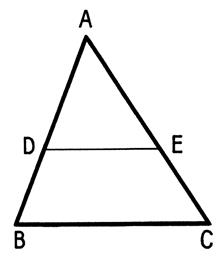
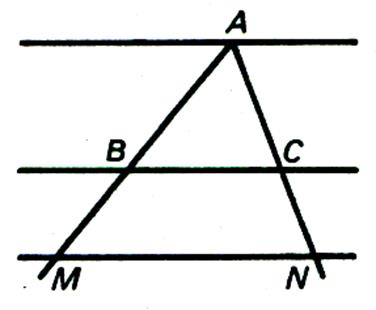
Toute parallèle à l’un des cotés du triangle détermine sur les deux autres côtés des segments proportionnels .

Soit les 3 figures ci dessous :

Figure 1

Figure 2

Figure 3

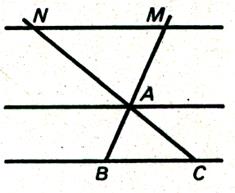
Si nous observons ces figures , nous avons sur les sécantes ADB et AEC :

Nous pouvons établir les rapports communs aux 3 :

(1)

Réciproque : : lorsqu ‘une sécante détermine des segments proportionnels sur deux côtés d’un triangle , elle est parallèle au troisième côté .

Il suffit de reprendre la démonstration relative au trapèze (@ info) en supposant « B » confondu avec « A » . Ainsi , lorsque dans un triangle ABC (Figure 1ci dessus) on a :

la droite DE est parallèle à BC .

Remarque ; on écrit souvent les relations du théorème de Thalès appliqué sous l’une des trois formes

Chacune de ces proportions s’obtient en échangeant les (@) moyens dans les proportions résultant des relations (1) ci dessus.

On peut établir pour les 3 cas suivants : les rapports ci dessous.

D’après le théorème de Thalès :

EXEMPLES de CALCULS

Exemple 1 :

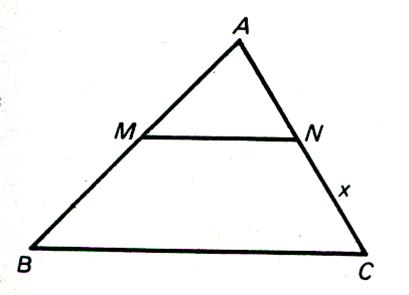
Connaissant AM= 7 cm ; MB = 5 cm et AN = 4 cm . Calculer NC.

Le théorème de Thalès appliqué au triangle nous donne :

Calculs : on transforme x ´ 5 = 4´ 7

x = ;

x = 5,6 cm

tal11

¨Exemple 2 :

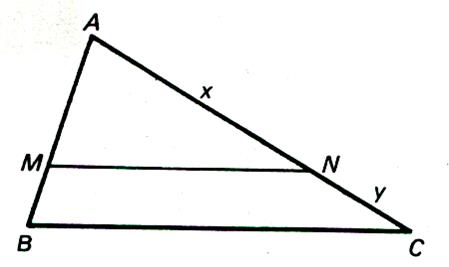
Connaissant AB = 13 mm ; MB = 3 mm ; AC = 40 mm , calculer « x » et « y ».

tal10

Solution :

; transformation x = 13 ´ 2,5 ; x = 32,5 mm

; transformation y = 3 ´ 2,5 ; y = 7,5 mm

3°) Généralisation sur l’écriture des rapports.

Appliquons le théorème de Thalès 3 droites parallèles ( d) , (d ’) et ( d ’’) coupées par deux droites sécantes ( D) et (D’)

tal7

tal9

tal8

De même pour ( d) , (d ’) et ( d ’’) coupées par deux droites sécantes ( D) et (D’) .

Et cela implique que :

Mais on a aussi : =

Des parallèles découpent sur 2 sécantes des segments correspondants proportionnels .

TRAVAUX AUTO FORMATIFS.
CONTROLE : Enoncé le théorème de Thalès ; vous vous aidez d’un dessin pour « expliquer ».
Etablir les rapports .

EVALUATION
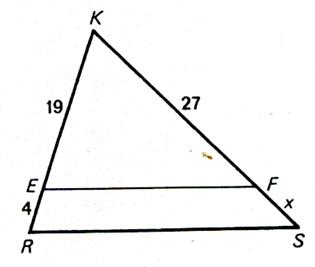
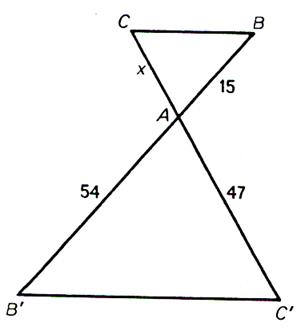
N°1 : Calculer « x »
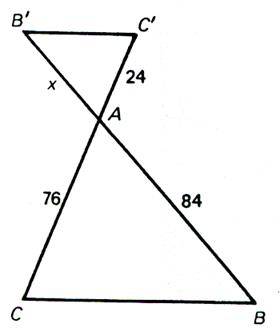
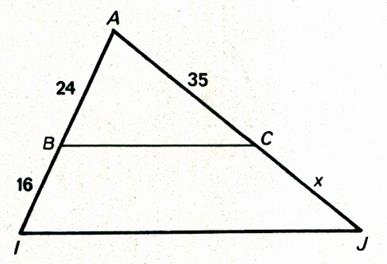
N°2 : Calculer « x »
N°3 : Calculer « x »
N°4 : Calculer « x »
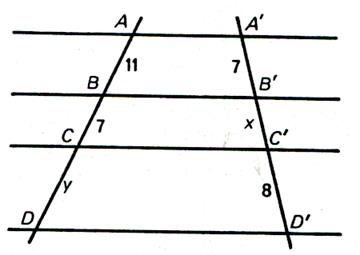
N°5 : Calculer « x » et « y »
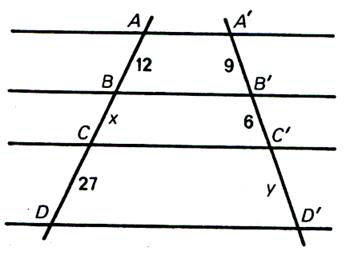
N°6 : Calculer « x » et « y »

EVALUATION