Pré requis
|
Les triangles semblables ;…. |
|
|
Les grandeurs proportionnelles (résumé) |
|
|
Droites milieux dans un triangle |
|
Objectif précédent : |
Objectif suivant : |
Liste des cours sur « Thales » |
|
|
|
|
|
|
DOSSIER THALES : Pré requis N°2
|
|
1°) Outils mathématiques utilisés: |
|
|||||
|
|
2°) Qui est « THALES » ? |
|
|||||
|
|
3°) THALES et le THEOREME de THALES
. ( à quoi ça sert ?...) |
|
|||||
|
|
|
||||||
|
|
|
|
|||||
|
|
5°) OBTENTION D’UNE DIVISION IRREGULIERE ou REGULIERE D’UNE DROITE |
|
|||||
|
|
|
|
|||||
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
COURS |
Devoir Contrôle |
Devoir évaluation |
|
|||
|
|
INFO :COURS : |
|
|
|
|
|
|
|
1°) Outils
mathématiques utilisés: |
|
|
|
- La suite de rapports égaux ( savoir
établir) - Calcul : le rapport
égal ( savoir
choisir ,dans une suite de rapports égaux
les deux rapports , dont on
connaît trois valeurs sur quatre) :
modèle : exemple : : il nous suffit de trouver la
« quatrième » proportionnelle ; ce qui donnera pour « a » = 3
fois 12 divisé par 9 =
4 ; et pour « b »
= 8 fois 9 sur 3 = 24 |
|
|
|
2°) Qui est « THALES » ? Thales de Millet. Il est né en Grèce au VIIième siècle avant J.C. .
Mathématicien on lui attribua la première mesure « exacte » du
temps, il aurait apporté d ’ Egypte en Grèce les fondements de la
géométrie. Travaillant sur les lignes
(droites, cercles ,angles ) il donna son point de départ à la
géométrie pure :il fut le premier à démontrer que le diamètre d’un
cercle partage celui-ci en deux parties égales , que tout angles inscrit dans
un demi cercle est droit , que deux angles opposés
par le sommet sont égaux . On suppose qu’il fut le premier à bâtir des démonstrations
élémentaires à partir d ’ axiomes. Quelques définitions : « Axiomes » un axiome est un énoncé évident par lui même et donc non susceptible d’être démontré. Exemples
d’axiomes d ’ Euclide : On
peut ajouter ou soustraire la même quantité à deux quantités égales .Les
quantités obtenues sont alors égales. Deux
quantités égales à la même quantité sont égales entre elles. Postulat : Le postulat est un principe premier , indémontrable ou non démontré , dont l’admission
est nécessaire pour établir une démonstration. Exemples
de postulats d’Euclide. Par deux points passe une droite. Un
cercle est déterminé par la connaissance de son centre et de son rayon. Tous
les angles droits sont égaux . Par
un point extérieur à une droite , on peut mener une et une seule droite parallèle à cette droite. Définition de « Théorème » :
du latin theorema , du grec théôrêma ,
« ce qu ‘on peut contempler » d’après le Littré :
« théorème » : terme didactique, consiste en
« toute proposition qui a besoin d’une démonstration pour devenir évidente » |
|
|
|
3°) THALES et le THEOREME de THALES |
|
|
|
|
|
|
|
A
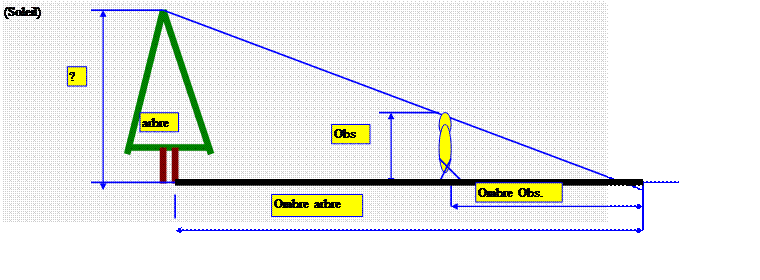
quoi sert le théorème de THALES. ? Exemple : Calculer la hauteur d’un
arbre : |
|
|
|
|
|
|
|
Par soleil :
On connaît la hauteur de l’Observateur
(1,80 m) On mesure la
longueur de l’ombre de l ’ arbre au sol.
L’Observateur se place debout au point de rencontre (affleurement de
la tête) avec l’ombre « portée », on mesure la distance qui sépare
l’Observateur et le point de rencontre
des ombres (point le plus éloigné de l’ombre de l’arbre ) : On établit la relation de proportion :
si hauteur de l’observateur =
1,80 ; Ombre Observateur 3 m : ;longueur
de l’ombre de l’arbre 42 m nous remplaçons dans la relation de proportion :
Calcul de la quatrième proportionnelle : hauteur de l’arbre = 1,80 fois
42 divisé par 3 Conclusion : l’arbre à pour hauteur approximative : 25,20 m PAGE RAPPELS : « Image » : on
appelle « image » le représentant d’un élément (Algébrique , ou
géométrique) de l’ensemble de départ « réfléchi » dans l’ensemble
d’arrivée. |
|
|
|
|
|
|
|
A
![]()
 d
d
![]() : est la droite de direction
imposée
: est la droite de direction
imposée
d : est
la droite recevant l’image de A
d
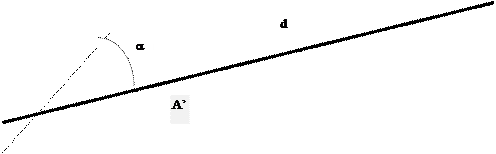
Pour obtenir l’image de A ( A’)
sur la droite « d » , on trace une droite
parallèle à la direction (d )
donnée passant par A et coupant la droite « d », le point
d’intersection est A’ ,
Commentaire : la droite
passant par AA’ , parallèle à « d »
est appelée : projetante
On dit que le point « A’ » est la projection (ou projeté) du point
« A » sur la droite « d » par rapport à « d ».
On dit aussi que : A’ est
l’image de A sur « d » par rapport
à « d ».
Suite : Voir
« projection » d ‘ un
segment.
Aperçu du problème « THALES »
On sait comment diviser un segment en deux parties égales pour cela on
trace la médiatrice.
Mais comment partager un segment AB ,en plusieurs ( 3)
parties « égales » ?

Attention : on demande de diviser un
segment de droite ;( « morceau » de droite
« bornée » )
Autre rappel : sur la graduation régulière ou irrégulière
Vocabulaire : un
segment est une droite bornée.
SUR
la « division régulière ou irrégulière » d ’ une droite
« non » bornée
(travail simple et accessible à tous)
ou
comment diviser une droite en parties non égales ou en parties égales :
a) Construction d’une
« Division irrégulière » sur une droite non bornée :
Procédure :
![]() on trace
une droite :
on trace
une droite :
On choisit l’emplacement d ’ un point sur cette droite et
l’on « coupe » cette
droite en autant de points que l’on veut ;à l’aide d’un
« crayon ».
![]()
Nous pouvons nommer ces points (A ;B ;C ;...)
b) Construction de divisions régulières
sur une droite non bornée. (ou « comment diviser
régulièrement une droite »)
Procédure :
![]() On trace une droite :
On trace une droite :
On prend un compas dont on règle l’ouverture .
On choisi un premier point où
l’on place la pointe du compas
On reporte autant de fois que cela est possible ,
On appelle « division régulière » d’une droite « d »
un ensemble de points de la droite régulièrement espacés.
d D E A B C
![]()
On peut considérer que A,B ,C, D, E est
une division régulière de la droite d
|
|
|
|
5°) OBTENTION D’UNE DIVISION IRREGULIERE ou REGULIERE D’UNE DROITE « BORNEE » à
partir d’une droite divisée régulièrement
(ou irrégulièrement ):
remarque :
pour diviser une droite « D » « bornée » régulièrement
,nous devons ,au préalable , construire un segment de droite régulièrement divisé.
CAS d’une division irrégulière :
Données
de départ :
la droite « D1 »
irrégulièrement graduée en A ;B ;
la
droite « D2 » (droite sur
laquelle on va tracer les divisions)
La droite d
La longueur du segment AB
est différent de la longueur du segment BC
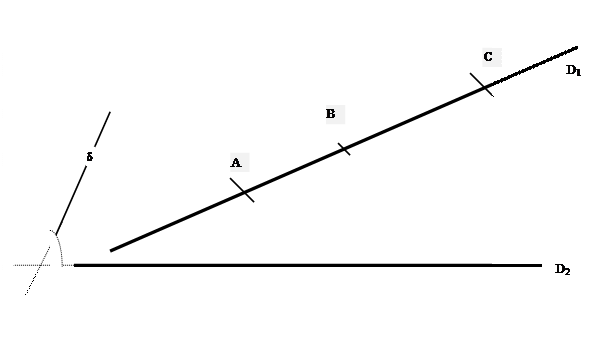
Tracer :
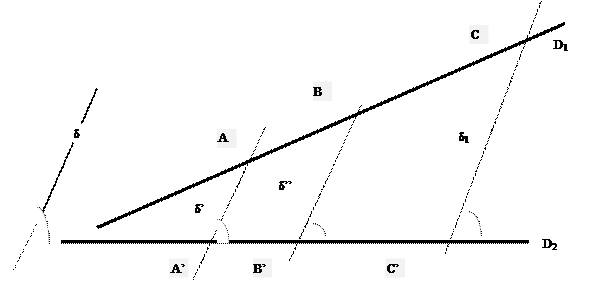
« La projection d’une division
irrégulière est une division irrégulière »
On trace des parallèles à « d »
passant par A ; B ; C et coupant D2 en A’ ; B’ ; C’ ;
CAS
d’une division régulière d’un
segment :
La longueur du segment AB
est égale à la longueur du segment BC
est égale à la longueur de CE
Données : la droite D1 est graduée régulièrement ,la droite « d »
est la direction , D2 est la droite à diviser « régulièrement » en
trois parties égales.
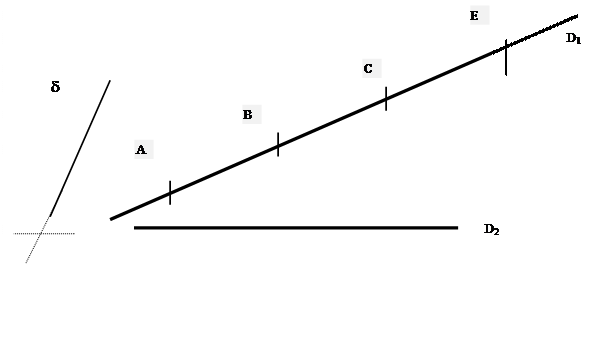
La longueur du segment A’B’ est égale à
la longueur du segment B’C’ est égale à la longueur de C’E’ :
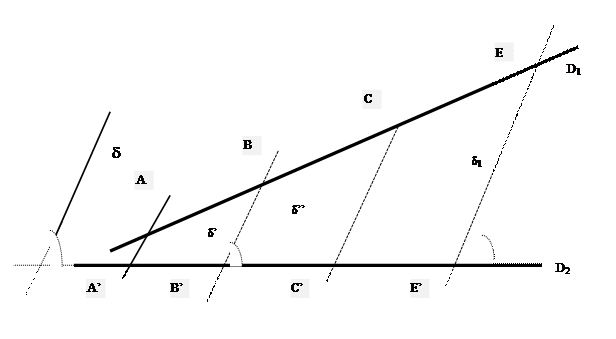
Par
projection nous obtenons les points A’ , B’ ; C’ ; E’
Nous pouvons remarquer
que la longueur du segment A’B’ est égale à la longueur du segment B’C’ est égale à la
longueur de C’E’ :
en
conclusion : « La projection
d’une division régulière est une division régulière »
Pour diviser régulièrement une droite bornée à partir
d ’une droite régulièrement divisée nous
appliquerons le théorème suivant :
L’image ,
dans une projection régulière est une division régulière.
Autre
cas : les deux droites D1 et D2 sont sécantes (elles se coupent
,elles ont donc un point commun)
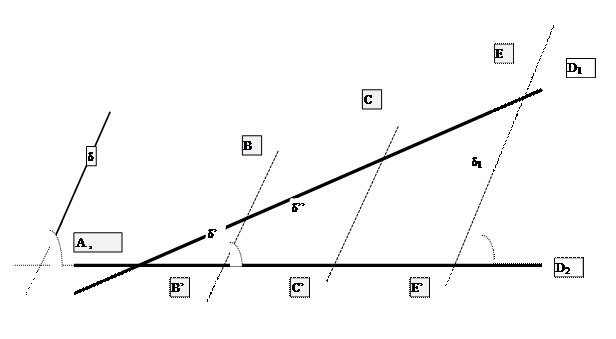
Les
points A et A’ sont confondus.
d’où le
théorème de THALES :
Plusieurs parallèles
déterminent sur 2 sécantes quelconques des segments correspondants
proportionnels.
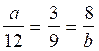 ;
;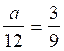
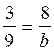
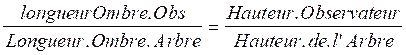
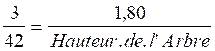 ;
;