Pré requis:

Les lignes
Le segment.
POINT LIGNE PLAN

ENVIRONNEMENT du dossier:

Index warmaths

Objectif précédent 1°) Fiche activités découvertes (6 ème collège) 2 °)Liste des figures géométriques élémentaires

Objectif suivant 1°) quadrilatères 2°) Tracés de polygones 3°) les polygones réguliers 4°) Les polygones irréguliers 5°) le périmètre d’un polygone irrégulier.

Liste des cours de géométrie. 1°) sommaire sur les polygones 2°) Info : Le périmètre des polygones

DOSSIER 1: LE POLYGONE 

	1. La ligne polygonale.
	2. Le polygone : définitions
	3. Angles d’un polygone « non » croisé.
	4. Convexité des domaines polygonaux.
	5. Définitions : irréguliers ou réguliers ; concaves ou convexes ;
	6. Classification des polygones usuels
TEST	COURS	Devoir Contrôle	Devoir évaluation	Interdisciplinarité 1° les polyèdres	Corrigé Contrôle	Corrigé évaluation
				2°) l’arpentage.

COURS

1° ) La ligne polygonale :
« consécutifs » Pré requis : deux segments sont dits « consécutifs » lorsqu’ils ont en commun une extrémité et qu’ils n’ont pas d’autre point commun. Exemple  Les segments [BA] et [AC] sont consécutifs , « A » est le point commun. Ils ont le même support de droite..
Une ligne polygonale est une suite de segments consécutifs , deux segments consécutifs n’ayant pas le même support.
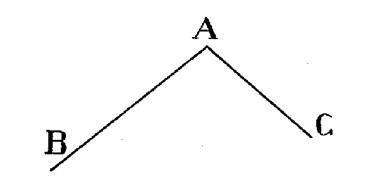
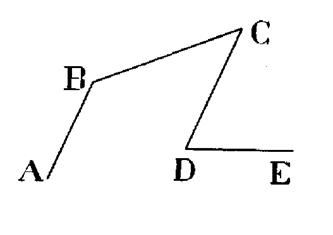
Ligne polygonale à deux segments…			Ligne polygonale à quatre segments
Les extrémités des segments sont les sommets de la ligne polygonale, et les segments en sont les côtés. On désigne aussi sous le nom de « côtés » les droites portant les segmens.
2°) Le polygone : définitions
Définition 1 d’un polygone :
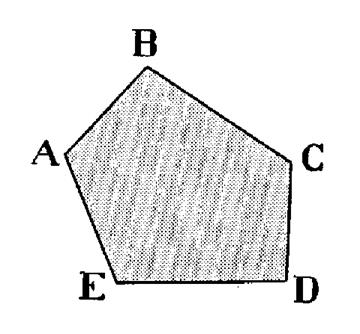
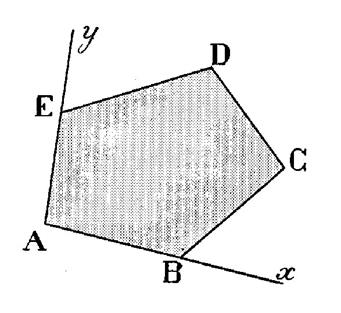
Un polygone est une portion de plan limitée par une ligne brisée fermée. · Les cotés de cette ligne sont les cotés du polygone. · Les points d'intersection de deux cotés consécutifs sont les sommets du polygone. · Les angles formés par deux cotés consécutifs sont les angles du polygone. ci-contre  : Polygone « ABCDE »
Définition 2 d’un polygone :
On appelle « polygone » la figure formée par : · Plusieurs points ( A B ; C ; D ; E ; ….)donnés dans un certain ordre et tels que trois points consécutifs ne soient pas sur la même droite. · Les segment sont déterminés chacun par deux points consécutifs , le premier point étant considéré comme consécutif du dernier .i Un polygone est donc une ligne polygonale fermée. Les points sont dits « sommets » et les segments sont dits « côtés ». On désigne aussi sous le nom de « côtés » les droites portant les segments.
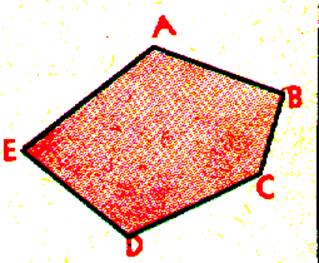
ci-dessus : Polygone « BCDEA »		Les segments joignant deux sommets non consécutifs sont les diagonales du polygone. On désigne sous le nom de diagonale ,les droites portant les segments. (exemple : CE)
3°) Domaine polygonal.
Un polygone peut limiter un domaine d’un seul tenant ; un tel domaine est dit : « domaine polygonal » Exemple :
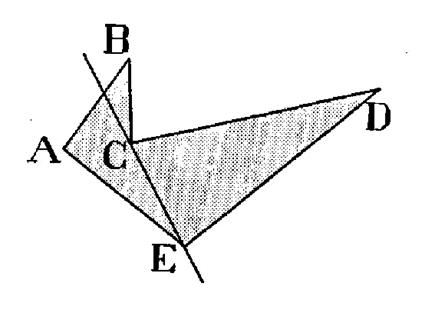
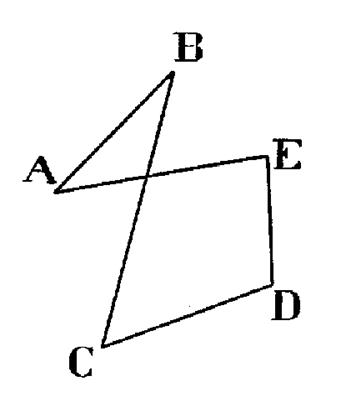
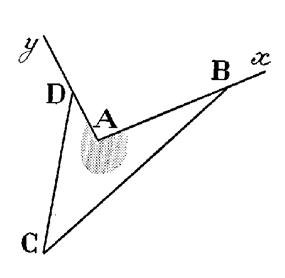
Dans le cas contraire , le polygone est croisé, ne limite pas un domaine polygonal , car deux « segments cotés » , au moins , se coupent : Exemple :
4°) Angles d’un polygone « non » croisé.
Chaque sommet d’un polygone est l’origine de deux demi-droites supportant chacune un côté de ce polygone. L’angle de ces demi-droites , qui contient la partie du domaine polygonal avoisinant le sommet, est dit « angle » intérieur du polygone.
Nota :
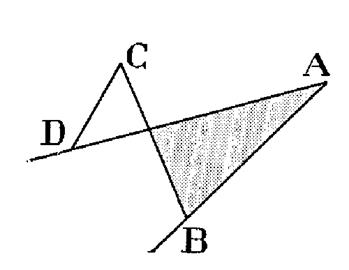
Lorsqu’ un polygone est croisé , la notion d’angle intérieur disparaît puisque le polygone ne limite pas un domaine . Cependant on peut choisir comme « angles » du polygone les angles convexes déterminés par les côtés . ( voir figure ci contre)
5°) Convexité des domaines polygonaux.
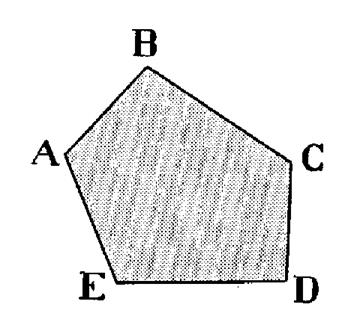
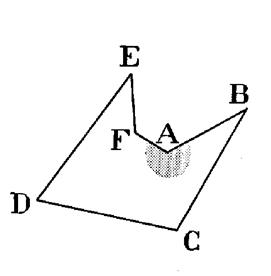
Soit un polygone non croisé « ABCDE » situé « tout entier » dans un des demi-plans déterminés par une quelconque des demi côtés. (voir figure ci-dessous). Le domaine polygonal « ABCDE » est la partie commune à cinq demi -plans ; ces demi – plans étant convexes , le domaine commun est convexe. Donc :
· Si un domaine polygonal est situé tout entier d’un même côté de chacune de ses droites – côtés , ce domaine est convexe. · Réciproquement , si un domaine polygonal est convexe , il est situé tout entier d’un même côté de chacune de ses droites côtés.
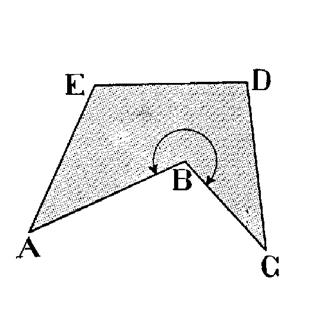
Evidemment , les angles intérieurs d’un polygone convexe sont convexes. Le domaine est d’ailleurs le domaine commun à tous les angles intérieurs. Voir la figure ci-dessous.			Si le domaine polygonal n’est pas convexe , il est dit « concave ». UN , au mons, de ses angles intérieurs est supérieur à « 180 ° » Voir figure ci-dessous.
Suivant le domaine polygonal est convexe ou concave le polygone est dit : « convexe » ou « concave ».
Un polygone peut-être « convexe » ou « concave » :
Remarque : un polygone peut-être « régulier » ou « irrégulier » ; les polygones « réguliers » sont des polygones « particuliers »
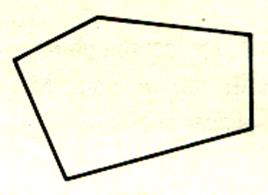
a) Le polygone convexe :
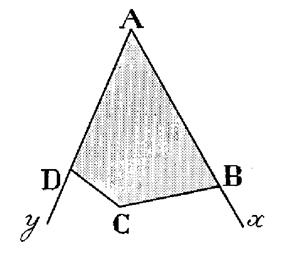
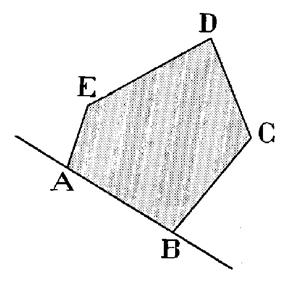
Le polygone convexe n’est pas coupé par le prolongement de l’un quelconque de ses côtés.
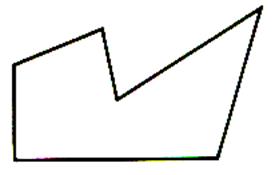
b) Le polygone concave
Le polygone concave est coupé par le prolongement de l’un ou plusieurs de ses côtés.
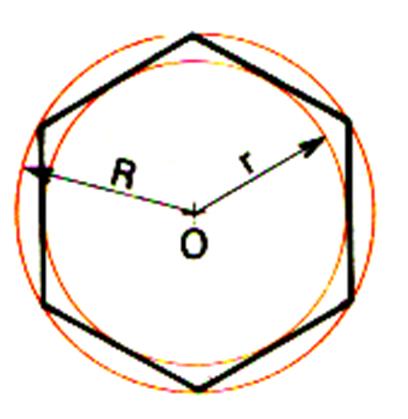
Remarque : Les polygones irréguliers sont souvent rencontrés dans les (@) opérations d’arpentages ( plan cadastral) C) Le polygone régulier : Il peut toujours être inscrit dans une circonférence ( O ,R) et circonscrit à une autre circonférence. ( O, r ) . Remarque : Il y a des polygones réguliers convexes et des polygones réguliers concaves ( dit :étoilés »)
a) Le polygone régulier convexe :
Le polygone régulier convexe n’est pas coupé par le prolongement de l’un quelconque de ses côtés. Il a ses angles et ses côtés égaux . Exemple :l’hexagone
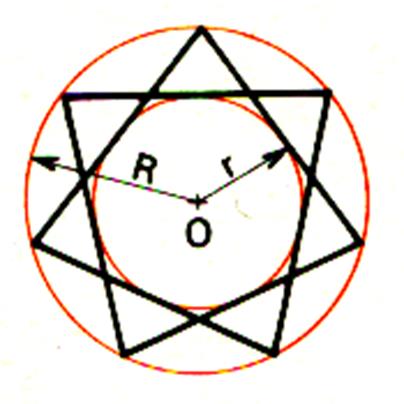
b) Le polygone régulier concave
Le polygone régulier concave est dit « étoilé » si la ligne fermée est obtenue en joignant les points de division non consécutifs )
6°) Classification des polygones usuels sont : En cliquant sur les mots vous avez accès à de plus amples informations sur la figure :

I ) Les polygones de 3 cotés
A 3 côtés : Les triangles
		1. Scalènes
		2. Rectangles
		3. isocèles
		4. équilatéraux
II )Les polygones de 4 cotés (Les quadrilatères)
		Polygones quelconques à quatre cotés
		Les parallélogrammes :
			1. Le rectangle
			2. Le carré
			3. Le losange
			4. Le trapèze
III ) Les polygones réguliers de plus de 4 cotés
	1. Le pentagone		(5 cotés)
	2. L’hexagone		(6 cotés)
	3. L’ heptagone		( 7 cotés)
	4. L’octogone		( 8 cotés)
	5. L’ennéagone		( 9 cotés)
	6. Le décagone		( 10 cotés)
	7. Le dodécagone		(12 côtés)
IV ) Les polygones irréguliers de plus de 4 cotés
V) Les polygones étoilés
VI ) Fractals

NOTA :Les principaux polygones réguliers sont :

Le triangle équilatéral	3 cotés
Le carré	4 cotés
Le pentagone régulier	5 cotés
L’hexagone régulier	6 cotés
L ‘ octogone régulier	8 cotés

Quant aux autres polygones réguliers , pour éviter l'emploi de termes techniques trop "prétentieux" , on les désigne par le nombre de leurs cotés.

Ainsi l'on dit : un polygone à 7 cotés , un polygone à 11 cotés , un polygone de 15 cotés,…etc.

Un triangle se désigne par trois lettres , un quadrilatère par quatre lettres , et un polygone quelconque par autant de lettres qu'il renferme d'angles.

Il y a dans un polygone autant d'angles qu'il y a de cotés.

TRAVAUX AUTO FORMATIFS.

CONTROLE :

1. Qu’est qu’un polygone concave et convexe?

2. Qu’est qu’un polygone régulier convexe et concave ?

3. Comment nomme –t-on les polygones à 3 et 4 côtés ?

EVALUATION

Série 1

Nommer les polygones de 5 cotés ou plus

5 cotés

6 cotés

7 cotés

8 cotés

9 cotés

10 cotés

Série 2

Combien de côtés ont les polygones suivants

Le décagone

L’hexagone

L’octogone

L’ heptagone

Le pentagone

L’ennéagone

Travaux :

Pré requis : @ Savoir utiliser le rapporteur.

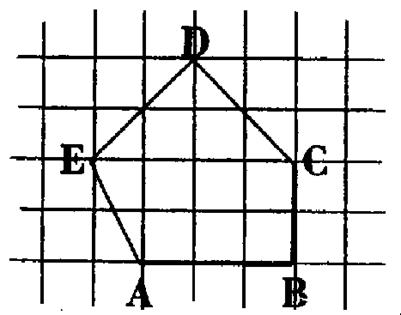
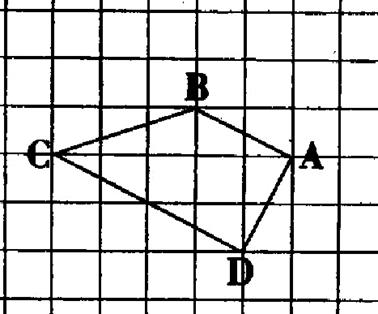
1°) Reproduire la figure ci-dessous .

· Mesurer les angles du polygone .Quelle est la somme de ces angles.

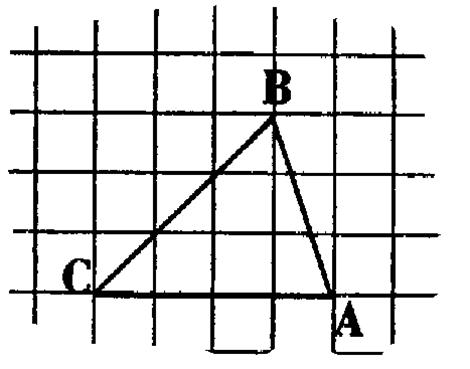
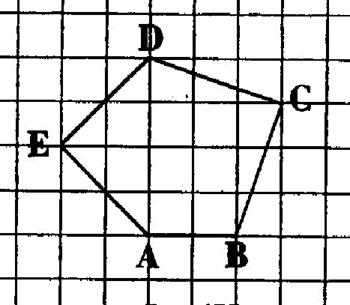
2°) Reproduire la figure ci-dessous .

· Mesurer les angles du polygone .Quelle est la somme de ces angles ? .

3°) Reproduire la figure ci-dessous .

· évaluer la somme de ces angles ? .

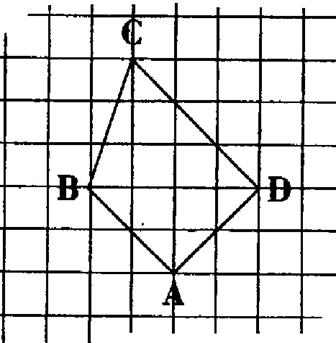
4°) Reproduire la figure ci-dessous .

· Mesurer les angles du quadrilatère .Quelle est la somme de ces angles ? .

5°) Faire la somme des angles du polygone

6°) Quelle est la nature du quadrilatère ?

Mesurer les angles du quadrilatère .Quelle est la somme de ces angles ? .

7°)Reproduire la figure . Combien y a t- il de carrés intérieurs au domaine limité par le polygone ?

ce nombre est l’aire du polygone.

8°) Reproduire la figure ci-dessous . Evaluer l’aire du polygone.

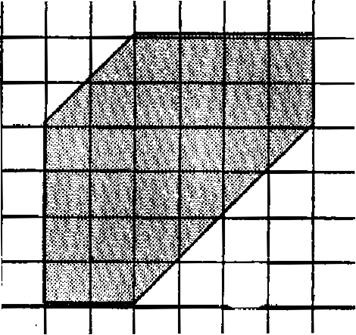
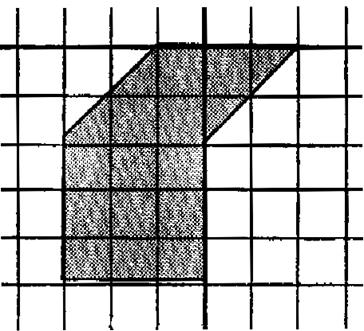
9°)Reproduire la figure ci-dessous .Le domaine grisé est-il limité par un polygone.

Evaluer l’aire de ce domaine.

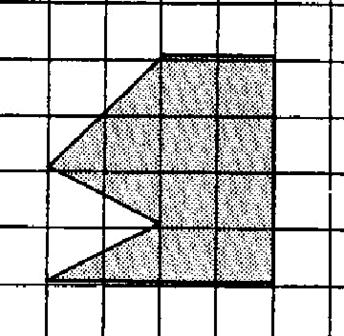
10°)Reproduire la figure ci-dessous .Le domaine grisé est-il limité par un polygone. Evaluer l’aire de ce domaine.

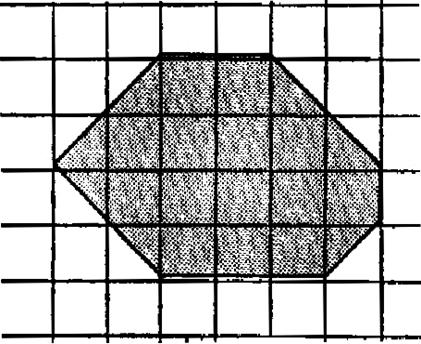
11°) Reproduire la figure ci-dessous .Le domaine grisé est-il limité par un polygone. Evaluer l’aire et le périmètre de ce domaine.

12°) Reproduire la figure ci-dessous .Le domaine grisé est-il limité par un polygone. Evaluer l’aire et le périmètre de ce domaine.

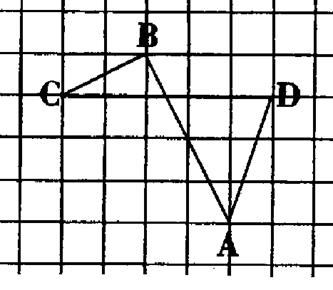
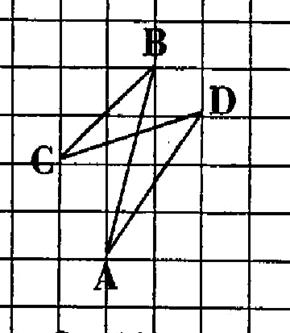
13°) Reproduire la figure ci-dessous . Quel est le périmètre du polygone ? le quadrilatère croisé limite - - il un domaine ?

14°) Reproduire la figure ci-dessous .Evaluer l’aire , le périmètre et la somme des angles intérieur du polygone.

15°) Reproduire la figure ci-dessous . Evaluer l’aire , le périmètre et la somme des angles intérieur du polygone.

INTERDISCIPLINARITE