Cet accroissement , qui peut – être positif , ou négatif , se désigne par « D x » ( ce groupe de deux lettres « delta et ixe » constitue un symbole unique , jouant le même rôle qu’une seule lettre ) de sorte que l’on a

D x = x₁ - x₀ ou x₁ = x₀ +D x

Soit « y » une fonction de « x » définie dans un certain intervalle ;

X₀ et x₁ sont deux valeurs de « x » appartenant à l’intervalle,

y₀ et y₁ sont les valeurs correspondantes de y .

Appelons accroissement de « y » correspondant à l’accroissement de « x » , la différence y₀ - y₁ = D y ;

en résumé :

Accroissement de x D x = x₁ - x₀ ; valeur finale de x Û x₁ = x₀ + D x

Accroissement de y D y = y₁ - y₀ ; valeur correspondante de y Û y₁ = y₀+D y

Exemple : soit la fonction y = 2 x² - 7 x + 5

1^er couple de valeurs : x₀ = 2 y₀ = 8 - 14 + 5 = = - 1

2^ème couple de valeurs : x ₁ = 2 + ∆ x y₁ = 2 (2 + ∆ x )² - 7 ( 2 + ∆ x ) + 5

soit y₁ = - 1 + ∆ x + 2 (∆ x ) ²

Les accroissements correspondants sont :

∆x et ∆ y = ∆ x + 2 (∆ x )²

Refaisons le même calcul sans préciser la valeur initiale :

1^er couple de valeurs : x ₀ ; y ₀ = 2 x₀² - 7 x ₀ + 5

2^ème couple de valeurs :

x ₁ = x ₀ + ∆ x

y ₁ = 2 ( x ₀ + ∆ x) ² - 7( x ₀ + ∆ x) + 5

= 2 x₀² - 7 x ₀ + 5 +( 4 x₀ - 7 x ₀ ) ∆ x + 2 (∆ x )²

Les accroissements correspondants sont : ∆ x et ∆ y = (4 x₀ - 7 x ₀) ∆ x + 2 (∆ x) ²

II ) Des limites : A propos des dérivées nous rencontrerons une notion importante : celle de « limite » qu’il nous faut définir .

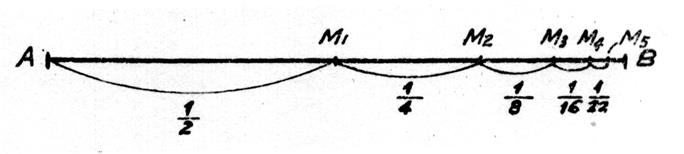
Considérons un segment de droite AB représentant l’unité :

Soit M₁ le milieu de AB , AM₁ représentant le milieu ,soit M₂ le milieu de M₁B , M₁ M₂ représente le quart ( ) , soit M₃ le milieu de M₂ B , M₂ M₃ représente le etc ; ….Soit M₄ le milieu de …..

limit

Il est évident que les points « M » successifs se rapprocheront constamment du point « B » mais ne l’atteindront jamais puisque chaque point « M » est le milieu d’un segment de droite ayant justement « B » comme extrémité.

Il en résulte que la somme :

S = ++ + +++ ……

Se rapproche constamment de l’unité lorsque le nombres de ses termes augmente indéfiniment , elle peut n’en différer que d’une quantité aussi petite que l’on voudra mais elle ne sera jamais rigoureusement égale à l’unité . On dit que « S » a pour limite 1 ou tend vers 1 lorsque le nombre de ses termes augmente indéfiniment .

Dans certains calculs on a à considérer plusieurs quantités u , v , w qui tendent respectivement vers des limites u₁ , v₁ , w₁ . Nous admettrons , sans le démontrer , que la somme u + v + w a pour limite u₁ + v₁ + w₁ , que le rapport a pour limite , que le produit u . v . w a pour limite u₁ . v₁ . w₁

III ) DEFINITION de la dérivée : ( info ++)

Exemple de calcul de la dérivée :

Considérons la fonction y = x² ( 1)

Si la variable « x » s’accroît d’une quantité très petite appelée (delta de « x » ) et noté : D x la variable devient x + D x .

La fonction « y » s’accroît d’une quantité correspondante D y et devient y + D y

Proposons nous de calculer D y en fonction de D x puis le rapport

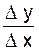
Appliquons la formule (1). Cette formule nous indique que la valeur de la fonction se calcule, en élevant au carré la valeur correspondante de la variable soit : y + D y = ( x + D x) ²

y + D y = x² + 2 x .D x + D x ² (développement : SOS )

supprimons y = x²dans les deux membres

D y = 2 x .D x + D x ²

le rapport s’obtient en divisant les deux membres par D x :

soit = 2 x + D x

On appelle dérivée de la fonction y = x² , par rapport à « x » , la valeur limite du rapport lorsque D x tend vers zéro. Il apparaît immédiatement que si D x s’évanouit tend vers 2x ;

« 2x » est la dérivée de « y » = x² par rapport à « x »

A) Définition: la dérivée d’une fonction est la limite , vers laquelle tend le rapport de l’accroissement de la fonction à l’ accroissement correspondant de la variable , lorsque celui-ci « s’évanouit »

Remarque :

Pour bien comprendre la nature de la dérivée il importe de remarquer que D x et D y s’annulant simultanément si D x = 0 , D y = 0 et le quotient prend la forme indéterminée qui ne signifie absolument rien . Lorsque , dans l’exemple précédent , nous posons cette dérivée égale à 2x ; Nous disons : si D x tend vers zéro , le rapport = 2x +D x tend vers 2x , donc si D x = 0 , = 2x . Nous faisons ce qu’on appelle une extrapolation par continuité ; c’est à dire que nous admettons comme rigoureusement vrai pour D x = 0 , ce qui est de plus en plus approché lorsque D x tend vers zéro. Ce raisonnement n’est évidemment possible que si le rapport ne change pas brusquement de valeur au dernier moment , c’est à dire à la condition qu’il y ait continuité.

B) NOTATION : (INFO pour savoir plus précisément )

Si la fonction d’une variable s’exprime par y = f(x) sa dérivée se représente par y ’ ou f ’(x) ( lire : i grec prime ou « eff » prime de « x » )

Dans certain cas , la valeur limite du rapport , lorsque D x s’évanouit , se symbolise par la notation dite notation différentielle .

Au départ , on devra considérer l’expression comme une simple notation et ne pas y voir un quotient .

Cependant dans les applications pratiques , elle pourra être considérée comme un quotient et voici comment .

La dérivée étant la limite du rapport lorsque D x et D y sont très petits le quotient est une valeur approchée de la dérivée y’ , d’autant plus approchée que D x et D y sont plus petits .

Dans les applications pratiques , en physique par exemple , on peut prendre comme valeur de la dérivée y’ cette valeur approchée ; dans ce cas , on peut considérer que est le quotient de deux valeurs dx et dy , très petites des accroissements D x et D y .

IV) Signification géométrique de la dérivée ;

Nombre dérivé :

Rappelons qu’on appelle « tangente à une courbe » au point « A », la position limite de la sécante « AM » quand le point « M » de la courbe se rapproche indéfiniment du point « A ».

D’une manière précise, dire que la droite « AT » est tangente, c’est à dire que l’angle « TAM » des droites « AT » et « AM » peut être rendu aussi petit que l’on veut, à condition de prendre « M » suffisamment voisin du point « A ».

Remarques :

1 - Pour les courbes que nous aurons à considérer, on obtient la même tangente , que « M » se rapproche de « A » d’un côté ou de l’autre.

2- Au voisinage d’un point ordinaire, la courbe est d’un même côté de sa tangente , elle « touche » sa tangente , au sens vulgaire du mot ; sur une petite longueur, courbe et tangente sont graphiquement confondues.

3- Il peut arriver que la courbe traverse sa tangente , on dit dans ce cas que le point est un point d’inflexion.

Cela étant , on considère une fonction y = f (x) ayant une dérivée et sa représentation graphique.

Par définition : on appelle « nombre dérivé » le coefficient angulaire de la tangente à la courbe représentative de la fonction y = f (x ) est , en chaque point , égal à la valeur correspondante de la dérivée.

Soit en effet :

► « x₀ » est une valeur quelconque de « x » ;

► « y ₀ » = f ( x₀) la valeur correspondante de « y » ;

► « x₁ = x₀ + ∆ x » est une deuxième valeur de « x » ;

► « y₁ = y ₀ + ∆ y la valeur correspondante de « y ».

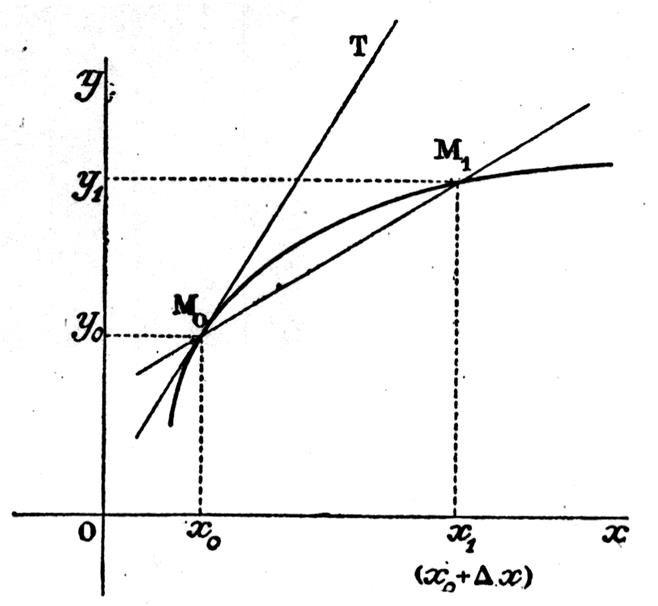
Soit M₀ et M₁ les points représentatifs.

Le coefficient angulaire de la droite M₀ et M₁ est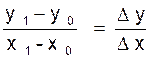

x₀ et y ₀ étant supposés invariables , et , par suite, le point M₀ fixe faisons tendre ∆x vers zéro ; ∆ y tend aussi vers zéro par hypothèse ; x₁ et y₁ tendent respectivement vers x₀ et y ₀ .

Donc :

1°) M₁ se rapproche de plus en plus de M ₀ et la droite M₀ et M₁ a pour limite la tangente « T » à la courbe.

2°) Le rapport a pour limite la valeur de la dérivée pour « x = x ₀ ». (voir la définition.

La tangente au point M₀ a donc pour coefficient angulaire la valeur « f ’(x₀) » de la dérivée en ce point.

tangente

Exemple de calcul :

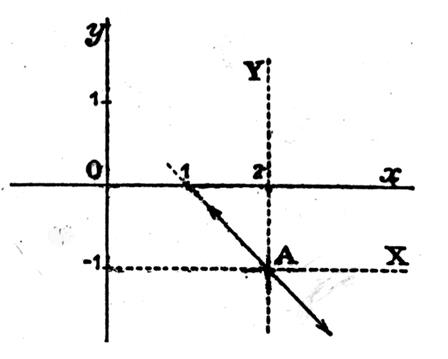
On donne y =

Calcul de la dérivée y’.

On sait que la dérivée de « a x² » est « 2ax »

La dérivée de y = est y’ = - soit y’=

Soit A le point d’abscisse « 2 »

Pour le point A :

« x = 2 » ; « y = - 1 » et «y’ = -1 »

Si nous menons par « A » les parallèles AX et AY aux axes de coordonnées : rapportée à ces nouveaux axes, la tangente en « A » est la droite d’équation « Y = - X »

pent

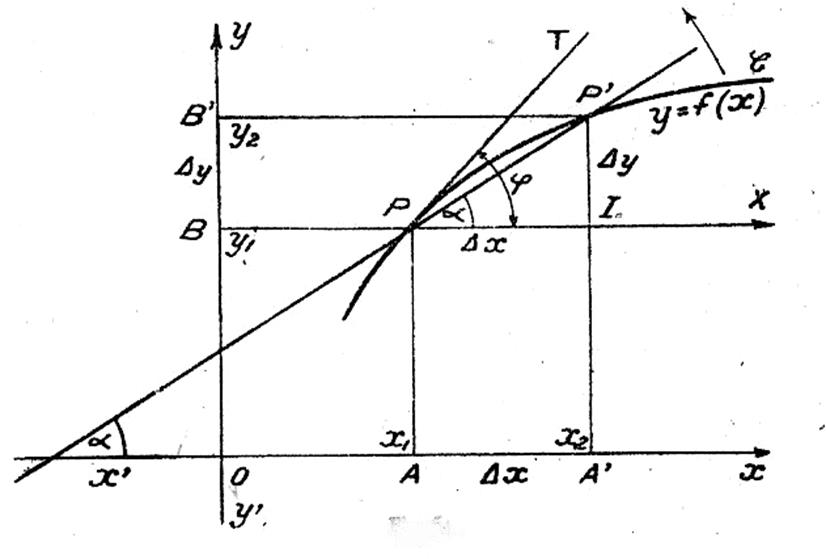
Complément d’informations : Sur la courbe « C » représentative de la fonction y = f(x) considérons deux points P et P’.

dér2

L’abscisse de P est = x₁ , son ordonnée = y₁

L’abscisse de P ’ est ’ = x₂ son ordonnée ’ = y₂

Désignons par Dx la différence des abscisses de ces points

D x = ’ - = ’

Pour Dy la différence de leurs ordonnées :

Dy = ’ - =

Dy représente l’accroissement de la fonction y = f(x) , lorsque la variable s’accroît de Dx à partir de x₁ . Traçons la droite PP’ , puis par le point P , la parallèle PX à la direction positive de l’axe des abscisses. Désignons par a l’angle que forme PP’ avec l’axe des abscisses ou avec sa parallèle PX , enfin menons au point « P » la tangente PT à la courbe C et désignons par j l’angle que forme PT avec l’axe des abscisses ou avec sa parallèle PX .

Dans le triangle PIP’ ; PI = Dx , ’ = Dy . Or , nous savons que dans un triangle rectangle , un côté de l’angle droit est égal au produit de l’autre côté de l’angle droit par la tangente trigonométrique de l’angle opposé au premier côté d’où

Dy = Dx tg a ; = tg a

Ainsi le rapport des deux accroissement mesure la tangente trigonométrique de l’angle a que forme la droite PP’ avec la direction positive de l’axe des abscisses , c’est à dire la pente de cette droite .

Voyons quelles sont les conséquences d’une réduction progressive de Dx

Si Dx diminue , le point P’ se rapproche de P le long de la courbe C et Dy diminue simultanément ; la droite PP’ tourne autour de P dans le sens de la flèche , l’angle a varie et nous avons constamment tg a ;

Si Dx s’évanouit , la sécante PP’ tend vers sa position limite qui est la tangente PT . Dy s’évanouit également et le rapport tend vers une valeur déterminée , qui est par définition la dérivée y’ .

L’angle a tend vers sa valeur limite j

La valeur limite du rapport mesure donc la tangente trigonométrique de la valeur limite de l’angle a

Autrement dit y’ = tgj

On voit donc que : la dérivée de la fonction y = f(x) pour x = x₁ , mesure la pente de la tangente menée à la courbe représentative de la fonction au point P , d’abscisse x₁

Exemple :

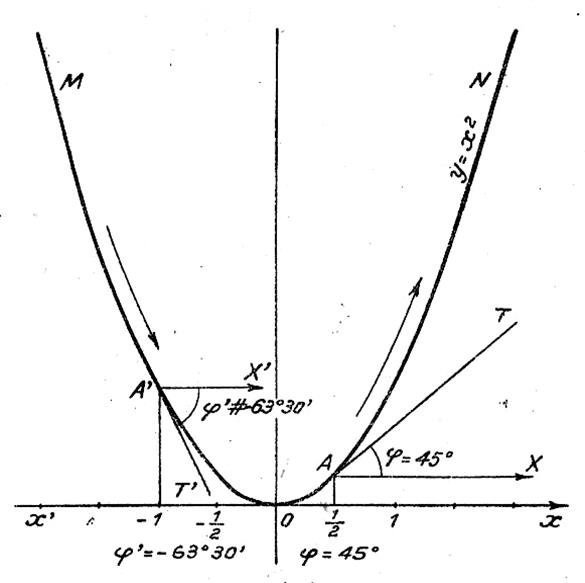
Sur une parabole d’équation y = x²

Considérons les points :

A et A’ d’abscisses + et –1

Traçons les tangentes AT et AT’ à la parabole , puis menons par A et A’ les parallèles AX et A’X’ à la direction positive de l’axe des abscisses.

La dérivée de y = x² étant

y ’ = 2x

Nous avons :

tg j = 2 = 1 ; j = 45°

tg j’ = 2 (-1) = -2 ;j’ ¹ - 63°30’

dér4

L’angle j est positif : la tangente AT est ascendante (montante ou croissante) , comme la portion de courbe à laquelle elle appartient ;

L’angle j est négatif, la tangente A’ T ’ est décroissante ( descendante), comme la portion de courbe à laquelle elle appartient.

V ) Signification cinématique de la dérivée :

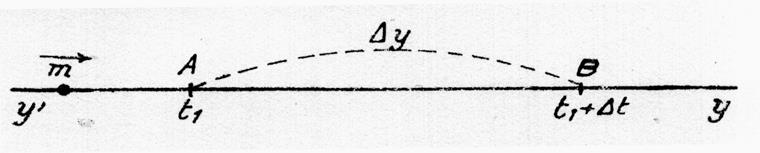
déri1

Imaginons un mobile « m » , animé d’un mouvement varié mais continu , d’équation y = f (t) ( lire :en fonction du temps) et parcourant la droite y’y .

Il passe au point A au temps t₁ et au point B au temps t₁ +Dt .

Si nous désignons par Dy la distance AB , le rapport mesure la vitesse moyenne du mobile entre A et B . Si nous réduisons de plus en plus l’intervalle de temps Dt , la longueur Dy décroît aussi de plus en plus , et le rapport tend vers une limite déterminée qui est la vitesse du mobile au point A ; or du point de vue mathématique , la valeur limite du rapport lorsque Dt s’évanouit est la dérivée de l’espace par rapport au temps dans laquelle on donne à « t » la valeur t₁ .

VI ) Signification « physique » de la dérivée.

D’une manière générale, la dérivée exprime une idée de variation instantanée, de vitesse.

Ainsi nous avons vu que pour un mouvement quelconque, la « vitesse » est la dérivée de l’espace e = f ( t) par rapport au temps.

On écrit :

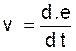
L’ « accélération » est la dérivée de la vitesse « v » = j ( t ) lire « par rapport au temps »

On écrit :

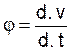
Autre signification :

- L’intensité ( I ) du courant électrique de décharge d’un condensateur est la dérivée de la quantité d’électricité en mouvement par rapport au temps.

On écrit :

- la force électromotrice (e) d’induction est proportionnelle à la vitesse de variation du flux, c’est à dire à la dérivée du flux par rapport au temps.

On écrit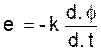

( « k » étant un coefficient qui dépend des unités choisies.)

VII ) Résumé (niv IV) :

Définition de la dérivée : soit une fonction y = f (x) définie et continue* dans un intervalle ( a ; b ) .

« x₀ » une valeur de la variable et « x₀ + ∆ x » une valeur voisine , appartenant toutes deux à l’intervalle ;

« y₀ » et « y₀ + ∆y » les valeurs correspondant de la fonction.

Nous formons le rapport :

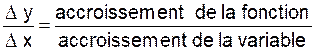
quand l’accroissement donné à « x » tend vers « 0 », l’accroissement résultant de ∆y tend aussi vers « 0 » (continuité) et le rapport précédent se présente sous la forme ( voir info +)

On appelle « dérivée de la fonction f (x) » pour la valeur « x₀ »de la variable, la limite ( si elle existe) du rapport de l’accroissement de la fonction à l’accroissement de la variable, quand ce dernier (∆ x) tend vers zéro.

On la désigne par y₀ ‘ = f ‘ ( x₀ )

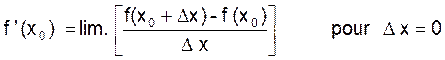
En général , à tout valeur « x₀ » d’un intervalle , correspond une valeur f‘ (x₀) de la dérivée.

La dérivée est donc une nouvelle fonction de « x » ; on la désigne y ‘ = f ‘ (x).

Exemple : y = f(x) = a x² ( « a » est un nombre donné)

1°) nous cherchons si cette fonction admet une dérivée pour x = -3.

- Calcul de « ∆ y » = f ( - 3 + ∆ x) - f (-3)

f (-3) = 9 a

f ( - 3 + ∆ x) = a ( - 3 + ∆ x)²

= 9 a - 6 a ∆ x + a (∆ x)²

donc ∆ y = (9 a - 6 a ∆ x + a (∆ x)² ) - ( 9 a )

soit ∆ y = - 6 a ∆ x + a (∆ x)²

- Calcul de

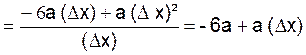
pour ∆ x = 0 , a pour limite « -6a »

« y = a x² » admet donc , pour « x= -3 » , une dérivée égale à : f ‘ ( - 3) = - 6a

Info : On dit aussi que le nombre dérivé est « -6a »

Lorsque l’on étudiera une fonction ; dans la représentation graphique de la courbe représentant cette fonction , on mettra en relation le nombre dérivé et le coefficient directeur de la tangente en un point donné de la courbe.

Recommençons le même calcul, avec la valeur « x₀ » de la variable.

f ( x₀) = a x ₀²

et f ( x₀+ ∆ x ) = a x ₀² + 2 a x ₀ (∆ x) + a (∆ x)²

donc ∆ y = 2 a x ₀ (∆ x) + a (∆ x)²

soit

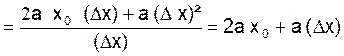
Pour ∆ x = 0 , a pour limite « 2 a x₀ »

Pour « y = a x² » admet donc , pour x₀ , une dérivée égale à f ‘ (x₀) = 2 a x₀

Remarque :

ce calcul montre que pour toute valeur x₀ de « x » , il existe une dérivée f ‘ ( x₀) = 2 a x₀ . En d’autres termes la dérivée de f (x) = a x² est une nouvelle fonction de « x » , f ‘ (x) = 2 a x

Revoir dans ce cours la signification géométrique de la dérivée.( chapitre IV)

*Information sur une « fonction continue » ou « continuité » :

Soit une fonction y = f(x) définie dans un intervalle donné ( a ; b) , on dit « qu’ elle est continue pour une valeur x ₀ de cet intervalle si elle a pour x ₀ une valeur bien déterminée f ( x₀) , et si , lorsque « x » tend vers « x ₀ » , sa limite est précisément f ( x₀). (voir cours sur les limites)

CONTROLE : aucun travail de prévu.

EVALUATION: