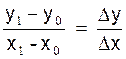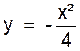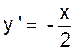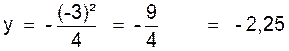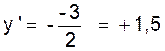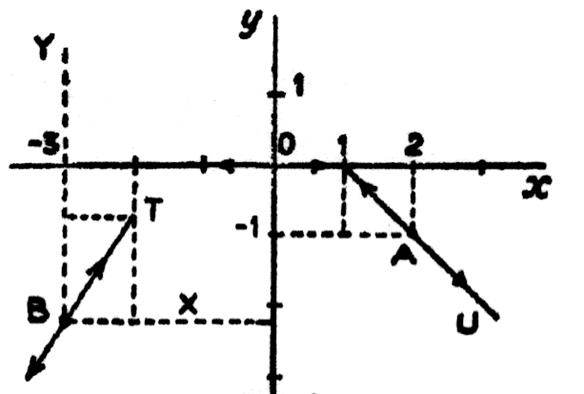|
|
|
|
Introduction à la notion de
« dérivée » et la définition de la dérivée. |
|
|
1°)Lecture : notions sur les dérivées 2°) Accroissements et notion de limite |
3°)Lecture pour d’autres explication……. 4°) « Le nombre dérivé » (
lien « tangente) 5°) Interprétation géométrique de la dérivée ( à venir) |
||
|
|
|
|
|
DERIVEE : Complément d’informations
sur la Signification
géométrique de la dérivée : « tangente » et suite…..« le nombre dérivé ».
|
Interdisciplinarité |
|
|
|
Tangente en un point d’une courbe : |
|
|
|
|
|
|
|
|
|
|
|
Travaux demandés sur le tracé d’une tangente en
un point : |
|
|
|
Construction de
tangentes à l’ aide de la dérivée : 1°) y = 2°) y =
x² ; y ‘ = 2x au point « x = 1 » 3°) y =
2x² ; y ‘ = 4 x au point « x = 0,5 » 4 °) y = - 0,3 x² ; y ‘ = - 0 ,6 x au point « x = 2 » ce travail permettra
de comprendre au cours de l’étude d’une fonction que par calcul de
la dérivée et l’analyse du signe ( +
ou - ) de cette dérivée , on peut déterminer
si celle ci est
« croissante » ou décroissante » dans un intervalle défini ,
et qu’un autre calcul partant de cette dérivée on pourra déterminer si il existe pour la fonction un
maxima ou un minima ainsi que sa valeur numérique . |
|
|
Signification
géométrique de la
dérivée ; |
|
|
|
|
|
|
|
|
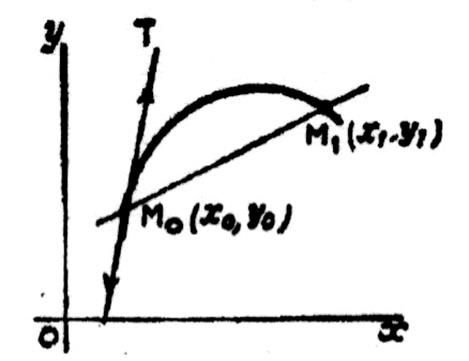
Soit le
théorème : le coefficient angulaire de la tangente à la courbe
représentative de la fonction « y = f (x) » est
, en chaque point , égal à la valeur
correspondante de la dérivée. |
|
|
Soit « x0 » une valeur de
« x » donnée et fixe ; la valeur correspondante de
« y » est « y0
= f ( x0) » ; elle est
également fixe. Soit M0 le point de coordonnées « x0 » ;
« y0 » ( point fixe) . Proposons nous de chercher le coefficient
angulaire de la tangente M0T en M0 à la courbe représentative . Pour cela, conformément à la définition de la
tangente à une courbe en un point,considérons , sur la courbe représentative,
un deuxième point M1 , variable, de coordonnées « x1 »
et « y1=f (x1)
( x1 et y 1 variables) et traçons la sécante M0M1. |
|
|
|
|
|
|
|
Sont coefficient angulaire ( ou
pente) est Coefficient angulaire de M0M1.
= Supposons maintenant que x1 tende vers
x0 ; y1 tende vers y0 ; Il en résulte que : 1°) d’une part , M1
tend vers M0 en suivant la courbe , et la sécante M0M1.
à pour limite la tangent M0T à la courbe. 2°)
d’autre part le rapport En conséquence, l’égalité (1) devient à la
limite :
Coefficient angulaire de M0T = f
‘ (x0) Nous avons bien démontré que la tangente au point
M0 a pour coefficient angulaire la valeur f ‘ (x0) de la dérivée en ce point. Application : Construction d’une tangente. Nous prenons la fonction Nous nous proposons de construire la tangente au
point « B » de coordonnées :
x = - 3 ;
donc pour x
= - 3 , on trouve |
|
|
Il est commode d’utiliser les axes
auxiliaires « BX » et
« BY » d’origine « B » , par rapport à ces axes , la
tangente en « B » a pour équation Y = 1,4 X ; si X = 1 on a Y = 1,5 , d’où le point
« T » ; la tangent « BT » |
|
|
|
|
|
|
|
Autres points : 1°) Pour « x = 0 » , on a « y = 0 » ,
« y ‘ = 0 »; c’est l’origine , la tangente est l’axe Ox. 2°) Pour « x = 2 » , on a « y = -
1 » et « y ‘ = -
1 » ; c’est le point « A » ; la tangente AU est parallèle à la deuxième bissectrice (
en axes pareillement gradués ; cette bissectrice concerne le deuxième et quatrième angle
droit du repère)). Il nous devient possible de calculer
l’équation de cette droite « tangente » en ce point : Par exemple cherchons l’équation de la tangente « BT »,
cette équation est de la forme : y = a x + b On connaît le coefficient angulaire ( =
1,5) « a = 1,5 ) d’où y = 1,5 x + b La tangent passe par « B » , donc
= - 2,25 = ( 1,5) ( -3) + b D’où « b = 4,5 - 2,25 = 2,25 » ; l’équation est
donc : y = 1,5 x + 2,25. Activité : rechercher l’équation de la tangente en
« A » . En utilisant la même
démarche. Et établir la procédure pour rechercher l’équation d’une tangente
en un point d’une droite d’équation donnée. Complément d’informations : Sur la courbe « C »
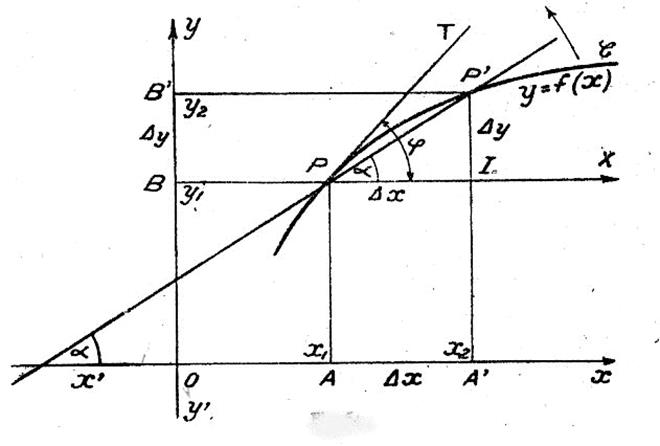
représentative de la fonction y = f(x) considérons deux points P et P’. |
|
|
|
|
|
|
|
|
|
L’abscisse de P est L’abscisse de P’ est Désignons par Dx la différence
des abscisses de ces points D x = Pour Dy la différence de leurs ordonnées : Dy = Dy représente
l’accroissement de la fonction y = f(x) , lorsque la
variable s’accroît de Dx à
partir de x1 . Traçons la droite PP’ ,
puis par le point P , la parallèle PX
à la direction positive de l’axe des abscisses. Désignons par a l’angle que forme PP’ avec l’axe des
abscisses ou avec sa parallèle PX , enfin menons au
point « P » la tangente PT à la courbe C et désignons par j
l’angle que forme PT avec l’axe des abscisses
ou avec sa parallèle PX . Dans le triangle PIP’ ; PI = Dx , Dy = Dx tg
a ; Ainsi le rapport des deux accroissement Voyons quelles sont les conséquences d’une réduction progressive de Dx Si Dx diminue ,
le point P’ se rapproche de P le long de la courbe C et Dy
diminue simultanément ; la droite PP’ tourne autour de P dans le sens de
la flèche , l’angle a varie et nous avons constamment tg a ;
Si Dx s’évanouit , la sécante PP’ tend vers sa
position limite qui est la tangente PT . Dy s’évanouit également et le rapport L’angle a tend vers sa valeur limite j La valeur limite du rapport Autrement dit y’ = tgj On voit donc que : la dérivée de la fonction y = f(x) pour x = x1 , mesure la
pente de la tangente menée à la courbe représentative de la fonction au point
P , d’abscisse x1 Exemple : |
|
|
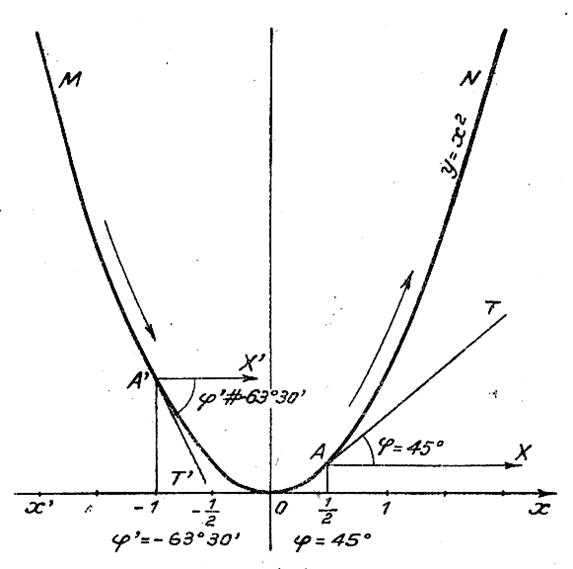
Sur une
parabole d’équation
y = x2 Considérons les points : A et A’
d’abscisses +
|
|
|
|
L’angle j est
positif : la tangente AT est ascendante (montante ou croissante) , comme la portion de courbe à laquelle elle
appartient ; L’angle j est
négatif, la tangente A’ T ’ est décroissante (
descendante), comme la portion de courbe à laquelle elle appartient. |
|
|
|
|
|
TRAVAUX AUTO FORMATIFS.
CONTROLE :
aucun travail de prévu.
Construire
les tangentes à l’ aide de la dérivée pour les fonction suivantes
, au point donnée ( sans avoir à tracer la courbe de cette fonction) .
1°) y
= ![]() au point « x =
-2 »
au point « x =
-2 »
2°) y
= x²
; y ‘ = 2x au point « x =
1 »
3°)
y = 2x² ; y ‘ = 4 x
au point « x = 0,5 »
4 °)
y = - 0,3 x² ; y ‘ = - 0 ,6
x au point « x = 2 »