calculs de dérivées

Par définition : On appelle « dérivée » de la fonction « y = f ( x) » pour la valeur « x₀ » de la variable la limite du rapport de l’accroissement de la fonction de l’accroissement de la variable , quand ce dernier tend vers zéro.

La procédure de calcul des dérivées découle de la définition

1►Donner à la variable un accroissement ∆x ;

2►Calculer l’accroissement correspondant ∆y ;

3►Ecrire la rapport et simplifier s’il y a lieu ;

4►Chercher la valeur limite de ce rapport quand ∆x s ‘ évanouit.

I ) Dérivée d’une constante. ( y = a)

La dérivée d’une constante est nulle car , par définition , une constante ne peut subir d’accroissement.

II ) Dérivée de y = a x

D’après la procédure :

y + (∆y) = a ( x + (∆x))

y + (∆y) = a x + a (∆x) (1)

Soustrayons y = a x aux deux membres de l’égalité (1).

(∆y) = a (∆x)

= a ; est a = constante

Le rapport est constamment égal à « a », il conserve cette valeur à la limite et y ‘ = a

On retiendra la règle : la dérivée de y = a x est y ’ = a

Exemples :

Soit y = 3 x ; y ‘ = 3

Soit y = x ; y ‘ = 1

Soit y = - x ; y ‘ = -1

Soit y = x ; y ‘ =

Info ---

III) Dérivée de y = x ⁿ

Info plus sur le binôme de newton.

En premier lieu , nous donnons la formule de Newton qui permet de calculer une puissance quelconque du binôme « a + b »

( a + b ) ⁿ = a ⁿ + + + + …….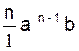

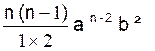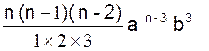Exemples :

1°) ( a + b ) ⁴ = a ⁴ + a ³ b + a ² b ² + 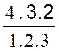a b ³ + 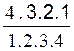a ⁰ b⁴

soit après simplification

( a + b ) ⁴ = a ⁴ + 4 a ³ b + 6 a ² b ² + 4 a b ³ + b⁴

2°) ( a - b ) ⁴ = a ⁴ - a ³ b + a ² b ² - 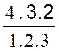a b ³ + 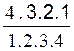a ⁰ b⁴

soit après simplification

( a + b ) ⁴ = a ⁴ - 4 a ³ b + 6 a ² b ² - 4 a b ³ + b⁴

On remarque qu’ il suffit dans le développement précédent ( 1°) , de changer le signe des termes contenant une puissance impaire de « b ».

Calcul de la dérivée de y = x ⁿ :

Appliquons la règle y + ∆y = ( x + ∆x ) ⁿ

Développement le second membre de l’égalité :

y + ∆y = x ⁿ +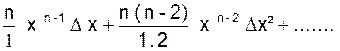

Soustrayons aux deux membres y = x ⁿ

∆y =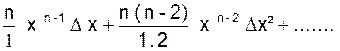

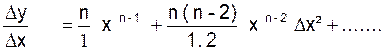
Si ∆x s’ évanouit : on considère que devient « y ‘ » et tous les termes contenant le facteur « ∆x » s’évanouissent en même temps que « ∆x » le second membre se réduit au terme « n x ^{n - 1} »

Ainsi « y ‘ = n x ^{n - 1} »

D’où la règle : la dérivée de y = x ⁿ est y ’ = n x ^{n - 1}

Exemples :

y = x² ; y’ = 2 x ^{2 - 1} soit y ‘ = 2 x

y = x³ ; y’ = 3 x ^{3 - 1} soit y ‘ = 3 x ²

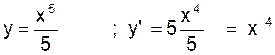
L’application de la règle précédente aux puissances à exposant négatif ou à exposant fractionnaire permet d’obtenir les dérivées des expressions de la forme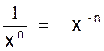

et des racines :

Exemples :

A ) puissances à exposant négatif :

1°) 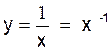; y’ = - 1 x ^{-1 -1} = - x ^-2 =

2°) 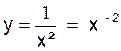; y’ = - 2 x ^{- 2 -1} = -2 x ^-3 =

Ainsi plus généralement :

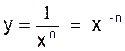; y’ = - n x ^{- n -1} = -n x ^{- (n + 1)} =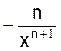

d’où la règle :

La dérivée de 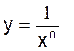est y ’ =

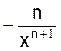
B ) dérivée des puissances à exposant fractionnaire

1°) y = ;

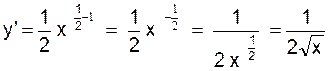
2°) y = ;

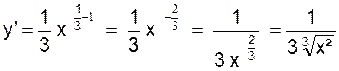
Plus généralement :

3°) y = ;

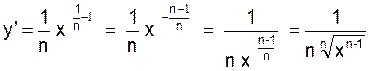
Règle : la dérivée de y = est

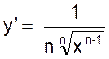
C) Dérivée d’une somme de fonction de même variable :

Soit y = u + v + w ; u ; v ; w étant des fonctions de « x ».

Nous donnons à « x » un accroissement « ∆x » :

Dans ce cas :

► « u » s’accroît de « ∆u » ;

► « v » s’accroît de « ∆v » ;

► « w» s’accroît de « ∆w » ;

ce qui a pour conséquence que « y » s’accroît de « ∆y » ;

nous avons évidemment : « ∆y = ∆ u + ∆ v + ∆ w »

nous divisons les deux membres par « ∆x »

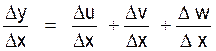
si « ∆x »

s’ évanouit tend vers « y ’ »

et 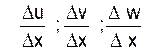tendent respectivement vers « u’ » , « v’ » , « w’ » dérivées de « u » , « v », « w »

A la limite , nous avons donc : y’ = u’ + v’ + w’

Règle : lorsqu’une fonction est la somme de plusieurs autres sa dérivée est la somme des dérivées de ces différentes fonctions.

D ) Application : Dérivée d’un polynôme entier . (info plus sur la dérivée de la forme « ax²+bx+c »)

Nous pouvons écrire maintenant la dérivée d’un polynôme quelconque entier en « x ».

Soit y = a x² + b x + c

Ce polynôme est la somme des trois termes. D’après la règle précédente il suffit de calculer les dérivées de ces rois termes et de les ajouter : la dérivée de « ax² » est « 2ax » ; la dérivée de « bx » est « b » ; la dérivée de « c » qui est une constante a une dérivée nulle d’où :

La dérivée de y = a x² + b x + c est y’ = 2ax + b

Exemples de dérivées de polynômes.

1 - y = 4 x ³ - 2 x² + 5 x - 1 a pour dérivée y’ = 12 x² - 4 x + 5

2 - y = - 25 x² + 12 x - 36 a pour dérivée y’ = x³ - 50 x + 12

3- y = r I ² + E I ( r et E sont des constantes) alors y’ = 2 r I + E

4 - y = 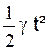( ﻻ est une constante) alors y’ = ﻻ t

TRAVAIL AUTO FORMATIFS.

CONTROLE : aucun travail de prévu.

Savoir énoncer les règles.

EVALUATION:

Il faut savoir refaire les exercices du cours.