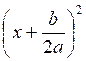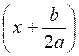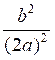les identitées remarquables (a + b) ²

Pré Requis:  

 

Définition "identité"

Boule verte

Les égalités   EG1             

Boule verte

Les égalités   EG2             

Boule verte

Développer

Boule verte

Les éléments et ensembles 

Boule verte

 

Environnement du cours :

 

INDEX       warmaths

Objectif précédent : 

 Liste des cours sur les identités remarquables   Sphère metallique

Objectif suivant

      Sphère metallique

INFO :  résumé   Sphère metallique

Ou  autre : Sphère metallique

 

Les    IDENTITES  REMARQUABLES  de la  forme  ( A + B )2

TEST

           FilesOfficeverte

COURS

                FilesOfficeverte

Devoir contrôle FilesOfficeverte

Devoir évaluation FilesOfficeverte

Interdisciplinarité

                        Filescrosoft Officeverte

 

Corrigé Contrôle  FilesOfficeverte

Corrigé évaluation  FilesOfficeverte

 

 

 

 

 

INTRODUCTION

 

 

Cet   objectif  aborde les égalités remarquables , appelé aussi  « identités remarquables »

 

 

Cet objectif à pour but  d’apprendre à reconnaître identifier et  utiliser des types particuliers d’égalités  en vue de traiter rapidement l’analyse sur les polynômes du second degré.

 

 

 

 

COURS

 

 

Se souvenir que :

  (A + B ) 2   =  A2 +2AB  +B 2

 

Le travail qui sera demandé est de :

Savoir passer de la forme factorisée :

"(A + B ) 2 " à la forme développée  " A2 +2AB  +B 2 "

 

Ou  Savoir passer de la forme développer  " A2 +2AB  +B 2"

     à la forme factorisée "(A + B ) 2 "

          Développement de    ( a +b ) (a + b)

soit la forme factorisée  (a + b ) 2   ;

     Recherche de la forme développée:

          ( a +b ) (a + b),    on met un indice à « a » et « b »

ce qui donne :

         ( a1+b1 ) ( a2 + b2)  =  ?          se souvenir que   (a1  = a2   et     b1  = b2  )

 

                         aussi           a1 a2  + a1 b2 + b1 a2 + b1 b2    =    a 2 + ab +ab +b2    

 

(comme ab +ab est égal à 2ab )

Sos cours

 

on peut conclure que :

 

  (a + b ) 2   =  a2 +2ab +b2

Traduction en langage littéral : Le carré de la somme  de deux nombres est égal à la somme des carrées de ces nombres augmentés de leur double produit.

 

 

 

 

 

 

A ) Développer : ( x +1 ) ( x + 1 )  qui s’écrit   ( x + 1 ) 2

       

on applique : (a + b ) 2   =  a2 +2ab +b2

 

on pose a = x  et b = 1  ;

 

                                 (x + 1 ) 2   =  x2 +2 fois x fois 1 +12

On calcule pour chaque terme

2 fois x fois 1 = 2 x

12 = 1

 

                                   (x + 1 ) 2   =  x2 + 2 x +1

 

 

 

B)Développer : ( 3x + 2 ) ( 3x + 2 ) qui s’écrit   ( 3x + 2 ) 2  

 

on applique : (a + b ) 2   =  a2 +2ab +b2

 

On pose a  = 3x  et b = 2

 

: (3x + 2 ) 2   =  (3x)2 +2 fois 3x fois 2  +22

 

On calcule pour chaque terme:

(3x)2  = 9 x2

2 fois 3x fois 2 = 12 x

22  = 4

    Conclusion: (3x + 2 ) 2   = 9 x2 + 12 x + 4

 

 

Le résultat  de l’exercice suivant sera repris dans le second degré

Boule verte

 

 

Développer

 

 

 

=

 

On développe

xx +  +  +

 

On regroupe les termes

x2+ 2 ( ) +

 

On calcule

1 °) calcul :

 2 ( )  = ==

2°) calcul :

+ ==

On regroupe :

=  x2+  +

 

Remarque : l’écriture   x2   + 

 

Ce travail est reprit dans  la résolution des équations du second degré.

Est  la première partie (x2 + ) de la factorisation de l’équation :

ax2 + b x + c = a (x2 + + )

 

 

 

Factoriser

 

 

Factoriser : a2 +2ab +b2

Nous savons que la forme a2 +2ab +b2 est la forme développer de   (a + b ) 2  ; nous pouvons conclure que la forme factoriser de   a2 +2ab +b2   est   (a + b ) 2  .

 

Exercice type :

 

Factoriser:           9 x2 + 12 x + 4

 

Procédure: (de factorisation)

 

a )  On reconnaît un polynôme du second degré   (grâce au «  x2 » )

b)   Ce polynôme  contient trois termes positifs  il pourrait  être de la forme   a2 +2ab +b2

 

c) Nous allons comparer terme à terme ,pour vérifier si ce polynôme  peut se mettre sous la forme (a +b)2  ;    dont la  forme développée est   a2 +2ab +b2

 

 1 )   Est ce que   9 x2  est de la forme a2  ?

 

    9 est le carrée parfait de 3   on peut écrire  9x2 = 32 fois x2  ,

               ( se souvenir que le carré d’un produit est égale au produit des carrés (et inversement  le produit d’un carré est égal au carré des produits : 32x2  =( 3x )2    )

   

 on peut conclure que  9x2  est de la forme  a2  ;  soit ( 3x )2

 

2)   Est ce que  12x  est de la forme  2 a b ?

 

      on décompose 12 en produit de facteurs premiers : 12 = 2 fois 2 fois 3 ;   donc  12x s’écrit « 2 » fois « 2 » fois « 3 » fois « x »

   

     on en déduit que « ab »  vaut   « 2 » fois « 3 » fois « x »

 

     on sait que « a » vaudrait  3x    ;   reste  la valeur  « 2 »  pour « b »

 

 

3) Est ce que  « 2 » convient  pour « b »?   On sait que  b2 est égale à 4 ,que racine carrée de 4 vaut 2 ,   « b » à pour valeur  « 2 »

 

d) Inventaire des calculs:

   puisque a2  = ( 3x )2

  que  b  = 2  ;donc que b2 =4

  que  2ab  = 2 fois 3x fois 2 = 12x

e) Conclusion:

        9 x2 + 12 x + 4  est de la forme a2 +2ab +b2  ; avec a=3x et b=2

donc  la forme factorisée de  9x2 +12x +4  =  ( a + b ) 2

 

Réponse la factorisation de   9x2 +12x +4   est  (  3x  + 2 ) 2

 

Certains polynômes du second degré ne peuvent se factoriser avec cette méthode tels :

x2 + x + 1   ; x2+18x+77   ;  2x2+13x+21  ;........................

 

Nous trouverons une solution ,quand elle existe , d’opérer une factorisation lorsque nous aborderons  l’objectif traitant de l’équation du second degré. « EQUA2° »

 

APPLICATION

Données du problème :

Un rectangle a pour aire :  ........................

Sa longueur est de : x +

Sa largeur est de   x  +  ...

Questions  :

Calculer   « x »

Calculer sa longueur et sa largeur:

 

 

 

 

 

 

 

 

TRAVAUX AUTO FORMATIFS :

 

 

 

     CONTROLE:

 

Donner la forme mathématique du développer du carré d’une somme de deux nombres.

 

 

EVALUATION.

 

I )Développer:

 

(3x+1) 2 =

( x +1 ) 2 =

(x +3 )2

(x +)2=

(x +1) =

 

 

II ) Factoriser:

 

x2 +12x + 36    ;    16x2 + 4x + 9 ;

 

III )  Que faut-il ajouter aux expressions suivantes pour les transformer en carré d’une somme ?:

 

a2 + b 2 ; 9a2 + b2  ;a2 + 2ab ; 4a2 + 4ab ;  10ab + b2  ;  a2 + 9 b2