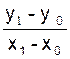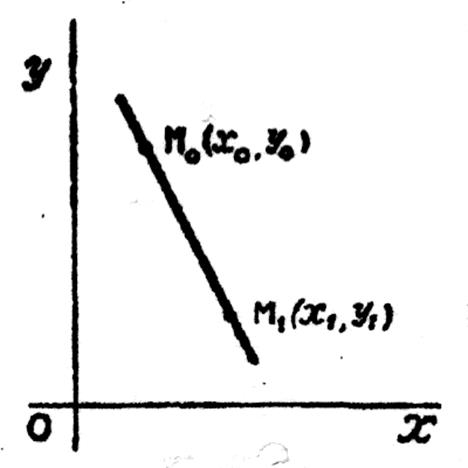Pré requis:
|
|
|
|
|
|
Index warmaths |
Objectif précédent : 1°) Coefficient directeur d’une droite. 2°) Ce qu’est la tangente en un point d’une courbe. |
1°)Les dérivées |
|
LA DERIVEE.
- Introduction
de la notion de dérivée. Problème des tangentes. (
Prépare à la définition de la dérivée)
-
Définition de la dérivée.
|
Interdisciplinarité |
|
Historique :
Le théorème qui va être
abordé donne le moyen de construire les tangentes à une courbe représentant une
équation de la forme « y = f(x) »
Ce théorème fournit ainsi
la solution générale du « problème des tangentes » auquel s’étaient
intéressés les mathématiciens français du XVII ème
siècle : Descartes ( 1596 - 1650) ; Fermat ,
Roberval.
Les dérivées ont été
inventées à peu prés
simultanément vers 1670 par Leibniz ( 1646-
1716) et Newton ( 1642 - 1727)
I
) Problème des tangentes.
On demande de chercher le coefficient angulaire de la tangente à une
courbe en un point donné.
|
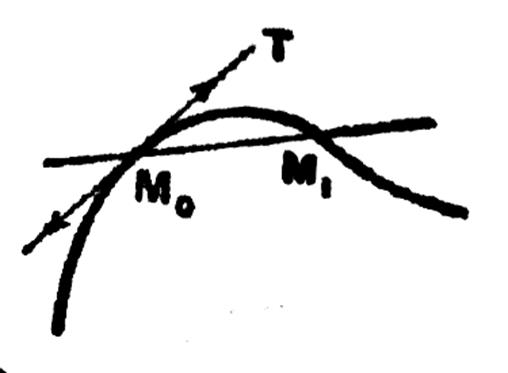
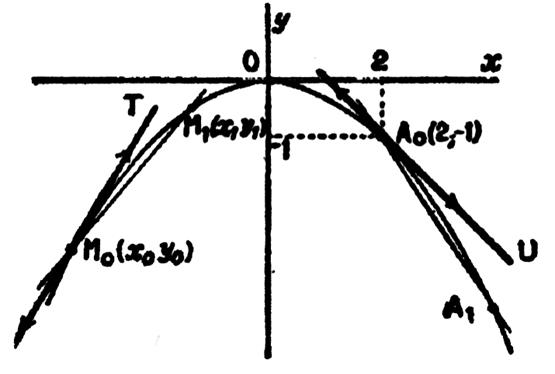
Rappel de la définition de la tangente en un
point :On appelle « tangente à une courbe
en un point M0 la position limite
M0 T de la sécante M0M1 quand le
point M1 de la courbe se rapproche indéfiniment du point M0 |
|
Exemple premier :
|
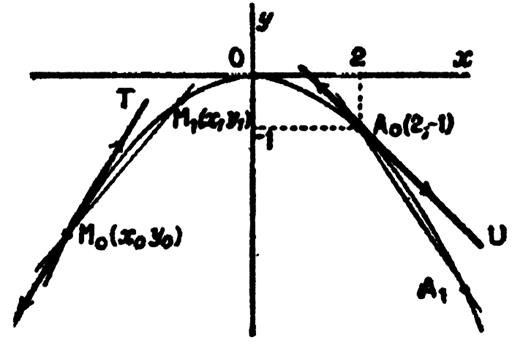
Soit la fonction y = Nous nous proposons de rechercher par le calcul
le coefficient angulaire de la tangente passant par un point « A0 » de droite « U » ; que l’on
note « A0 U » . ►Prenons sur la courbe un point « A1 » voisin du
point « A0 » |
|
Les coordonnées du point A0 sont « x 0» et
« y0 » ;
A partir de l’équation de la courbe y = ![]() ; on va se donner
les coordonnées du point A1 :
; on va se donner
les coordonnées du point A1 :
►
l’abscisse « x1 » est déterminée en écrivant que « x1 = x + ∆x » (1)
►
l’ordonnée « y1 » est obtenue par le calcul y1
= 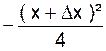 (2)
(2)
Application : On
veut connaître de la tangente passant
par un point ( A0)
Considérons ,
sur le graphique , le point « A0 » de
coordonnées x0 = 2 et y 0 = -1 (« y0 »
est obtenue par calcul et cette valeur
est vérifiée sur le tracé)
Nous pouvons trouver les coordonnées d’un point
« prés proche de A0
appelé « A1 » :
D’après (1)
: « x1 » = 2 + ∆x
D’après
(2) : l’ordonnée « y1 »
est obtenue en posant
l’opération : y1 = 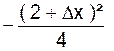
Le coefficient angulaire de la droite sécante passant par A0A1 est :
( d’après le calcul vu en
troisième) :
|
Rappel : le coefficient
angulaire d’une droite passant par deux points A0 (x0 ;
y0) et A1 (x1 ;
y1) est égal au calcul :
( cela correspond au calcul de la tangente…….) |
|
Fin du rappel.
Suite de
l’exemple premier : D’où :
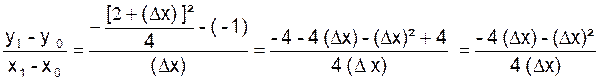
ou ,
en simplifiant par (∆x) , qui n’est pas nul :
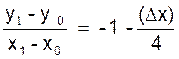 (
3)
(
3)
Supposons maintenant que (∆x)
tende vers « zéro » :
1°) x1 et y 1
tendent vers pour « x1 » :
2 et pour « y1 » :
-1 ; qui sont les coordonnées de « A0 » ;le point « A1 »
tend vers le point « A0 » en
suivant la courbe ; ainsi la droite A0A1 « sécante » tend vers la tangente
« A0U »
2°) le coefficient angulaire (3) de la « sécante » A0 A1 tend vers « - 1 ». La tangente A0
U a
donc pour coefficient angulaire « -1 » .
On dit que « -1 » est la dérivée de la fonction « y » = ![]() pour la valeur
« x0 » = 2
pour la valeur
« x0 » = 2
·« dériver » :
En tentant de rapprocher les points de la sécante A0A1
(au point de vouloir les superposer) , on « dérive » c’est à
dire que l’ on oblige la sécante à
passer en un point (double) de la
courbe ; cette sécante tend à devenir la tangente en un point . ( introduction à la notion de limite)
|
Nous partons de la même fonction et cherchons le
coefficient angulaire de la
tangente « M0
T » au point M0 de
coordonnées « x0 » et
y0 = |
|
Pour cela , prenons sur la
courbe un point voisin « M1 »
de coordonnées « x1 » et y1
= ![]()
Le coefficient angulaire de la sécante M0M1 est
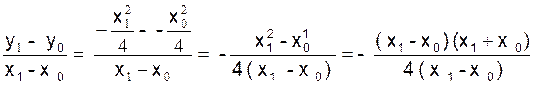
ou
en simplifiant par x1 - x 0
qui n’est pas nul :
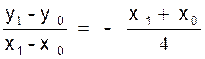 (1)
(1)
( Il
est plus commode , ici , d’utiliser « x1 » et non « x0 + ∆x », employé
dans l’exemple 1 précédent.)
Supposons maintenant que « x1 »
tende vers « x0 » :
1°) y1 ( = ![]() ) tend vers y0 ( =
) tend vers y0 ( = ![]() ) ; M1
tend vers M0 en suivant la courbe ; la sécante M0M1 tend vers la tangente « M0
T »
) ; M1
tend vers M0 en suivant la courbe ; la sécante M0M1 tend vers la tangente « M0
T »
2°) le coefficient angulaire ( 1) 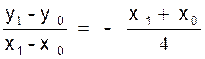 de la
sécante M0M1 tend
vers
de la
sécante M0M1 tend
vers 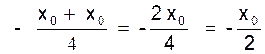
La tangente « M0 T » a donc pour coefficient angulaire ![]()
On dit que « ![]() » est la dérivée
de y =
» est la dérivée
de y = ![]() pour la valeur
« x0 »
pour la valeur
« x0 »
Remarques au sujet des fonctions
simples étudiées dans ce cours (niv
IV).
Soit y = f
(x) une de ces fonctions
, x0 une valeur de « x » pour laquelle elle
est définie.
1°) Lorsque « x » ,
tend vers « x0 » il
s’ensuit que y1 tend vers y0 autrement dit
, lorsque ∆x tend vers zéro , il s‘ensuit que l’accroissement
correspondant ∆ y tend
aussi vers zéro.
On dit que
la fonction « y » est continue pour x = x
0
2°) Lorsque ∆x tend vers zéro , et que , par conséquent, ∆ y tend aussi vers zéro , le rapport ![]() tend vers une
limite.
tend vers une
limite.
Nous venons de voir, sur deux exemples, que cette
limite s’appelle dérivée de y = f (x)
Soit une fonction y = f (x) définie dans un certain intervalle ;
« x0 » une valeur fixe de la variable , et x1 = x0 + ∆ x une autre valeur, appartenant toutes deux à
l’intervalle ;
y
0 et y 1 les
valeurs correspondantes de la fonction.
Calculons ∆ y = y 1 - y 0 les valeurs correspondantes de la fonction
et formons le rapport :
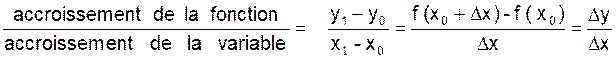
On appelle « dérivée » de la fonction
« y = f ( x) pour la valeur « x0 »
de la variable la limite du rapport ![]() de l’accroissement de
la fonction de l’accroissement de la variable , quand ce dernier tend vers
zéro.
de l’accroissement de
la fonction de l’accroissement de la variable , quand ce dernier tend vers
zéro.
On la
désigne par :
f ‘ ( x0 ) ou y
‘ 0
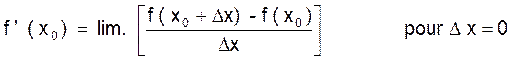
Ou
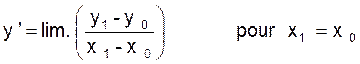
Attention à bien respecter l’ordre « x0 »
est toujours de valeur inférieure à « x1 » ; ce qui
n’est pas toujours le cas pour « y1 » et « y0 » ;
l’un ou l’autre peut avoir une valeur plus ou moins grande.
Rien n’est prévu
en contrôle et évaluation.