|
DOSSIER : LES
DECIMAUX non - relatifs / objectif cours 1 |
|
|
|
Pré requis: |
|
|
|
Revoir ce qu' est Le nombre décimal |
||
|
TRAVAUX PRE
REQUIS : avec les nombres entiers : |
|
|
|
|
||
|
|
||
|
|
||
|
|
|
|
ENVIRONNEMENT du
dossier:
|
Objectif
précédent : |
Objectif suivant
|
||
|
|
|||
DOSSIER
« calcul numérique »
ADDITION de deux nombres
décimaux positifs
|
COURS
|
Interdisciplinarité |
|
|||||
|
|
|
|
|
TRAVAUX : niv VI et V |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ACTIVITES :
Activités 1 :
|
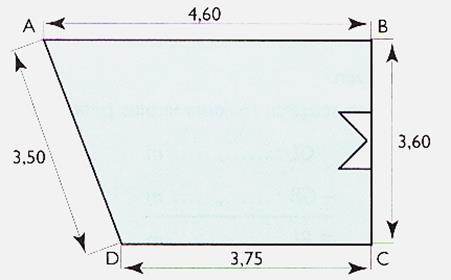
On donne ci contre un
dessin d’une pièce d’une maison ( dimensions en m).
Les points A ; B ; C ; D correspondent aux coins de la
pièce : AB est la longueur du mur entre le coin d’angle A et le coin
d’angle B. On demande de calculer le périmètre ABCD de cette
pièce . |
|
|
|
On pose l’opération suivante |
|
|
4 , 60 + 3 , 60 + 3 , 75 + 3 , 50 _________ 15 , 45 |
|
|
vérification |
|
|
3 , 50 + 3 , 75 + 3 , 60 + 4 , 60 _________ 15 , 45 |
|
Lorsque l’on pose une
addition en colonne ,
on doit veiller à ce que les chiffres de même rang soient alignés
dans la même colonne , ainsi que
les virgules.
Le
résultat d’une addition sera appelé : somme .
Activité 2 :
Lorsque l’on additionne des nombres
entiers et décimaux entre eux , on peut compléter les nombres
les plus courts par des 0 pour obtenir le même nombre de chiffres après la virgule , et pour les nombres entiers , mettre une
virgule et autant de zéro que le plus long nombres décimaux.
Exemple :
on va calculer 152 + 13,52 + 8 125,3 +
10 345,612 = ?
|
On va poser et effectuer l’opération en rajoutant les virgules et
zéros nécessaire , en prenant soin d’aligner les virgules |
1 5 2 , 0 0 0 + 1 3 , 5 2 0 + 8 1 2 5 , 3 0 0 + 1 0 3 4 5 , 6 1 2 __________________ 1 8 6 3 6 , 4 3 2 |
Activité 3 :
52,4 + 8,2 + 40 ,
55 = ……………et 8,2 + 40 , 55 + 52 ,4 =
…………..
Dans le calcul d’une somme , on peut changer l’ordre des termes ;
Calculer
2,5 + 3,18 + 1,5 en commençant par
effectuer 2,5 + 3,18 :……..
Calculer la même somme en commençant par effectuer 2,5 + 1,5 puis en ajoutant 3,18 : ……………..
Dans le
calcul d’une somme , on peut regrouper des termes pour
faciliter le calcul.
Exemple :
pour le calcul du périmètre de l’activité 1 :
On
effectue AB + BC
= 4,60 + 3,60 = 8,20
m =
ABC ( en m)
Puis on effectue : CD + DA = 3,75 + 3 ,50 = 7,25 m ( = CDA en m )
ABC + CDA = périmètre ABCDA = 8,20 m + 7,25
m = 15,45 m
ADDITION avec des nombres entiers naturels et des nombres Décimaux)
L’addition
est une opération : l’opération
simple de deux nombres est un calcul
qui consiste soit à
Additionner : c à
d ajouter des éléments à une somme
d’éléments existant .
Signe :
le signe indiquant que l’on doit faire une addition est « + » (attention à ne pas confondre ou
écrire cette croix : « ![]() » utiliser pour
indiquer que l’on doit effectuer une multiplication .
» utiliser pour
indiquer que l’on doit effectuer une multiplication .
Résultat
de l’addition : le
résultat de l’addition est appelé
« somme ».
Attention : On ne
sait faire que la somme de deux nombres.
exemple : 3,1 + 52,56 + 7 = ?
;(ce calcul n’a pas de résultat immédiat )
procédure pour
obtenir un résultat:
- prendre les deux premiers nombres et
faire leur somme :3,1 + 52,56 = 55,66
- remplacer 3,1 + 52,56 par 55,66
dans
l’opération de départ : 55,66 + 7
- faire le calcul : 55,66+ 7
= 62,66
Ordre
de grandeur d’une somme :
Toutes les fois que l’on doit faire une opération il faut estimer
mentalement un ordre de grandeur du
résultat afin d’éviter de grossières
erreurs lorsque l’on donnera le
résultat.
Cette
démarche est importante lorsque l’on prend la calculatrice ,
l’erreur de manipulation étant fréquente il faut ou vérifier (refaire le
calcul) ou estimer le résultat que l’on devrait trouver.
Pour cela il est important de savoir écrire et lire un nombre décimal
Rappels : (numération
du nombre décimal)
se souvenir qu
‘un nombre décimal comprend deux parties séparées par une virgule :
la
partie à gauche de la virgule se nomme « partie
entière »
la
partie à droite de la virgule s’appelle « partie décimale »
Lecture et utilisation du tableau :
par convention :
Les
traits verticaux déterminent des « colonnes »,entre
deux traits verticaux nous avons une colonne.
les traits horizontaux déterminent des lignes ;
entre deux traits horizontaux nous avons une ligne.
L ’ alignement horizontal des chiffres : 18403850 , 739 rangé dans le tableau suivant :
(placer la virgule et les chiffres de chaque coté situés de la virgule en conservant leur rang)
devient
le nombre décimal : 18 403 850 ,739 (remarquer l’espace entre
chaque classe),et il se lit : dix huit millions quatre cent trois mille huit cent
cinquante unités et sept cent trente neuf millièmes.
Ce
tableau doit aussi nous aider à placer
les nombres l’un en dessous de l’autre ,afin d’effectuer l’opération pratique.
utiliser le tableau suivant :
|
Partie
entière (multiples ) |
Partie
décimale (sous multiples) |
|||||||||||||||||
|
millions |
mille |
unités |
dixièmes |
centièmes |
millièmes |
|||||||||||||
|
cent aines |
dizaines |
unités |
cent aines |
dizaines |
unités |
cent aines |
dizaines |
unités |
0,1 |
ou |
1 /10 |
0,01 |
ou |
1/100 |
0,001 |
ou |
1/1000 |
|
|
|
1 |
8 |
4 |
0 |
3 |
8 |
5 |
0 |
|
7 |
|
|
3 |
|
|
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
FIN du RAPPEL

Pratique de l '
addition :
(Exploitation du tableau J)
Consigne : additionner : 2548, 58 + 78
592,043 =
Procédure :
a) Placer la
virgule du premier nombre sur le trait séparant la partie entière et la
partie décimale du premier nombre , ensuite
b) « entrer » les chiffres
. ( 8 ;4 ;5 ;2 ; ; ;5 ;8)
c) Placer la
virgule du premier nombre sur le trait séparant la partie entière et la
partie décimale du deuxième nombre , ensuite
d) « entrer » les chiffres (2 ;9 ;5 ;8 ;7 ; ; ; ;0 ;4 ;3 ;)
e) effectuer les additions par colonnes en commençant
par la colonne le plus à droite de la partie décimale.(ne
pas reporter « 1 »dans la colonne de gauche si la somme par colonne dépasse
« 9 ».
utiliser le
tableau suivant :
|
Partie
entière (multiples ) |
Partie
décimale (sous multiples) |
|||||||||||||||||
|
millions |
mille |
unités |
dixièmes |
centièmes |
millièmes |
|||||||||||||
|
cent aines |
dizaines |
unités |
cent aines |
dizaines |
unités |
cent aines |
dizaines |
unités |
0,1 |
ou |
1 /10 |
0,01 |
ou |
1/100 |
0,001 |
ou |
1/1000 |
|
|
|
|
|
|
|
2 |
5 |
4 |
8 |
|
5 |
|
|
8 |
|
|
0 |
|
|
|
|
|
|
+ |
7 |
8 |
5 |
9 |
2 |
|
0 |
|
|
4 |
|
|
3 |
|
|
|
|
|
|
= |
8 |
1 |
1 |
4 |
0 |
|
5 |
|
|
2 |
|
|
3 |
|
|
Ce qui donne le résultat : 8 1140 , 523
1° )Un marchand de nouveauté achète 2 pièces d’étoffe .La
première lui coûte 175,85 francs , la deuxième 195,25 francs ,de plus que la
première .Combien doit-il en tout ?
2° ) Un marchand de nouveauté
achète 2 pièces d’étoffe .La première lui coûte 175,85 francs , la deuxième
20,40 francs ,de plus que la première .Combien doit-il en tout ?
3°) Un marchand de nouveauté achète 3 pièces d’étoffe .La
première lui coûte 175,85 francs , la deuxième 20,40 francs ,de plus que la
première et la troisième autant que les deux premières ensemble .Combien
doit-il en tout ?
TRAVAUX AUTO FORMATIFS.
1.
Que signifie « additionner » ?
2.
Quel est le signe de l’addition ?
3.
Comment appelle - t on
le résultat de l ‘ addition ?
4.
Combien de parties compose le nombre décimal ?
5.
Nommer les parties qui composent
un nombre décimal.
6.
Construire le tableau de numération des nombres décimaux.
7.
Donner la procédure normale pour utiliser le tableau (le remplir) en vue de faire une addition de
deux nombres ?.
EXERCICES à faire sur
feuille ; vérification ensuite à la
calculatrice.
I ) Effectuer
les additions suivantes :
|
a |
167 +8 |
c |
753+ 6 |
d |
456+ 7 |
e |
830 +9 |
|
f |
256 +27 |
g |
485 +58 |
h |
849+ 95 |
i |
358 +24 |
|
j |
1 694+ 58 |
k |
3 274+43 |
l |
2 380+39 |
m |
8 764+73 |
|
n |
76 465+932 |
p |
46 178+375 |
q |
76 548+654 |
r |
56 381 +784 |
II ) Calculer:
|
a |
425+ 4 |
b |
237 + 5 |
|
c |
807 +46 |
d |
198 +27 |
|
e |
9 087+ 97 |
f |
2 783 +64 |
|
g |
54 639 +499 |
h |
98 569 +531 |
III )
Calculer:
|
a |
831+7 |
b |
217+ 4 |
|
c |
573 +81 |
d |
782+ 97 |
|
e |
6 781 + 21 |
f |
1470+18 |
|
g |
20 682 +702 |
h |
80 987 +614 |
IV ) Calculer
|
a |
630+ 3 |
b |
427 + 6 |
|
c |
632+ 19 |
d |
942 +72 |
|
e |
4 291+ 27 |
f |
5 431 +86 |
|
g |
56 045+ 792 |
h |
59 234 +321 |
AVEC
DES NOMBRES DECIMAUX :
I ) Effectuer les additions suivantes :
|
1 |
34,8+ 22 |
9 |
646 ,52+ 932 |
|
2 |
76,4+ 46 |
10 |
81 ,
786 + 373 |
|
3 |
39,7+ 19 |
11 |
638,19 +784 |
|
4 |
27,8+58 |
12 |
3 ,7654+ 845 |
|
5 |
288+ 2,1 |
13 |
7 211 +7, 81 |
|
6 |
627+ 5,6 |
14 |
4 560 + 67,5 |
|
7 |
798+ 3,7 |
15 |
4 001 +80,4 |
|
8 |
976+ 4,8 |
16 |
8 762+ 5,36 |
II ) (Suite)
|
1 |
62, 7 + 2,7 |
9 |
6 515,2 +4 ,14 |
|
2 |
6, 94 + 6,2 |
10 |
746 , 93+
47 ,1 |
|
3 |
31 ,2+ 2 ,3 |
11 |
5 ,7643+ 4 ,28 |
|
4 |
7 ,94+ 2,8 |
12 |
95 ,643 + 0 ,428 |
|
5 |
0 ,
985 +0, 39 |
13 |
|
|
6 |
5 ,61 +0 ,86 |
14 |
|
|
7 |
1 967 ,4 +7 , 55 |
15 |
|
|
8 |
48 ,
630 +4 ,87 |
16 |
|
III )
|
1 |
876 +300 |
9 |
0 ,
876 +3 , 200 |
|
2 |
504+ 450 |
10 |
2 +3 ,84 |
|
3 |
640 +800 |
11 |
9 ,
006 + 0 , 178 |
|
4 |
87 300 +4 000 |
12 |
1 ,
627 +0 , 0196 |
|
5 |
45 000 +6 050 |
13 |
|
|
6 |
70 800 +9 000 |
14 |
|
|
7 |
79 , 8+
720 |
15 |
|
|
8 |
6 ,
54 +3 000 |
16 |
|
Problèmes :
Avec son argent de poche , Franck s’achète un disque
à 9,95 € , une bande dessinée à 7,75F , un livre de poche à 1, 7 € et 3, 50 €
de bonbons . Il lui reste de quoi acheter une bande dessinée identique à
la première et 2 fois plus de bonbons qu’il n’en a mangé .
Quel était le montant de son argent de poche ?
Au marché , j’achète 0,840 kg de bœuf , 0,275
gr de jambon , 4,5 kg de fruits , un chou de 1,760g et 2,380 kg de carottes . Quelle charge
vais-je avoir à porter en revenant à la
maison ?