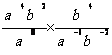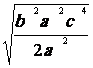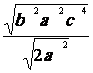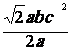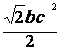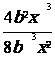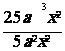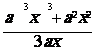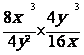Pré requis:
|
Mécanique (généralités) |
|
ENVIRONNEMENT du dossier:
AVANT :
|
APRES :
|
Complément d’Info :
|
PREPARATION CONCOURS niveau VI ;
V ; IV ; Résumé
des cours d’algèbre.
Travaux ;
devoirs
|
|
Corrigé
|
|||
|
|
Contrôle |
évaluation |
|||
COURS
N : ensemble des entiers naturels
N
= 0 ; 1 ; 2 ; 3 ; 4 ; 5 ; 6 ;……
Z : Ensemble des nombres entiers relatifs
Z
= ….. ( -3) ; (-2) ; ( -1) , 0 ; (
+1) ; (+2) ; (+3) ; …
D ±
Ensemble des décimaux relatifs
R : Ensemble des nombres
Réels ] - "‑ ; +"‑ [
@ L ‘ Ensemble des nombres réels
: R±
NOMBRE DECIMAL RELATIF :un nombre décimal non nul se compose d’un signe + ou
- , et d’un nombre décimal appelé valeur
absolue du nombre décimal relatif .
notation
=
4,25
= 4,25
Exemples de nombres décimaux relatifs
:
( -
4,8 ) nombre décimal relatif négatif
( +
4,8 ) nombre décimal relatif positif
LES
PROPRIETES des opérations dans D :
PROPRIETES DE L ‘ADDITION DANS « D± »
(
Info ++++)
-
Commutativité : a + b = b + a
-
Associativité ( a + b ) + c = a
+ ( b + c ) = a + b + c
-
Elément neutre : a + 0 = a
et 0 + a = a
PROPRIETES DE LA MULTIPLICATION DANS « D± »
-
Commutativité : a 
b = b a
-
Associativité ( a b ) c = a ( b c ) = a b c
-
Elément neutre : a 1 = a et 1 a = a
DISTRIBUTIVITE DE LA MULTIPLICATION PAR RAPPORT A
L’ADDITION :
-
a ( b
+ c ) = ab + a c
-
( a + b ) ( c + d ) = a c + ad + b c + bd
REGLES DE
SUPPRESSION DES PARENTHESES
1) Dans une suite d’additions et de soustractions , si une parenthèse est précédée du signe
plus :
-
on supprime la parenthèse
et le signe + qui la précède ;
-
on écrit alors les nombres
intérieurs à la parenthèse sans rien changer.
Exemple : 5 + [ (
-4,5) + 3,8 – 5 ] = 5 – 4,5 + 3,8 – 5
2) Dans une suite d’additions et de soustractions , si une parenthèse est précédée du signe
« - »
-
on supprime la parenthèse
et le signe « - » qui la
précède ;
-
on écrit alors les nombres
intérieurs à la parenthèse en changeant leur signe.
Exemple : 5 – [ ( -4,5) + 3,8 – 5 ] = 5
+ 4,5 - 3,8 + 5
2.1 Définition
Une puissance d’un nombre est le produit d’autant
de facteurs égaux à ce nombre qu’il y a d’unités dans l’exposant de la puissance .
Exemples : 2 4 = 2 222 = 16
Cas particuliers :
a 3 = a aa ; = a2a ; se lit :
a cube
a 2 = a a se lit : a carré
a 1 =
a l’exposant 1 ne
s’écrit pas , par convention
a 0 = 1
a1/2
= 
a1/3
= 
; etc…..
2.2 Puissance d’un nombre relatif .
« Toute puissance d’un nombre
positif est positive . »
exemples :
( + 4 ) 4 = ( + 4 ) ( + 4 ) ( + 4 ) ( + 4 ) = + 264
( + 2 )3 = ( +
2 ) ( + 2 ) ( + 2 ) = + 8
« Les
puissances d’un nombre négatif sont
positives si l’exposant est pair , négatives si
l’exposant est impaire »
exemples :
( - 4 ) 4 = ( -4 ) ( - 4 ) ( - 4 ) ( - 4 ) = + 264
( - 2 )3 = ( -
2 ) ( - 2 ) ( - 2 ) = - 8
2.3 Opérations sur les puissances d’un nombre relatif.
1) an a m = a n
+m
exemple : ( -4 ) 2 ( - 4 )5 = ( - 4 ) 7
( + 5
) ( +
5 ) 8 = ( + 5 ) 9
2) ( a m ) n = a mn
exemple [ ( - 4 ) 2]4 = (
-4 ) 8
3)
( a b
)n = a n b n
exemple :
[ ( -4 ) ( +2 ) ]4 = ( -
4)4 ( + 2)4
4)
n = 
exemple : 
3 =
5) 
= a –1 et
= a -n
exemples :
= a –3 ; 
= 2 –(-5) = 25
Note : écrire toujours des puissance positives .
Exemple : écrire 
et non a – 3
6) 
= a m-n
exemples : 
= a 2 ; 
= a –3 = 
Note sur les
puissances de 10 :
104 =
10 10 10 10 = 10 000
10n = 1
suivi de « n » zéro
10-n
= 0 , 000 ….01
( « n » chiffres derrière la virgule )
exemples : 10 9 = 1 000 000 000
10-9
= 0 ,
000 000 001
Exercices sur les puissances :
Simplifier les expressions suivantes :
|
|
|
|
|
|
|
[ (
- 7) 2]-3 = |
= ( -7) 2 |
|
|
|
|
= |
|
|
|
( a
b ) –2 = |
a-2
b-2 = |
|
|
|
( a2
b ) –4 = |
a2(-4) b (-4) = a-8
b-4 = |
|
|
|
( 2
a b –3 )-2 = |
2(-2) a (-2) b (-3)(-2) = |
|
|
|
|
|
|
|
|
|
|
|
5
3.1 Définition
la racine carrée d’un
nombre est un autre nombre dont le carré est égal au premier.
Exemple :
82 = 8 8 = 64
; 64 est le carré de 8 et 8 est
la racine carrée de 64
Notation : 
= 8
Par convention on écrit 
= 8 ; 
est appelé
« radical »
Note : le nombre sous le radical doit toujours
être supérieur ou égal à 0 :
impossible
remarques : 
= 0 ;
= 1
3.2 extraction
de la racine carrée. (voir cours)
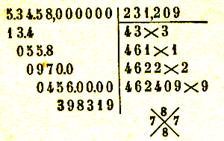
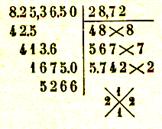
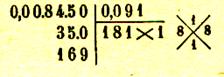
Extraction d’une racine carrée de nombres
décimaux :
Pour extraire la racine carrée d’un nombre décimal , on extrait d’abord la racine carrée de la
partie entière et on continue à abaisser
des tranches de deux chiffres décimaux , les tranches partant de la virgule
aussi bien pour la partie entière que
pour la partie décimale :
Exemples de calculs :
|
|
|
|
|
|
|
|
|
|
|
|
= 0,092 à 0,001 près
3.3 Propriétés :
1) 
= 
Exemples :
= 
= 
= 3 
= 30
= 
= 
= 3 
2) 
= 
Exemples :
= 
= 
= 
= 
= 
= 
3.4 Calcul sur les radicaux .
Exemples
2
+ 5+ 4 = 11
+ 
- 
= 
+ 
- 
= 2 
+ 5 - 4
= 3
la racine nième d’un nombre « a » est
un 2ème nombre « b » tel que bn = a
Notation :
= b
Exemples :
= 2 car 2 4 = 16
= 3 car
33 = 27 ( cette racine est
appelée « racine cubique » )
Exercices sur les racines :
1)
Calculer la racine carrée
de 78,48 à 
prés par défaut . ( 8,57)
2)
Mettre sous forme la plus
simple possible
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3) calculer : 5 
- 4 
+ 3 
+ 
= 5 
- 4 
+ 3 
+ 
=10 
- 24 + 9 + 5
= 0
4) simplifier : 
; 
|
|
|
|
|
|
|
|
|
|
5.1 – Définition
une fraction
est un symbole qui permet d’indiquer le résultat d’une mesure ou d’une
comparaison.
Notation :
Note : le dénominateur d’une fraction doit
toujours être différent de 0 .
5.2 Propriété fondamentale
lorsqu’on
multiplie ( ou divise) les 2 termes d’une fraction par un même nombre ( sauf
zéro ) , on obtient une fraction égale à la première .
Exemple : 
=
= 
= 
= 
= ….
Note : par convention ,
la fraction est notée
« 2 »
En généralisant : 
= a
5.3 Simplification .
Pour simplifier une fraction ,il suffit de diviser ses 2 termes par leur PGCD ; on obtient alors une fraction irréductible
égale à la fraction donnée .
Note sur le Plus Grand Commun Diviseur ( PGCD)
Le PGCD de plusieurs nombres est le plus grand des
nombres qui les divise tous exactement .
Pour trouver le PGCD de 2 ou plusieurs nombres , il suffit de :
-décomposer chaque nombre en produits de facteurs
premiers.
-faire le produit de facteurs communs affectés de
leurs plus petits exposants.
Exemple : recherche du PGCD de 18 ; 54 ; 126
|
|
|
|
|
54 |
2 |
|
126 |
2 |
|
|
18 |
2 |
27 |
3 |
63 |
3 |
||||
|
9 |
3 |
9 |
3 |
21 |
3 |
||||
|
3 |
3 |
3 |
3 |
7 |
7 |
||||
|
1 |
|
1 |
|
1 |
|
18 = 232 ; 54 = 2 33 ;
126 = 2 32 7
le PGCD = 232 =
18
Application aux fractions : rendre
irréductible 
|
|
225 |
3 |
|
525 |
3 |
|
75 |
3 |
175 |
5 |
||
|
25 |
5 |
35 |
5 |
||
|
5 |
5 |
7 |
7 |
||
|
1 |
|
1 |
|
225 = 32 52 ; 525 = 352 7
PGCD = 352 = 75
= 
= 
5.4
Réduction des fractions au même dénominateur
.
Pour réduire des fractions au même dénominateur .
Pour réduire des fractions au même dénominateur ,
il faut :
-
simplifier chaque
fraction s’il y a lieu ;
-
chercher le PPCM des
dénominateurs ;
-
multiplier les 2 termes de
chaque fraction par un coefficient convenable , de manière que le nouveau dénominateur soit
égal au PPCM.
Note sur le Plus Petit Commun Multiple ( PPCM)
Le PPCM de 2
ou plusieurs nombres est le plus petit nombre qui soit exactement divisible par les nombres donnés
.
Pour le déterminer , il faut :
-Décomposer chaque nombre en produits de facteurs premiers .
-Faire le produit de tous les facteurs différents
affectés de leur plus grand exposant .
Exemple : rechercher le PPCM de 84 et 90
Application aux fractions : rendre
irréductible
|
|
84 |
2 |
|
90 |
2 |
|
42 |
2 |
45 |
3 |
||
|
21 |
3 |
15 |
3 |
||
|
7 |
7 |
5 |
5 |
||
|
1 |
|
1 |
|
84 = 22 3 7 ; 90 = 2 32 5
PPCM = 22 32 57 = 1260
Application
aux fractions : réduire au même dénominateur :
; 
; 
|
|
45 |
3 |
|
120 |
2 |
|
54 |
2 |
|
|
15 |
3 |
60 |
2 |
27 |
3 |
||||
|
5 |
5 |
30 |
2 |
9 |
3 |
||||
|
1 |
|
15
|
3 |
3 |
3 |
||||
|
|
|
5 |
5 |
1 |
|
||||
|
|
|
1 |
|
|
|
45 =
32 5 ; 120 = 23
3 5 ; 54 =
2 33
PPCM = 23 335 = 1080
Donc :
= 
; 
=
; 
= 
5.5 Addition et soustraction de fractions :
Pour additionner
( ou soustraire) plusieurs fractions , on
les réduit au même dénominateur , on additionne ( ou soustrait) les
numérateurs entre eux et on conserve le
dénominateur commun.
Exemple 1 : 
= 
= 
= 
Exemple 2 : 
= 
= 
= 
= 
( sous forme décimale : -0,5 )
5.6 Multiplication des fractions
Pour multiplier
2 fractions entre elles , on multiplie les numérateurs entre eux et les dénominateurs entre eux .
Exemple :
= 
= 
Note :
avant d’effectuer une multiplication de fraction , il faut
simplifier s’il y a lieu .
= 
= 
= 
5.7
Division de
fractions :
Pour diviser 2 fractions , on
multiplie la fraction dividende par l’inverse de la fraction diviseur .
Exemple : 
= 
= 
= 
= 
Exercices
sur les fractions :
1)
Rendre irréductible :
|
a) |
|
|
|
|
b) |
|
|
|
|
a) |
540 |
2 |
|
315 |
3 |
|
270 |
2 |
105 |
3 |
||
|
135 |
3 |
35 |
5 |
||
|
45 |
3 |
7 |
7 |
||
|
15 |
3 |
1 |
|
||
|
5 |
5 |
|
|
||
|
1 |
|
|
|
||
|
540
= 22 |
315
= 32 |
||||
PGCD = 325 = 45
Donc : 
= 
|
b) |
|
|
|
|
b) |
4200 |
2 |
|
24
000 |
2 |
|
2100 |
2 |
12000 |
2 |
||
|
1050 |
2 |
6000 |
2 |
||
|
525 |
3 |
3000 |
2 |
||
|
175 |
5 |
1500 |
2 |
||
|
35 |
5 |
750 |
2 |
||
|
7 |
7 |
375 |
3 |
||
|
1 |
|
125 |
3 |
||
|
|
|
25 |
5 |
||
|
|
|
5 |
5 |
||
|
|
|
1 |
|
||
|
4200
= 23 |
24
000 = 26 |
||||
PGCD = 23
3 52 = 600
Donc :
= 
2)
Effectuer l’opération
suivante :
|
|
|
|
|
|
|
|
|
|
6- MONOMES – POLYNOMES- FACTORISTAIONS
6.1 Monômes
6.1.1 Définition : Un monôme est une
expression algébrique dans laquelle les seules opérations à effectuer sont des
multiplications et des élévations à une puissance .
Exemples :
3 x2 ; 2ab ; …..
Dans
« 3x2 »
« 3 » est appelé « coefficient numérique » et
« x2 »
« partie littérale »
6.1.2 .- Somme algébrique de monômes semblables .
Note : des monômes sont dits
« semblables » si leur partie littérale est la même .
Exemple :
4 x2 + x2 + 
= x2 ( 4
+ 1 + 
) = 
La somme algébrique de monômes semblables est un
monôme semblable dont le coefficient
numérique est la somme algébrique des coefficients numériques des monômes donnés .
6.1.3 – Produit de deux monômes
exemples : ( 3 x ) ( 2 x ) = 3 x 2 x = 32xx = 6 x2
Le produit de plusieurs monômes est un
monôme :
-
dont le coefficient
numérique est le produit des coefficients
numériques ( en observant la règle des signes
) ;
-
dont la partie littérale
comprend toutes les lettres contenues dans les monômes ,
chacune d’elles étant affectées d’un exposant égal à la somme de ses exposant
dans les facteurs .
6.1.4 –Quotient de deux monômes :
exemple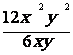 
= 
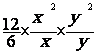= 2 xy
ou = 2 x 2-1 y 2-1 = 2xy
6.2.
Polynômes :
6.2.1
Définition
Un polygone est une somme algébrique de monômes.
Exemple :
3 x –4 ; -x2 +3
x – 4 ; x2y – 2 x y + x y2
Soit le polynôme : 3 ax2 - 1 + 6x + 5 – 3x – a x2
Devant cette somme algébrique de monômes semblables , il est nécessaire de grouper les monômes
semblables :
=3 ax2
- 1 + 6x + 5 – 3x – a x2
= 2 ax2 + 3x + 4
On a opéré la réduction des termes semblables .(voir factorisation SOScours)
Un polynôme doit toujours être réduit et ordonné .
6.2.2
ADDITION de polynômes .
La
somme de plusieurs polynômes s’obtient
en écrivant leurs termes ( avec leurs signes ) les uns
à la suite des autres .
Exemple :
A = + a2 + 2a – 1 ; B = + 3 a
² - 6 a + 7
A + B = + a2 + 2a – 1 + 3 a ² - 6 a + 7 = 4
a² +- 4 a + 6
6.2.3
- Soustraction de deux polynômes .
Généralement pour gagner du temps on applique les 2
règles pratiques suivantes .
- une parenthèse
précédé du signe « + » peut – être supprimée sans que les signes
contenus à l’intérieur de cette
parenthèse soient modifiés .
-
une parenthèse précédé du signe « + » peut – être
supprimée à condition de changer tous les signes contenus à l’intérieur de
cette parenthèse .
Exemple : A =
x² -x +1 ; B = 2x² +x –3 ;
C = 5x² - 4x +4
A + B – C = (x² -x +1 ) +( 2x² +x –3) - ( 5x² - 4x +4)
= x² -x +1 + 2x² +x –3 - 5x² + 4x - 4
A + B - C =
2x² +4x - 6
6.2.4
– Multiplication de
polynômes ( SOS
Rappels)
-
Produit d’un polynôme par
un nombre ou «monôme »
Pour multiplier un polynôme par un monôme , on multiplie
successivement chaque terme du
polynôme par le monôme .
Exemple : -3a ( 2a + b
) =
(-3 a) (2a) + -(3a) ( b) = -6a² -
3ab
-
Produit de 2 polynômes
Pour
multiplier deux polynômes , on multiple chaque terme
du premier par chaque terme du second .
Exemple :
( x
+ 1 ) ( 2x +
3) =
( x 2x ) + ( 3 fois x ) + ( 1 fois 2x) + ( 1
fois 3)
= 2x² + 3x + 2x +
3
= 2x² + 5x + 3
6.3
.- Identité remarquables
Certaines identités , très
souvent utilisées , sont qualifiés de
remarquables ; elles doivent être connues de mémoire .
Pour tout réel , a , b , c
, on a
( a + b ) ² = a ² + 2a b + b²
( a - b ) ² = a ² -
2a b + b²
( a + b ) ( a – b) = a² -
b²
( a + b )3 = a 3
+ 3 a² b + 3 ab² + b 3
( a - b )3 = a 3
- 3 a² b + 3 ab² - b 3
a3 + b 3 = ( a + b )
( a² - ab + b2 )
a3 -
b 3 = ( a - b ) (
a² + ab + b2 )
6.4
Factorisation
La factorisation est l’opération inverse du
développement :
|
a ( b + c ) |
|
|
|
|
!’développement!’ |
ab + ac |
!’factorisation!’ a ( b
+ c ) |
|
Factoriser un polynôme , c’est le décomposer , quand cela est possible , en un produit de 2 ou plusieurs facteurs .
Dans certains cas , la
factorisation peut-être effectuée à l’aide des identités
remarquables : x4 - 1 = ( x²)² - 1 ² = ( x² +1) ( x² -1)
Ici le polynôme ( x4
– 1 ) a été décomposé en produit
de 2 facteurs
Mais bien souvent les identités remarquables ne
sont pas utilisables , il faut alors trouver un
facteur commun à tous les termes du
polynôme.
16 a + 16 b + 16 c = 16 ( a + b + c )
4 a² + 5 a3+ a6 = a²
( 4 + 5 a + a4 )
ici le
« a² » est commun à tous les termes
du polynôme car on peut
écrire :
4 a² + ( 5a
« fois » a² ) + ( a4
« fois » a² )
Exercices sur les monômes ; polynômes – factorisation
Monômes :
Calculer
|
a |
|
|
|
|
b |
|
|
|
Polynômes :
|
a |
( 3x²
- 2x –1) – (-x² +x –4) |
|
|
|
b |
( x
– 2) –( x+ 3 ) + ( x-4) – ( 2x –5) |
|
|
|
C |
( x²
+ x – 1) – ( -2x² + +x +3 ) – ( x² - x +1) |
|
|
|
D |
(5-x) ( 3x – 5 ) |
|
|
|
E |
( 7
+ x ) ( -3 – x ) |
|
|
|
f |
b (x + a –b) – a ( x + b
–a) – ( a² - b²) |
|
|
Factoriser les expressions suivantes :
|
A |
|
|
|
|
B |
a3 + a² |
|
|
|
C |
5x4 + 10 x² |
|
|
|
D |
X² + 2xy+y² |
|
|
|
E |
x² - |
|
|
|
f |
m² x² - n² y² |
|
|
7_ FRACTIONS RATIONNELLES
( on dit aussi : expression algébrique
rationnelle fractionnaire )
7
.1 – Définition
Une fraction rationnelle est une fraction dont les
2 termes sont des monômes ou des polynômes .
Exemple : 
; 
; 
7.2
Propriété fondamentale
Lorsqu’on multiplie
ou divise les 2 termes d’une fraction
rationnelle par une
expression algébrique non nulle , on obtient
une fraction rationnelle égale.
Exemples : 
= 
= 
= 
7.3. Simplification des fractions rationnelles.
Pour simplifier une fraction rationnelle
, il faut diviser ses deux termes par un facteur commun non nul .
a)
les deux termes sont des
monômes
= 
= 
les
deux termes sont divisés par le facteur
« x » ; avec « x différent de 0»
b)
l’un des termes est un polynôme , l’autre un monôme .
= 
= 
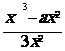les
deux termes ont été divisés par le facteur « x² » ( x ¹ 0
)
c)
les deux termes sont
polynômes
= 
= 
les 2 termes
ont été divisés par le facteur ( x+1) ; avec x ¹ -1
8
.4 Réduction au même dénominateur
Même
procédure que pour les fractions ordinaires :
-
Simplification des
fractions.
-
Choix d’un dénominateur
commun qui sera un produit de facteur divisible par chacun des dénominateurs .
-
Réduction de chaque
fraction au dénominateur commun en multipliant les 2 termes par un même facteur
convenable .
Exemples : 
; 
; 
dénominateur commun
« 4x² »
= 
; 
= 
;
7.5
Addition et soustraction
des fractions rationnelles .
Même règle que pour les fractions ordinaires :
-
Réduction au même dénominateur .
-
Addition ou soustraction
des numérateurs .
-
Maintien du dénominateur commun .
Exemples : 
+
+ 
= ? Dénominateur Commun ( x . 5 . y)
+ 
+ 
= 
+ 
+ 
= 
7.6
– Multiplication et
division des fractions rationnelles
Mêmes règles
que pour les fractions ordinaires :
-
pour multiplier des
fractions rationnelles
, on multiplie les numérateurs entre eux et les dénominateurs
entre eux .
-
Pour diviser 2
fractions rationnelles
, on multiplie les
numérateurs entre eux et les
dénominateurs entre eux .
-
Pour diviser 2 fractions rationnelles ,
on multiplie la première par l’inverse de la seconde ;
Note : Toujours simplifier les fractions avant d’
effectuer les produits.
Exemples 
= ?
Simplification ( x² -1 ) =
( x+ 1)( x-1 )
Þ 
= 
Simplification par ( x+1)
avec « x » ¹ (
-1)
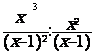= ? Û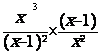 
= 
= 
= 
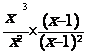simplification
par x² ( x ¹ 0 ) et ( x-1) ( x¹ 1)
Exercices sur les fractions rationnelles ;
1°) simplification : simplifier les fractions rationnelles
ci –dessous
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2) Additions et soustractions .
Effectuer les opérations suivantes et simplifier.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3)
Multiplications et
divisions
Effectuer les opérations suivantes et simplifier .
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8- EQUATION DU 1er DEGRE A
UNE INCONNUE
les
équations du 1er degré à une inconnue sont de la forme :
2x +
7 = 5 x + 3 ( « x »
est l’inconnue)
Pour résoudre une équation du 1er degré à une inconnue ,
on doit « isoler » l’inconnue
dans un des 2 membres . Pour cela ,
on a 2 règles :
a)
On peut ajouter
ou retrancher une même expression aux
deux membres d’une équation .
Exemple : pour avoir tous les
« x » dans le premier membre
et tous les nombres , on
va additionner aux 2 membres de l’équation ci dessus :
( 2x + 7 = 5 x +
3 )
les termes ( -5x ) et ( -7)
ainsi
: 2x + 7 = 5 x + 3
( -5x ) + 2x + 7 = 5 x
+ 3 + ( -5x ) ( l'égalité reste vraie)
-3 x +
7 + (-7 ) = + 3 + ( -7) (après
simplification , l'égalité reste vraie)
-3x = -4 (après simplification , l'égalité reste vraie)
b)
On peut
multiplier les 2 membres d’une équation par un même nombre différent de zéro .
Exemple : 
x - 3x
= - 4 x
Û x =
Exemple
de résolution d’équation :
+ 2 
= 3 x +
On met tout sous le même dénominateur (4) :
+ = 
+
On chasse le dénominateur : 30x +
8 -21x = 12x +1
30x – 21 x
– 12x = 1 – 8 Û - 3x = -7
on divise les 2
membres par (-3) ; ou on multiplie par
- 3x = -7
x
= 
S = 
Equations qui se ramènent au premier degré :
( x –
3 ) ( x + 4 ) = 0
Pour que le premier membre soit nul
, il faut et il suffit que l’un des facteurs soit qui le compose soit
nul .
x-3 = 0 Û x = 3
x+4 = 0 Û x = -4
Þ 2
racines : S = 
Equations
où l’inconnue figure au
dénominateur :
+ 
= 3,5
cette
équation n’a de sens que si ( x – 1) est ¹ 0 Þ x ¹ 1
+
= 
On multiplie les 2 membres de l’équation par 2(x-1)
8 + 3x
–3 = 7x –7
3x-7x = - 7 + 3 – 8
-4x =
-12
x = 
= 3 S = 
Cas particuliers :
3x – 7 = 5x –4 –2x + 11
Û 3x – 5x + 2x = 7 – 4 + 11
Û
0x = 14
0 = 14
ß
impossible
S = 
exemple :
3x –
7 = 5x –4 –x + 11 –3 –x –5 –6
Û
3 x – 5x + x +x = 7 –4
+11-3 –5 –6
Û
0x = 0
Û
=0 =0
vraie
Quel que soit « x » Þ S =
R ( réels)
Exercices :
Résoudre :
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= 
= 
8
.- INEQUATION 1er DEGRE 1 INCONNUE
Une inéquation est composée de 2 termes et d’un
signe d’inégalité :
³
supérieur ou égal
£
inférieur ou égal
> supérieur strictement
< inférieur strictement
exemples :
exemples : 7x + 5 ³
6 ;
+ 7 < 8 x +
4 ; ……..
Comme pour une équation ,
il faut isoler « x » d’un côté
du signe . Pour cela , on peut additionner aux
2 membres un même nombre ou multiplier les 2 membres ( tous les termes) par un
même nombre .
Note : si on multiplie
les 2 membres ( tous les termes) par un nombre
négatif , il faut inverser le signe
d’inégalité
.
Exemple : 9x + 7 < 15 x + 4 Û 9 x -
15 x < 4 –7
Û
-6x < -3
Note : pour enlever ( -
6) devant x , on multiplie les deux membres ( ici 2 termes) par (
) et on a inversé le digne de l’inégalité
x >
+ 
Û x >
Interprétation du résultat :
x³
8 L’ensemble de solution contient tous
les « x » supérieur ou égal à « 8 » . Notation : [ 8
; +¥ [
x£ 8
L’ensemble de solution contient tous les « x » inférieur ou
égal à « 8 » . Notation : ]
- ¥ ; +
8 ]
x> 8 L’ensemble de
solution contient tous les « x » supérieur à « 8 » .
Notation : ] 8
; +¥ [
x<8
L’ensemble de solution contient tous les « x » inférieur à
« 8 » . Notation : ]
- ¥ ; +
8 [
Exercice : résoudre :
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10. - SYSTEME D’EQUATIONS DU 1er DEGRE A 2 INCONNUES.
Les systèmes d’équations du 1er degré à
2 inconnues sont de la forme :
2x +5y =1
4x-3y = 15
Il admettent en général une solution
, il existe plusieurs méthodes de résolution , nous en retiendrons
2 :
en retiendrons 2 :
-Résolution par addition.
-Résolution par substitution.
10.1 Résolution par addition :
règle :
a) Multiplier les 2 membres de chaque
équation par des nombres choisis de telle façon que les coefficients de l’une
des inconnues deviennent symétriques .
b)-Additionner les 2 équations membre à membre .
c)
Résoudre l’équation obtenue .
d)
Calculer la valeur
numérique de l’autre inconnue
.
Exemple : Reprenons le système cité plus
haut :
2x +5y =1
4x-3y = 15
a)
rendre symétrique les
coefficients de l’une des inconnues :
( -2) ( 2x +5y) =( -2) 1
4x-3y = 15
ß
-4 x +-10 y =-2
4x -3y
= 15
b)
Additionner les 2 équations
membre à membre :
-4 x +-10 y + (4x -3y) =
-2 + 15
Û - 13 y = 13
c)
résoudre l’équation
obtenue :
- 13 y = 13 Û y = -
Û y = -
1
d)
Calculer la valeur
numérique de l’autre inconnue ; on remplace ,
dans l’une des équations , y par sa valeur : 2x + 5
( -1) = 1
Û
2x = 1 + 5
Û
x = 
= 3
10.2 – Résolution par substitution
règle :
a)
Calculer l’expression de
l’une des inconnues en fonction de
l’autre dans l’équation la plus simple .
b)
Substituer à l’inconnue choisie ,
DANS L’AUTRE EQUAION , l’expression ainsi
calculée .
c)
Résoudre l’équation
obtenue.
d)
Calculer la valeur de
l’autre inconnue en utilisant
l’expression calculée .
Exemple :
Résoudre le système :
7x-
5y = 16
x +
11y = 14
a)
Calculons « x »
dans la 2ème équation :
x + + 11 y
= 14 Û x =
14 – 11y
b)
Substituons cette expression à « x » dans la 1ere équation :
7 ( 14 -
11 y ) -
5 y = 16 Û 98 – 77y –5y = 16
c) Résolvons l’équation :
98 – 77y –5y = 16 Û - 82 y
= - 82
Û
y = 1
c)
Utilisons cette expression
pour calculer « x »
X = 14 – 11 Û x = 3
Exercices :
|
|
2x +3 =
6y 5y –2 =
3x |
|
|
|||
|
|
|
|
|
|||
|
|
4x – 7y =
- 3 7x + 4y =
36 |
|
|
|||
|
|
5x –2y
= 77 |
|
|
|||
|
|
x 5x |
|
|
|||
|
|
2,25 x
+ 1,5 y = 30 7,5
x – 2 y = 65 |
|
|
= 1
Exercices sur les systèmes d’équations :
Résoudre par la méthode d’addition ou substitution
les systèmes ci – dessus.
|
|
Résoudre par la méthode d’addition : 2x + 3 =
6y 5y –2 =
3x |
|
|
|
|
Résoudre par la méthode de substitution : 4x – 7y
= -3 7x +4y
= 36 |
|
|
|
|
Résoudre par la méthode d’addition ou
substitution |
|
|
11.6 EQUATION DU
2ème DEGRE A UNE INCONNUE
On appelle « équation du second degré à une
inconnue » ; toute équation de la forme : ax² + b x +
c = 0
Une équation du 2ème degré est incomplète quand l’un des
coefficients « b » ou « c » est nul .
Si le coefficient de « a » = 0 , elle se ramène à une équation du 1er
degré .
1)
Calcul du
discriminant : D = b² - 4ac
1er cas : Si D
> 0 ,
l’équation a deux racines distinctes .
2ème cas : Si D =
0 ; l’équation a une racine double.
3ème cas . Si D
< 0 ,
l’équation est impossible . ( voir les complexes)
2)
Calculs des racines :
Si D > 0 : 1ère racine
x’ = 
2ème
racine : x’’ = 
si D = 0
Racine double : x’ =
x’’ =
si D < 0
pas de résolution de l’équation
Exercices sur les équations du 2ème degré à une inconnue.
|
|
x² - 16 x
+ 65 = 0 |
|
|
|
|
x² - 13 x
– 48 = 0 |
|
|
|
|
( x
– 9 ) ² - 49 = 0 |
|
|
|
|
x² - 16 x + 63 = 0 |
|
|
|
|
x² - 10 x + 25 = 0 |
|
|
|
|
( x
+ 5 ) ² - 4x – 20 = 0 |
|
|
|
|
|
|
|
|
|
( 3x
–7)² - 4 (x + 1 ) ² = 0 |
|
|
= 0
CORRECTION Exercices :
Monômes –
Polynômes – Factorisation
Calculer
|
a |
|
|
|
|
b |
|
|
|
= 
=
Polynômes :
|
a |
( 3x²
- 2x –1) – (-x² +x –4) |
= 3x²-2x-1+x²-x+’ =4x² - 3x + 3 |
|
|
b |
( x
– 2) –( x+ 3 ) + ( x-4) – ( 2x –5) |
=x-2-3+x-4-2x+5 =-x-4 |
|
|
C |
( x²
+ x – 1) – ( -2x² + +x +3 ) – ( x² - x +1) |
=x²+x-1+2x²-x-3-x²+x-1 = 2x²+x-5 |
|
|
D |
(5-x) ( 3x – 5 ) = 5 |
=15x-25-3x²+5x = -3x² +20x - 25 |
|
|
E |
( 7
+ x ) ( -3 – x ) 7 |
=-21 –7x –3x – x² = -x² -10x -21 |
|
|
f |
b (x + a –b) – a ( x + b
–a) – ( a² - b²) = bx +ba + -b |
= b x -a x = x ( b –a) |
|
Factoriser les expressions suivantes :
|
A |
30a + 60 b |
|
|
|
B |
a3 + a² |
a² ( a+ 1) |
|
|
C |
5x4 + 10 x² |
5x² ( x² +2) |
|
|
D |
x² + 2xy+y² |
( x + y ) ² |
|
|
E |
x² - |
= x² - |
|
|
f |
m² x² - n² y² |
(m x)² - (n y)² = ( m x
+ n y) ( m x – n y) |
|
= 
