Pré requis:

LES EGALITES
Calcul numérique : nomenclature.
« algèbre » : les conventions d’écriture.
Lecture : Inégalité ou inéquation
Les relations d’ordre(symboles )
Les intervalles

ENVIRONNEMENT du dossier:

DOSSIER Calcul Numérique:

LES « INEGALITES » N°1 : Définition ; propriétés ; les théorèmes

	Cours n°1 : Les inégalités ; la double inégalité.
	Cours n°2 : Les inégalités algébriques .
	· Définition.
	· Propriétés.
	· Théorèmes sur les inégalités .




			Travaux auto formatifs.
TEST		COURS	Devoir Contrôle	Devoir évaluation	Interdisciplinarité	Corrigé Contrôle	Corrigé évaluation

COURS N°1

Les INEGALITES.				Info ++ voir Fiche 4 +
Nous avons déjà rencontré des « inégalités » à l’école élémentaire ; par exemple : 3 < 7 ( qu’il faut lire : 3 est inférieur à 7) ; on dit aussi : « 3 est plus petit que 7 » ou 9 > 4 ( qu’il faut lire : 9 est supérieur à 4 ) ; on dit aussi : « 9 est plus petit que 4 » En voici d’autres :
on lit : le nombre « x » est inférieur ou égal à 9			on lit : le nombre « y » est supérieur ou égal à 3
Ce sont des phrases mathématiques , dont le verbe est représenté par un des quatre signes : : < ; > ; ou
On retiendra :
« a » et « b » représentent des nombres
	La phrase mathématique :	Se lit en écriture littérale
	« a > b »	« a » est strictement supérieur à « b »
	« a < b »	« a » est strictement inférieur à « b »
	« a b »	« a » est supérieur ou égal à « b » et signifie : « a > b » ou « a = b »
	« a b »	« a » est inférieur ou égal à « b » et signifie : « a < b » ou « a = b »

Remarque 1 : « x » et « y » représente des nombres ; « x > y » a la même signification que « y < x »
Remarque 2 : Comme pour les égalités, dans toute égalité, on parle de : « membre de gauche » et « membre de droite ; ou de « premier membre » et « deuxième membre ».

Exercice : Compléter en utilisant convenablement > ou < .

14 ……………7 ; 27 ……………………34 ; 126 …………18 ; 248 ………………. 5462

Vocabulaire :
- 9 > 5 et 13 > 7 sont des inégalités de même sens . - Il en est de même pour 5 < 7 et 8 < 11 ou ou x y et m 6 - 9 > 5 et 5 < 7 sont des inégalités de sens contraire.
Exercices : Ecrire des inégalités de même sens : ………………………………………………………………………………. Ecrire des inégalités de sens contraire : ……………………………………………………………………………

DOUBLE INEGALITE.				Info plus.
Considérons les deux inégalités de même sens : 7 < 13 et 13 < 39
Dans la suite naturelle des nombres entiers naturels, « 7 » est placé avant « 13 » , et « 13 » est placé avant « 39 »., on a donc « 7 » est placé avant « 39 » On condense ces 3 inégalités par une double inégalité : 7 < 13 < 39 ; les nombres « 7 ; 13 ; 39 » sont alors rangés dans l’ordre croissant. · On peut faire de même avec plusieurs inégalités de même sens : 7 < 13 ; 13 < 39 ; 39 < 67 , on écrit alors : 7 < 13 < 39 < 67 · On peut faire de même avec les : > ; ou
Attention : Dans le cas 4 < 13 et 13 > 11 , on ne peut pas écrire 4 < 13 > 11 par ce que les nombres ne sont ni rangés par ordre croissant ni dans l’ordre décroissant.
Exercice : on vous donne des phrases mathématiques , barrer celles qui sont fausses ou incorrectes :
33 > 15 < 17	15 17 > 8	27 < 54 > 16	27 27 59
115795	43 79 43	16 < 13 < 19	23 < 47 < 47

Exercice 1 :
En utilisant le signe < ; ranger dans l’ordre croissant les nombres suivants : 13 ; 43 ; 8 ; 132 ; 27 ;55 ;2 ; 139 …………………………………………………………………………………………………………………………………………………………………………………….
Exercice 2 : Ranger dans l’ordre décroissant les nombres suivants en utilisant le symbole convenable.: 15 ; 43 ; 9 ; 133 ; 27 ;65 ; 2 ; 169 ……………………………………………………………………………………………………………………………………………………………………………………….

COURS N°2

RAPPELS : Un nombre algébrique « a » est plus grand qu’un nombre algébrique « b » , lorsque la différence ( a – b ) est positive.

Se rappeler :

Exemple :

soit deux nombres : « a » = + 4 et « b » = -5

La différence de ces deux nombres est : (+4) – (-5) = +9 SOS cours

On écrira que le nombre ( + 4 ) est plus grand que ( - 5)

Se rappeler :

Comparaison de deux nombres relatifs	Pré Requis :SOS Cours
Un nombre négatif est inférieur à un nombre positif !

1°) Définition :

· On sait qu’une quantité « a » est dite « plus grande » ou « plus petite » qu’une quantité « b » , selon que la différence algébrique « a – b » est « positive » ou « négative » .

· Toute quantité positive est dite « plus grande que zéro » et toute quantité négative est dite « plus petite que zéro » ;

· L’inégalité « a > b » peut donc s’écrire sous chacune des formes équivalentes suivantes : « a – b > 0 » ; « a= b + k² » ; « a – b = k² » ; « b < a » ; « b – a < 0 » ; « b = a – k² ».

On dit qu’un nombre « a »est supérieur à un nombre « b » si pour obtenir « a » il faut ajouter à « b » un nombre « positif » ou , ce qui revient au même, si la différence « a - b » est un nombre positif.

On appelle aussi « inégalité » une formule par laquelle on exprime que de deux quantités ,l’une est supérieure à l’autre , ainsi , si l’on veut exprimer que « 4 » est « supérieur » à « 3 » , ou « 4 » est « plus grand » que « 3 » , on écrit : 4 > 3

Que l’on énonce « 4 » supérieur à « 3 » .

On peut écrire aussi : 3 < 4 que l ‘on énonce « 3 inférieur à 4 ».

Ces deux inégalités sont dites de « sens différents ».

On voit que l’on peut permuter les deux membres d’une égalité à condition d’en changer le sens.

Grâces aux remarques présentées plus haut , nous pouvons écrire les égalités suivantes :

Les inégalités suivantes sont vraies	Parce que : Le plus grand moins le plus petit le résultat est positif
- 4 < -3
-2 > -7
-2 < 0
-5 < 1

Calcul numérique : nomenclature.

2°) Propriétés :

1°) Tout nombre positif est plus grand que zéro.

2°) Tout nombre négatif est plus petit que zéro.

3°) Tout nombre positif est plus grand que tout nombre négatif.

4°) De deux nombres positifs le plus grand est celui qui a la plus grande valeur absolue.

5°) De deux nombres négatifs le plus grand est celui qui a la plus petite valeur absolue.

3 °) Théorèmes sur les inégalités :

Théorème I :

On peut ajouter ou retrancher une même expression aux deux membres d’une inéquation.

On ne modifie pas le sens d’une inégalité en ajoutant ou retranchant un même nombre à ses deux membres.

Exemple 1 :, l’on a : -4 < -3

L’on a aussi

	- 4 + 12< -3 + 12
	- 4 –15 < -3 – 15

C’est à dire :

	8 < 9
	- 19 < -18

D’une manière générale, si l’on a :

Hypothèse .

a > b

Conclusions :

Conclusion 1	a + c > b + c
Conclusion 1	a - c > b - c

« c » désignant un nombre quelconque.

En effet ,par définition , l’inégalité : a > b , signifie que la différence « a » - « b » est positive , ce que l’on écrit a -b > 0

Or le calcul algébrique nous a appris que l’on a :

a + c-(b + c) = a- b

Donc si ( a- b ) est positif , il en est de même de a + c – ( b + c ) c’est à dire que l’on a : a +c – ( b + c ) > 0

Ce qui revient à écrire :

a + c > b + c

La démonstration se ferait d’une façon analogue pour le cas de la soustraction.

Soit l’équation 5 x + 12 > 4 - 3x (1)

Nous en déduisons, en ajoutant 3x + 12 aux deux membres :

5x +12 +3x - 12 > 4 - 3x + 3 x - 12

soit 5 x + 3x > 4 - 12

1° Application. - Dans l’exemple précédent , les termes - 3x et + 12 de l’inéquation (1) sont devenus +3x et - 12 dans l’inéquation (2) ; de plus ils ont changé de membre. Donc :

Dans une inéquation, on peut faire passer un terme d’un membre à l’autre , à condition de changer le signe qui le précède.

2°) Degré d’une inéquation entière :

Si les deux membres d’une inéquation sont des polynômes, on dit que l’inéquation est entière.

En faisant passer tous les termes dans le premier membre, l’autre se réduit à zéro. Le degré, par rapport à l’ensemble des ses lettres inconnues, du polynômes ainsi obtenu dans le 1^er membre est le degré de l’inéquation.

Ainsi : 5 x - 3 > 0 est du premier degré.

3 x² - 5x - 1 < 0 est du second degré.

x ³ - x > 0 est du troisième degré.

Théorème II :

1°) Etant donnée une inégalité, on obtient une inégalité de même sens en multipliant ses deux membres par un même nombre « POSITIF »

- On peut multiplier ou diviser les deux membres d’une inéquation par un même nombre positif en conservant le sens de cette inéquation.

Ainsi : On ne modifie pas le sens d’une inégalité en multipliant ou divisant les deux membres par un même nombre positif.

2°) Si on multiplie par un nombre « NEGATIF » on doit CHANGER LE SENS de l’inégalité.

- On peut multiplier ou diviser les deux membres d’une inéquation par un même nombre négatif , à condition de changer le sens de cette équation.

Ainsi : On modifie ce sens en multipliant ou divisant les deux membres par un même nombre négatif.

EXEMPLES :

Par exemple : On a 2 < 4

En multipliant les deux membres par « 3 » , on obtient : 6 < 12

Et en les divisant par 8 , on obtient :

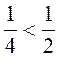
On obtient des inégalités de même sens que l’inégalité proposée .

Au contraire , en multipliant les deux membres de l’inégalité primitive 2 < 4 ; par –2 , on obtient le résultat : - 4 < - 8

et en divisant 2 < 4 par – 2 on obtient : -1 < -2

Pour démontrer ce théorème 2 , il suffit d’observer que le produit d’un nombre par un nombre positif est du même signe que le multiplicande , tandis que le produit d’un nombre négatif , est de signe contraire à celui du multiplicande , si donc on a :

	a < b
C’est à dire	a - b > 0
Si « c » est positif , on a aussi	( a – b ) c > 0
C’est à dire	ac- b c > 0
Ou bien	ac> b c
Si « c » est négatif , on a
	( a – b) c < 0
	ac - b c < 0
	ac< b c
La démonstration est la même dans le cas de la division .

Résumé du théorème II :

Hypothèse : .

a > b

Conclusions :

am > bm

a m < b m

Si m > 0

Si m < 0

Autre application :On veut « réduire cette inéquation » en vu d’une « résolution »

1°) De L’inéquation :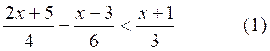

On en déduit, en multipliant les deux membres par « 12 » , l’inéquation suivante :

3 ( 2x+5) - 2 (x-3) < 4 ( x+ 1) (2)

remarque : (1) et (2) sont de même sens ( même signe < )

2°) De l’équation 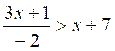(1)

on déduit, en multipliant les deux membres par -2 , l’inéquation suivante :

3x +1 < - 2 ( x + 7) (2)

remarque : (1) et (2) sont de sens contraires ( > et < ) :

Applications

1°) on peut supprimer les dénominateurs d’une inéquation en multipliant ses termes par un multiple commun positif des dénominateurs.

C’est en effet ce que montre le premier exemple précédent.

2°) On peut simplifier une inéquation en divisant ses termes par un même nombre positif.

Soit 5x - 35 > 20

En divisant les deux membres par +5 , nous obtenons : x - 7 > 4

3°) On peut changer les signes des deux membres d’une inéquation à condition d’en changer le sens .

cela revient à multiplier les deux membres de l’inéquation par « -1 »

ainsi : - 3 x < 21 Û à 3 x > -21

de même : on peut changer les deux membres d’une inéquation à condition d’ en changer le sens.

Théorème 3

En élevant les deux membres d’une inégalité au carré on obtient une inégalité « DE MEME SENS si les deux membres sont « positifs » et une inégalité DE SENS CONTRAIRE s’ils sont « négatifs ».

On ne modifie pas le sens d’une inégalité en élevant au carré les deux membres dans le cas où ils sont positif tous les deux :

Par exemple :

3 < 8

En élevant les deux membres au carré on obtient :

3 ² = 9 ; 8 ² = 64

9 < 64

Remarque :1

Si les deux membres sont négatifs , l’élévation au carré change le sens de l’inégalité

Soit	-5 < -3
On obtient en élevant au carré : 25 < 9 ce qui n’est pas vraie donc on change le sens de la relation d’ordre : 25 > 9

Remarque 2

Dans le cas où les deux membres sont de signes différents , aucune règle ne peut prévoir si le sens devra être maintenu.

Ainsi

	-2 < 3
Donnera	4 < 9

Tandis que l’inégalité :

	-5 < 2
Donnera	25 > 4

Dans le premier exemple, le sens de l’inégalité est resté le même, dans le second cas , le sens a changé.

Hypothèse

a > b

Conclusions :

a² > b² si « a » et « b » positifs.

a² < b² si « a » et « b » négatifs

Théorème 4

Etant données plusieurs inégalités de même sens on obtient une inégalité de même sens que chacune d’elles en les ajoutant membre à membre.

Hypothèse	a > b ; a’ > b’ ; a’’> b’’ ; …….
Conclusions :	a+a’+a’’+ ….. > b + b’ + b’’+…..

APPLICATIONS .

Pré requis de difficultés abordées en calcul numérique:

1°) Classement des nombres relatifs

2°) Notions sur les opérations

3°) Encadrement dans N

4°) Encadrement dans D

5°) Encadrement dans D relatif

6°) Encadrement des fractions

7° ) Les irrationnels

Les théorèmes précédents sont utilisés notamment pour comparer deux nombres , c’est à dire pour voir quel est le plus grand, lorsque cette comparaison n’est pas immédiate.

En particulier, on les emploiera pour comparer deux expressions numériques « irrationnelles ». Ils permettront de faire cette comparaison sans qu’il soit nécessaire (@ )d’extraire de racine carrée.

Ainsi soit à comparer les deux nombres :

3 + et 4 +

est compris entre 3 et 4 et entre 2 et 3 .

Les deux nombres donnés sont donc tous deux compris entre 6 et 7 et on ne voit pas immédiatement quel est le plus grand.

Pour cela regardons si on a : 3 + < 4 +

Pour cela il suffit de voir si on a : < 1 + ( Application sur théorème 1)

C’est à dire , puisque les deux membres sont positifs, si :

() ² < ( 1 + )²	( Application sur théorème 3)
13 < 8 + 2	( Application développement de (a+b)²
5 < 2	( Application sur théorème 1)
25 < 28	( Application sur théorème 3)

Cette inégalité est bien vraie. Donc 3 + < 4 +

TRAVAUX AUTO FORMATIFS.

CONTROLE :

1°) Quand dit – on qu’un nombre algébrique « a » est plus grand qu’un nombre algébrique « b » ?

2°) Citer les 4 théorèmes relatifs aux inégalités.

EVALUATION

Les inégalités suivantes sont – elles vraies ?	1°) Prouvez par un calcul : et ensuite 2°) le montrer à partir d’une droite graduée.
- 4 < -3
-2 > -7
-2 < 0
-5 < 1

Comparer les deux nombres :

3 + et 4 +

CONTROLE :corrigé

1°) Quand dit – on qu’un nombre algébrique « a » est plus grand qu’un nombre algébrique « b » ?

Un nombre algébrique « a » est plus grand qu’un nombre algébrique « b » , lorsque la différence ( a – b ) ) est positive

2°) Citer les 3 théorèmes relatifs aux inégalités /

Théorème 1

On ne modifie pas le sens d’une inégalité en ajoutant ou retranchant un même nombre à ses deux membres.

Théorème 2 .

A ) On ne modifie pas le sens d’une inégalité en multipliant ou divisant les deux membres par un même nombre positif.

B ) On modifie ce sens en multipliant ou divisant les deux membres par un même nombre négatif.

Théorème 3

On ne modifie pas le sens d’une inégalité en élevant au carré les deux membres dans le cas où ils sont positif tous les deux .

Remarque :1

Si les deux membres sont négatifs , l’élévation au carré change le sens de l’inégalité

Remarque 2

Dans le cas où les deux membres sont de signes différents , aucune règle ne peut prévoir si le sens devra être maintenu

INTERDISCIPLINARITE

RAPPELS : Un nombre algébrique « a » est plus grand qu’un nombre algébrique « b » , lorsque la différence ( a – b ) est positive.

Comparaison de deux nombres relatifs

Théorème I :

Par exemple : On a 2 < 4

Au contraire , en multipliant les deux membres de l’inégalité primitive 2 < 4 ; par –2 , on obtient le résultat : - 4 < - 8

et en divisant 2 < 4 par – 2 on obtient : -1 < -2

C’est à dire

Si « c » est positif , on a aussi

Si « c » est négatif , on a

Théorème 3

Remarque :1

Remarque 2

Théorème 4

Théorème 1

Théorème 3

Remarque :1

Remarque 2