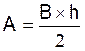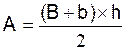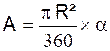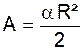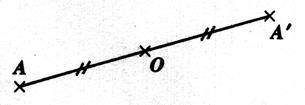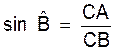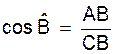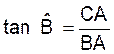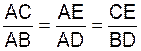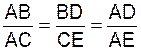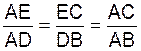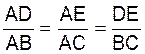LOGICIEL Pour Aide et Formation Individualisée

PAGE D ‘ENTREE

ICI pour aller directement aux informations « cours »

INFORMATIONS PEDAGOGIQUES :

DOSSIER N° 12

Matière : MATHEMATIQUE.

« TRAVAUX »

TITRE : Leçon (niveau 4) LA GEOMETRIE DANS LE PLAN ET DANS L’ESPACE.

Classe : BAC PROF. NIVEAU : IV

OBJECTIFS : - Savoir

I ) Pré requis: (pour remédiation ou mise à niveau)

i9

Géométrie plane : voir chapitre par chapitre.

:i

i9

Géométrie dans l’espace. (voir chapitre par chapitre)

:i

II ) ENVIRONNEMENT du dossier :

Index

Dossier précédent :

Dossier suivant : 1°) le parallèlisme. 2°) l’orthogonalité.

Info : Liste des cours de géométrie dans l’espace.

III ) INFORMATIONS «  formation leçon » :

Test

COURS

Travaux auto - formation.

Corrigé des travaux auto - formation.

Contrôle

évaluation

INTERDISCIPLINARITE

Corrigé Contrôle

Corrigé évaluation

Chapitres :

i9

CHAPITRE 1 : GEOMETRIE DANS LE PLAN :

:i

i9

1°) Aires des figures usuelles.

:i

i9

2°) Les Transformations

:i

i9

3°) Les Relations métriques du triangle rectangle.

i9

i9

4°) Propriété de THALES

i9

i9

CHAPITRE 2 : GEOMETRIE DANS L’ ESPACE.

i9

i9

I ) Définition du plan dans l’espace.

i9

i9

II ) Positions relatives de droites et de plans.

i9

III ) Les transformations

i9

IV) les propriétés.

i9

i9

V) Les figures géométriques usuelles et volumes.

i9

IV ) DEVOIRS ( écrits):

Devoir diagnostique L tests.



Devoir Auto - formatif (intégré au cours)



Devoir Formatif « Contrôle : savoir » ; (remédiation)



Devoir Formatif «  Evaluation  savoir faire » (remédiation)



Devoir sommatif.



Devoir certificatif : (remédiation)



* remédiation : ces documents peuvent être réutilisés ( tout ou partie) pour conclure une formation .

Leçon	Titre
	LA GEOMETRIE DANS LE PLAN ET DANS L’ESPACE.

	COURS
	CHAPITRE 1 : GEOMETRIE DANS LE PLAN :
								:i
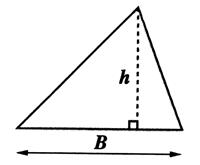
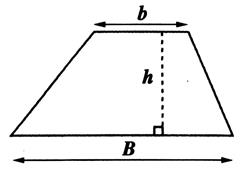
i9	1°) Aires des figures usuelles.							:i
	Aire du triangle :				Aire du trapèze :
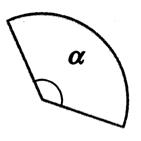
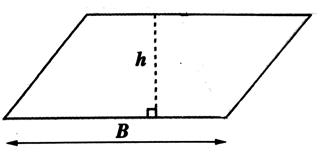
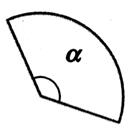
	Aire du disque :				Aire du secteur. ( a en degré)
	Aire d’un parallélogramme.				Aire du secteur : (a en radian)
i9	2°) Les Transformations							:i
	a) projection d’un point sur une droite.
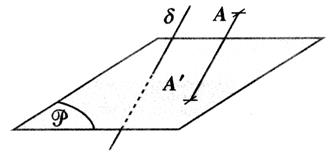
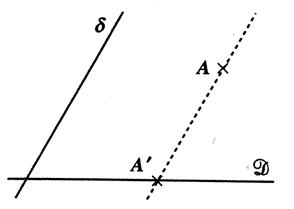
	Cas général : A’ est l’image de A par la projection suivant la droite « δ ». On dit aussi : A’ est le projeté du point A sur la droite « D » selon la direction « δ ». La droite AA’ est parallèle à la droite « delta ». on note : ( A A’) // δ .
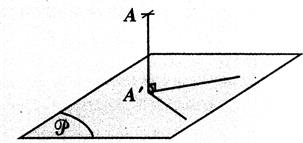
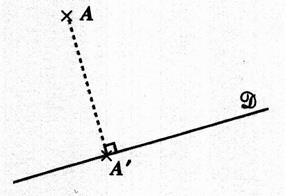
	Cas particulier : A’ est l’image de A par la projection suivant la droite « δ ». On dit aussi : A’ est le projeté orthogonale du point A sur la droite « D » selon la direction « δ ». La droite AA’ est parallèle à la droite « delta ». on note : ( A A’) // δ .  La droite AA’ est perpendiculaire à la droite « D ».
	b) Symétrie centrale.
	A’ est le symétrique de A par rapport au point « O ». Si A’ est le symétrique du point A dans la symétrie de centre « O », alors « O » est le milieu du segment noté [A A’]
	c) Symétrie axiale ( dit aussi : réflexion ou orthogonale )
i9	3°) Les Relations métriques du triangle rectangle.							i9
	►Relation de Pythagore : BC² = BA² + AC²
	►Rapports trigonométriques : on considère l’ angle B
i9	4°) Propriété de THALES							i9
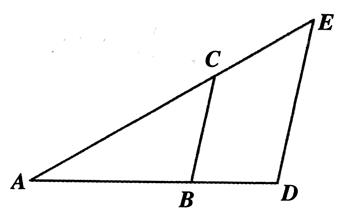
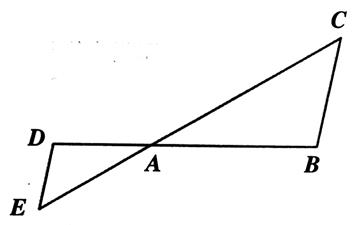
	Les droites parallèles sont du même côté.
	( ED ) et (BC) sont parallèles . Rapport de projection on peut établir la suite de rapports suivants :
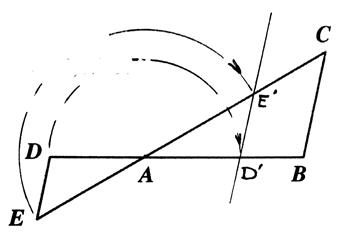
	Les droites sont parallèles, elles sont situées de part et d’autre d’un point « A ». On se retrouve dans le cas précédent si l’on fait une rotation de centre « A » au triangle (AED). « D » se retrouve en « D’ » sur la droite (AB) et « E » se retrouve en « E’ » sur la droite (AC) On peut établir la suite :
i9	Rapport d’homothétie : Les triangles ACB et AED sont dit « homothétiques », on peut donc établir la suite de rapports suivants :
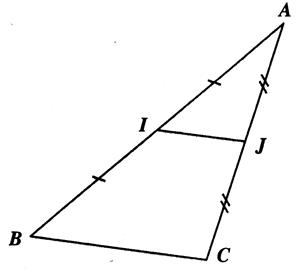
	Cas particuliers : ► Si « I » est le milieu du segment [AB] et ( IJ) est parallèle à ( BC) , alors « J » est le milieu du segment [AC]. ► Réciproquement : Si « I » est le milieu du segment [AB] et (J) le milieu du segment [AC] , alors ( I J ) est parallèle à ( BC) .							i9

i9	CHAPITRE 2 : GEOMETRIE DANS L’ ESPACE.					i9
	I ) Définition du plan dans l’espace :
i9	Représentation : le plan étant illimité , nous devons, pour pouvoir le dessiner, le limiter conventionnellement à un certain contour. Ce contour est en général un rectangle, qui , par un effet de perspective, est vu sous forme d’un parallélogramme. 2°) Observation : Dans votre chambre : les murs , le sol , le plafond matérialisent des plans : ils sont ou parallèles ou perpendiculaires , l’intersection de ces murs , plafond  ,sol forme des arêtes ; elles sont elles même ou parallèles ou perpendiculaires.					i9
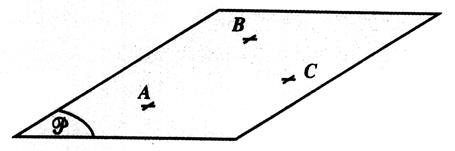
	A ) Un plan est défini par trois points non alignés :
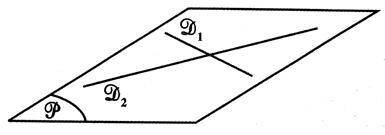
	B) Deux droites sécantes définissent un plan
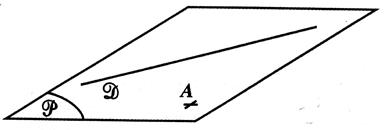
	C.) Une droite et un point n’appartenant pas à cette droite définissent un plan
	D) Un plan peut être défini par deux droites parallèles distinctes.
	II ) LES POSITIONS RELATIVES
i9	1°) Positions relatives d’une droite et d’un plan : (dans l’espace une droite peut être )					i9
	a) La droite appartient au plan elle est contenue dans le plan.
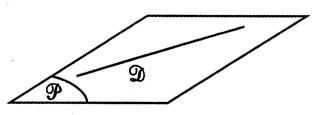
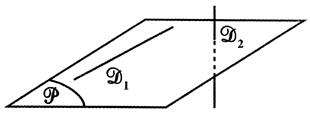
	b) La droite n’appartient pas au plan : elle est parallèle. Condition de parallélisme : pour qu’une droite soit parallèle à un plan il suffit qu’elle soit parallèle à une droite contenue dans ce plan.l
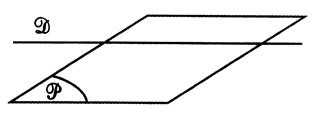
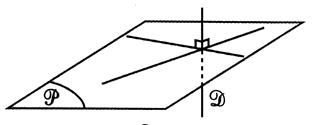
	La droite « D » est sécante au plan.
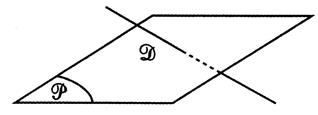
	Cas particulier : la droite « D » est sécante au plan perpendiculairement : Parce qu’elle est perpendiculaire à deux droites non parallèles du plan.
	Si une droite sécante à un plan est perpendiculaire à deux droites non parallèles de ce plan, elle est perpendiculaire au plan. (D) est perpendiculaire à (P)
	2°) Positions relatives de deux droites distinctes
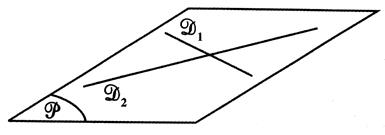
	D1 et D2 sont des droites sécantes ; ces deux droites sont « coplanaires »
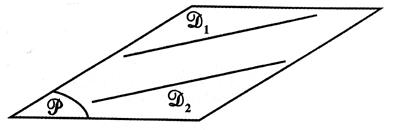
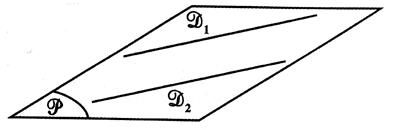
	D1 et D2 sont parallèles : ces deux droites sont coplanaires
	D1 et D2 sont non parallèles et non sécantes : ces deux droites sont non coplanaires.
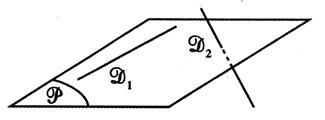
	Cas particuliers : D1 et D2 sont orthogonales et D2 est perpendiculaire au plan « P »
i9	3°) Positions relatives de deux plans distincts.
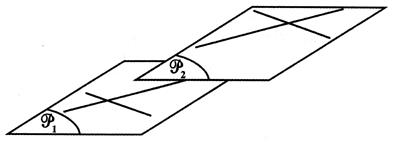
	Condition de parallélisme : Pour que deux plans ( P1) et (P2) soient parallèles il suffit que deux droites sécantes de (P1) soient parallèles à deux droites sécantes de (P2)
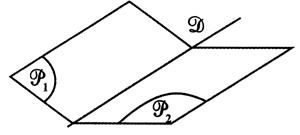
	Les plans sont sécants.
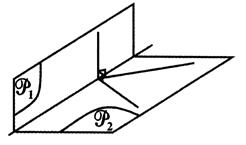
i9	Les plans (P1) et (P2) sont perpendiculaires. (P1) contient une droite orthogonale à (P2).
i9	III ) les transformations.
	Projection :Projection suivant une droite « delta »				Projection orthogonale
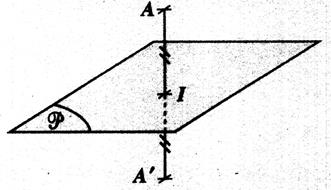
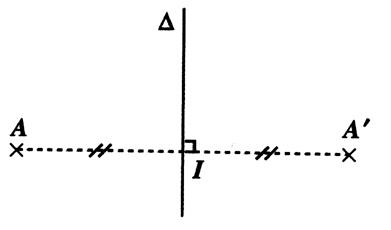
	Symétrie par rapport à un plan ( ou dit aussi : réflexion) : « A’ » est le symétrique du point « A » par rapport au plan « P ». - la droite ( AA’) est orthogonale au plan « P » - « I » est le milieu du segment [ A A’ ] - « P » est le plan de symétrie.
	IV) PROPRIETES.
	1°) Droites perpendiculaires a un plan : Pour qu’une droite soit perpendiculaire à un plan, il suffit qu’elle soit perpendiculaire à deux droites sécantes contenues dans ce plan. Si une droite est perpendiculaire à un plan, alors elle est orthogonale à toutes les droites de ce plan.
	2°) Plans perpendiculaires : deux plans sont perpendiculaires si l’un contient une droite perpendiculaire à l’autre.
	3°) Plans parallèles. Deux plans perpendiculaires à une même droite sont parallèles. Si deux plans sont parallèles, toutes droites perpendiculaires à l’un est perpendiculaire à l’autre.
	4°)Droites parallèles : Deux droites perpendiculaires à un même plan sont parallèles. Si deux droites sont parallèles tout plan perpendiculaire à l’une est perpendiculaire à l’autre.
i9 V) Les figures géométriques usuelles et volumes.						i9
i9	Info sur les volumes			Calculs :		i9
	A) Dièdre :
	Un dièdre est la figure formée par deux demi plans ayant le même bord
B) Les polyèdres.
a) Définition :
	Un polyèdre est un solide limité uniquement par des polygones plans. Un polyèdre convexe est situé d’un même côté par rapport au plan de chaque face. Un polyèdre régulier est un polyèdre dont toutes les faces sont des polygones réguliers.
b) Le prisme :
	Un prisme est un polyèdre convexe qui possède deux faces isométriques situées dans des plans parallèles. Un prisme est droit si les arêtes latérales sont orthogonales aux plans de bases.
c) La pyramide :
	Une pyramide est délimité par un polygone ( la base)) et un point n’appartenant pas au plan de la base (le sommet) ;les autres faces sont des triangles.
	C ) D’ autres solides :
a) La sphère boule
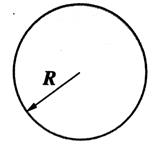
	Une sphère de centre « O » et de rayon « R » est l’ensemble des points « M » de l’espace tels que : OM = R Une boule de centre « O » et de rayon « R » est l’ensemble des points M de l’espace tels que OM £ R
b) le cylindre.
	Un cylindre droit de révolution est engendré par la rotation d’un rectangle autour de l’un de ses côtés.
d) le cône :
	Un cône droit de révolution est engendré par la rotation d’un triangle rectangle autour de l’un des côtés de l’angle droit.
V) Section plane d’un solide :
	Dessiner la section du cube (ABCDA’B’C’D’) par le plan (MNP)
	Les droites (PN) et (DC) appartenant au plan ( DCC’) se coupent en alpha. Les droites 5NM) et (BC) appartenant au plan (CBB’) se coupent en bêta . La droite (alpha , bêta)est la droite d’intersection du plan (ABC) et du plan (MNP). Le point gamma est le point d’intersection des droites ( alpha- bêta) et (AB) La droite ( gamma- M) appartient au plan ( MNP) et elle coupe la droite (A’B’) en Q. La section plane est donc le quadrilatère (MNPQ). Remarque : selon la position des points M , N, et P , la section plane du cube peut être un triangle , un quadrilatère , un pentagone ou un hexagone. ‘

Leçon	LA GEOMETRIE DANS LE PLAN ET DANS L’ESPACE.
N°	TRAVAUX d ’ AUTO - FORMATION sur S

TRAVAUX N° d ’ AUTO - FORMATION : CONTROLE

TRAVAUX N° d ‘ AUTO - FORMATION EVALUATION

	Considérons la pyramide ABCD, pyramide régulière à base triangulaire.	Appelée : polyèdre régulier portant le nom de tétraèdre.
	Chacune des faces est un triangle (nature) : ……………
	Chacune des faces est une partie d’un plan. Cette pyramide est posée sur un plan horizontal ( P)
	Le sommet A appartient - il au plan (P) ?
	Les points B, C et D appartiennent -il au plan (P) ?
	Tracer sur la figure la droite (d) passant par les points B et C. Le plan (P) peut aussi être déterminé par la droite (d) et le point D. Tracer la droite (d’) passant par les points C et D. Quelle est l’intersection des droites ( d) et ( d’) ? (d) Ç (d’) = …….. Le plan peut aussi être déterminé par les deux droites (d) et ( d’).
	Exercice 1 : Par quels éléments peut être déterminé le plan de la face ABC ?	Par la droite (d) et le point A Par les points ABC. Par un point et une droite : Par la droite (BC) et le point A Par la droite passant par (AB) et le point C Par la droite ( AC) et le point B Par les deux droites : (AB) et (BC) ; ou ( BA) et AC) ou par (BC) et (AC)
	Même question pour le plan de la face ABD
	Quel est le plan déterminé par le point A et la droite ( d’) ?
	Répondre par « vrai » ou « faux »
	Le point « C » appartient au plan ( ABD) :……	faux
	La droite (AC) et le point « D » déterminent le même plan que la droite (AC) et le point « B » :	faux
	La droite (CD) et le point « b » déterminent le même plan que la droite (BC) et le point « D » :	…vrai
B) Considérons un parallélépipède rectangle (ABCDFGHE).
	Chacune de ses faces correspond à un plan. Chacune de ses arêtes correspond à une droite. On peut s’aider du développement (ou patron) du parallélépipède . (ici modèle)
	1°)Positions relatives droite et plan.
	Considérons la droite (FH) et le plan (FEH).Tous les points appartiennent au plan la droite (FH) est « contenue » dans le plan (FEH)
	Considérons la droite (FC) et le plan (FEH). Le plan et la droite ont un seul point commun, le point « F » Le point « F » est l’intersection de la droite (FC) et du plan (FEH) La droite (FC) est « sécante » au plan (FEH) au point « F »
	Considérons la droite (BD) et le plan (FEH) . La droite et le plan n’ont aucun point commun. La droite (BD) est « parallèle » au plan (FEH)
	2°) Positions relatives de deux droites : (voir le parallélépipède (ABCDEFGH) )
	►La droite ( AB) est contenue dans le plan ( ABG)
	La droite ( AF) est contenue dans le plan ( ABG)
	Les droites ( AB) et ( AF) , contenues dans un même plan sont « coplanaires ».
	►Les droites (AB) et (AF) sont contenues dans un même plan et ont un point commun. Les droites ( AB) et (AF) sont « coplanaires » et « sécantes ».
	►Les droites ( AB ) et (FG) sont contenues dans le plan (ABG). Elles sont parallèles. Les droites (AB) et ( FG) sont « coplanaires » et « parallèles ».
	►Il n’existe pas de plan contenant à la fois les droites (FC) et (AB). Les droites 5FC) et (AB) sont « non coplanaires ».
	3°) Positions relatives de deux plans distincts.
	►Dans le tétraèdre : Quelle est la partie commune aux plans ( BAC) et (P) ?	Le point A
	L’intersection des plans ( BCA) et (P) est la droite (BC) les plans (P) et ( BAC) sont sécants.
	►Dans le parallélogramme ( ABCDEFGH) les plans ( EFAD) et ( HGBC) n’ont aucune partie commune. Les plans ( EFAD) et (HGBC) sont parallèles.
	Exercice 2 :
	le tétraèdre. (répondre par « vrai » ou « faux »
	La droite (AC) appartient au plan (ABC) …………..	v
	La droite (AC) appartient au plan (BCD)	f
	Le parallélogramme :
	La droite (CG) est parallèle au plan (FED)	f
	La droite (AB) est contenue dans le plan ( AFG)	f
	La droite (GH) est sécante au plan (BCH)	v
	Citer une droite contenue dans le plan (DCH)	(AB)
	Citer une droite sécante (mais non perpendiculaire) au plan (ABC)	(FB)
	Citer une droite perpendiculaire au plan ( ABC)	(BG)

Exercice 3 : A partir du parallélogramme (ABCDEFGH)

A) Compléter le tableau suivant Lmettre une croix dans la case qui convient.

	Non coplanaires		Coplanaires
	Non orthogonales	orthogonales	Parallèles	Sécantes non perpendiculaires	Sécantes perpendiculaires
( BC) et ( BG)
( FG) et ( HC)
( AH) et ( AB)
( EF) et ( AD)
( ED) et ( DH)
( AB) et ( EC)
( GH) et ( AD)
( FH) et ( DB)

B)

Citer deux plans parallèles………………………

Citer deux plans sécants et non perpendiculaires :………………………

Citer deux plans perpendiculaires :……………………………………….

Quelle est la position relative des plans ( ADHG) et ( EFBC) : ……………….

Exercice 4 :

Exercice 4 :

Traduire par une figure la situation suivante : Deux droites (d) et (D) appartiennent au plan (P), elles sont sécantes en « M ». La droite « δ » est perpendiculaire à (P) et passe par « M ».

Exercice 5 :

Traduire par une figure la situation suivante : soit une droite (D) et un plan (P) de l’espace « A » et « B » sont deux points distincts de (D). La droite (D) coupe le plan (P) en un point « M » situé entre « A » et « B».

Exercice 6:	Observer le solide de la figure ci contre :
Les faces ABCD et A’B’C’D’ sont parallèles. Les faces latérales sont des trapèzes isocèles et les bases ABCD et A’B’C’D’ sont des carrés. A) Citer deux droites parallèles :………………………….. B) Deux droites sécantes :……………………………….. C) Deux droites non coplanaires : ……………………….. D) Citer deux plans sécants : …………………………….. ; préciser leur intersection :…………….