Pré requis:

Lecture : géométrie descriptive

Lecture : La représentation en Perspective

A consulter : Les volumes particuliers.

ENVIRONNEMENT du dossier:

Index accueil warmaths

AVANT : 1°)Notion 2°) A voir !!! 3°) leçon qui était faite au collège « étude descriptive de l’espace » )!!!(avant 2013)

COURS

APRES : 1°) L’orthogonalité 2°) le parallélisme.

Info : Liste des cours sur la géométrie dans l’espace. 2. Cours :niveau IV Cours

TITRE : Plan et droite dans l ‘espace .

1°)DEFINITION et AXIOMES

2°)DETERMINATION D’UN PLAN

3°)REGIONNEMENT DE L’ESPACE

4°) POSITIONS RELATIVES DE DEUX PLANS

5°) POSITIONS RELATIVES D’UNE DROITE ET D’UN PLAN.

6°) POSITION RELATIVES DE DEUX DROITES DE L’ESPACE

7°) TETRAEDRE ( tétraèdre) 

			Exercice série 1
Travaux ; devoirs			Exercices série 2	Corrigé
TEST	Contrôle	évaluation		Contrôle	évaluation

Interdisciplinarités : (matière concernée)
F	H	Géo.	Vie quotidienne et vie familiale	Autres :	Sciences et technique	Physique Chimie Electricité	Statistique.

COURS

1°) DEFINITION et AXIOMES

L’espace est un ensemble noté « E » dont les éléments sont  appelés « points »

Les droites et les plans sont des parties propres de l’ensemble « E » .

Les relations sont décrites par les axiomes suivants :

Axiome 1 : il existe une droite est une seule contenant deux points distincts « A » et « B » de l’espace .

On dira que la droite passe par A et B , on dit aussi que les points A et B déterminent la droite . On note cette droite ( A B ) .

Axiome 2 : Toute droite dont deux points distincts appartiennent à un plan est incluse dans ce plan .

( Rappel Info sur la position d’une droite par rapport à un point )

Axiome 3 : Il existe un plan et un seul plan contenant trois points distincts non alignés .

( Rappel Info : détermination d’un plan)

On convient de déterminer un plan par un parallélogramme. Analogie avec l’image d’une face d’une planche à dessin ou de la surface horizontale d’une table .

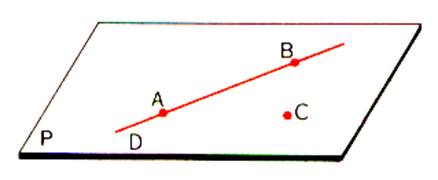
La représentation graphique ci –contre permet d’illustrer les axiomes 2 et 3 .

2°) DETERMINATION D’UN PLAN .

Il en résulte des axiomes précédents , qu’un plan est déterminé :

a°) si A , B et C sont les trois points , le plan sera désigné par :

plan ( ABC)

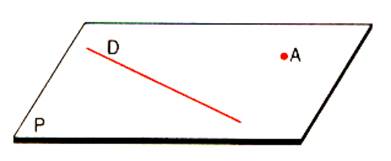
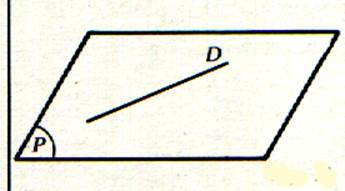
b°)par une droite et un point n’appartenant pas à cette droite .

Sur la droite il suffit de choisir deux points distincts quelconques. Ce qui se ramène au cas précédent . Le plan P défini par la droite D et le point « A »et est désigné par : plan ( A , D ).

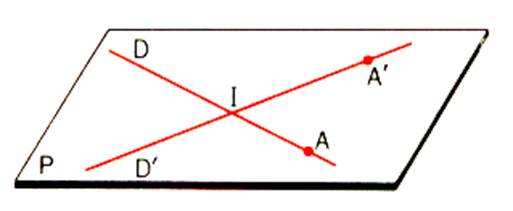
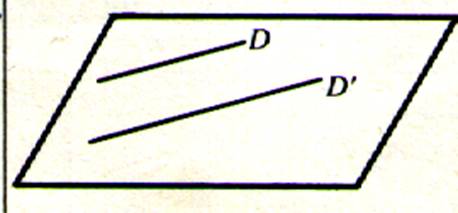
c°) Par deux droites concourantes .

Soit I le point d’intersection des droites D et D’ . Nous considérons le point A distinct de I appartenant à D , et le point A’ distinct de I , appartenant à D’ . Le plan défini par les trois points A , I , A’ contient les droites D et D’ . Ce plan est noté ( D et D’ ) .

3°) REGIONNEMENT DE L’ESPACE .

Observons la surface supérieure d’une table horizontale ,partie d’un plan , nous distinguons les points dans l’espace qui sont au dessus de la table et les points qui sont au -dessous de la table . Cette observation nous conduit aux axiomes suivants :

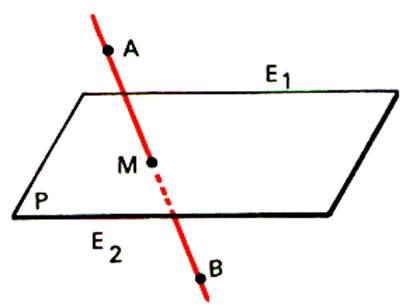
Axiome 4 : Un plan partage l’espace « E » en deux demi – espaces E₁ et E₂ non vides et disjoints .

Axiome 5 : Si A et B sont deux points appartenant respectivement à E₁ et E₂ , l’intersection du plan et de la droite passant par A et B est un point et un seul.

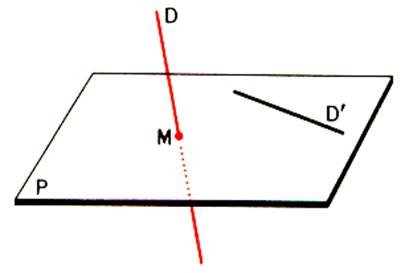
La droite ( A B ) joignant A de E1 et un point B de E2 admet un point commun et un seul « M » avec le plan P

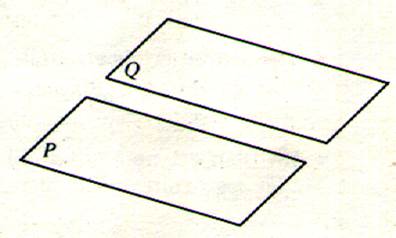
4°) POSITIONS RELATIVES DE DEUX PLANS. ( info plus !)

Soit deux plans donnés ; P et Q .

Par convention de représentation on dira que : Ces deux plans sont parallèles.

a) « P » et « Q » ont trois points communs non alignés .

Tout point de l’un appartient à l’autre . On dit que les deux plans sont « confondus » ou « égaux » .On écrit : P = Q

b) « P » et « Q » sont distincts et ont en commun deux points distincts A et B .

d’après l’axiome 2 , la droite ( A B ) est incluse dans P et incluse dans Q . Les deux plans n’ont pas d’autre point commun en dehors de la droite (AB) , sinon ils seraient confondus .

On dit que P et Q sont sécants , leur droite commune est D , elle est leur droite d' intersection. Les plans peuvent être perpendiculaires. Pour cela il faut qu’un plan possède une droite orthogonale à l’autre plan.

Application : pour démontrer que trois points de l’espace sont alignés , il suffit de démontrer qu’ils sont communs à deux plans distincts .

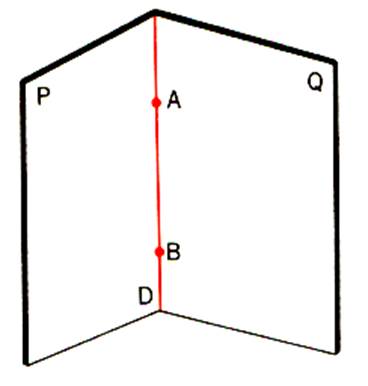
c) « P » et « Q » sont distincts et ont un point commun A .

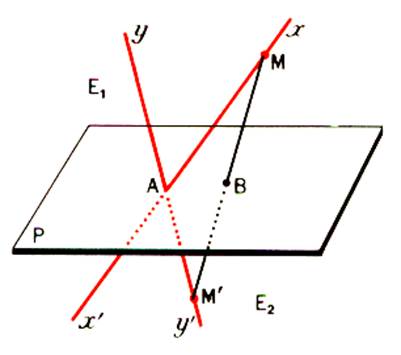
Soit E1 et E2 les demi – espaces définis par P et soit dans Q deux droites x’A x et y’A y . Si l’une d’elles appartient à P , c’est l’intersection de P et Q . Sinon les demi – droites [ A x ) et [ A y ) sont par exemple dans E1 , [ A x’ ) et [ A y’ ) dans E2 Soit M un point de [ A x ) et M’ un point de [ A y’ ) . La droite ( M M’) coupe le plan P au point B distinct de A . Les plans P et Q ont donc pour intersection la droite ( A B ) .

Donc :

Si deux plans distincts ont un point commun , leur intersection est une droite contenant ce point .

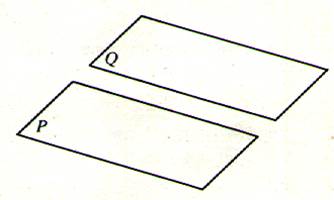
d) P et Q n’ont aucun point commun.

Deux plans qui n’ont aucun point commun sont dit « parallèles » .

5°) POSITIONS RELATIVES D’UNE DROITE ET D’UN PLAN. (info plus ! !)

Soit une droite « D » et un plan « P »

a) « D » contient deux points appartenant à « P »

Si « D » contient deux points appartenant à « P » alors : la droite « D » est incluse dans « P » . ( axiome 2)

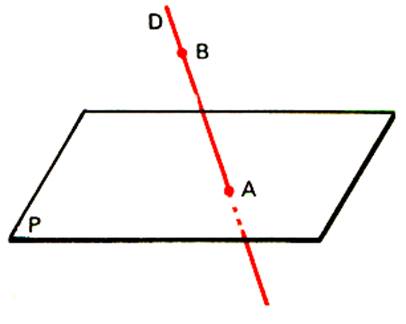
b) Si « D » contient un point « A » appartenant à « P » et un point « B » n’appartenant pas à « P » .

Alors : La droite D n’est pas incluse dans « P » ; on dit que la droite « D » est « sécante » au plan « P » ou qu ‘elle coupe le plan « P ».

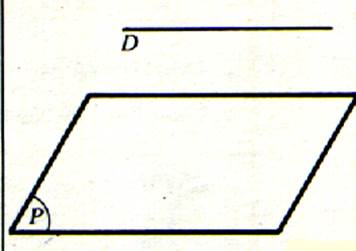
c) Si « D » et « P » n’ont aucun point commun .

Alors la droite et le plan sont alors « parallèles ».

.( Info plus ! !)

6°)POSITION RELATIVES DE DEUX DROITES DE L’ESPACE.

Soit deux droites « D » et « D’ » de l’espace E , on rencontrera 3 cas !

a) Si « D » et « D’ » ont un point commun .

Elles sont « concourantes » et elles déterminent un plan ; elles dites « coplanaires » .

b) Si « D » et « D’ » ont tous leurs points , en commun .

Les droites « D » et « D’ » sont « confondues »  et elles déterminent un plan ; elles dites « coplanaires » .

c) Si « D » et « D’ » n’ ont pas de point commun.

Soit « M » un point de « D » et « P » le plan défini par « M » et « D’ » .

c1) Si la droite « D » est incluse dans le plan « P » , alors dans ce plan , « D » et « D’ » sont parallèles.

c2) Si « D » n’est pas incluse dans le plan « P » , alors les deux droites « D » et « D’ » sont dites quelconques et « non coplanaire »  .

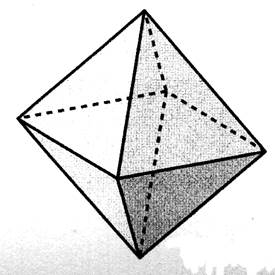
7°) TETRAEDRE ( tétraèdre) : (info plus ! ! !)

On appelle « tétraèdre » un ensemble de quatre points non coplanaires.

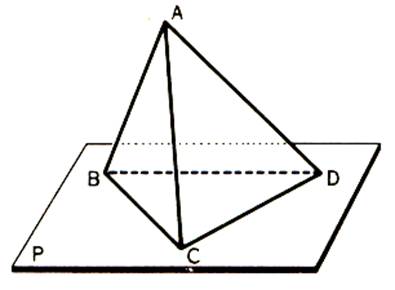
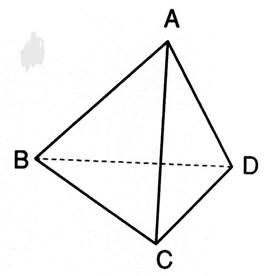
Les points A,B,C,D sont les « sommets » du tétraèdre ; ils déterminent six segments [AB] , [AC] , [AD], [BC], [BD], [CD] qui sont les arêtes du tétraèdre. Deux arêtes non concourantes telles que [AB] [CD] sont dites « opposées ».

Exemples :

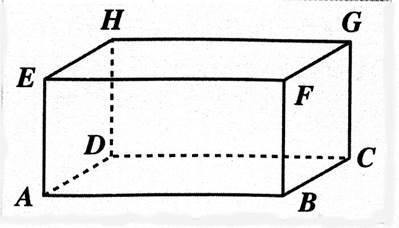
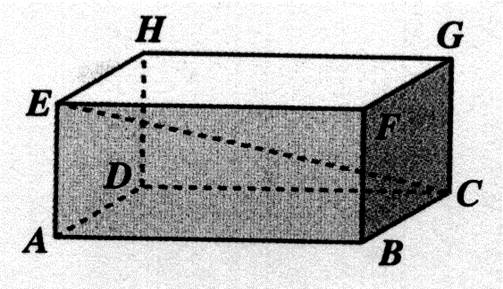
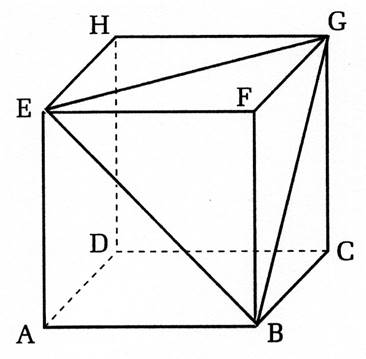
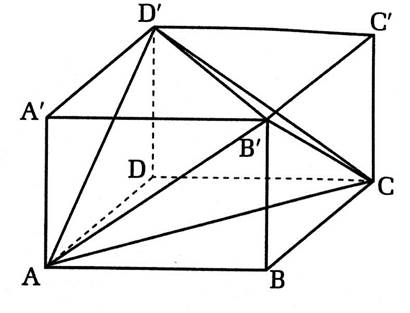
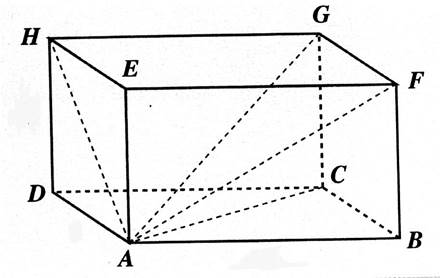
	Si on considère le parallélépipède ABCDEFGH ; Les droites ( AE ) et ( BC) sont orthogonales. La droite (EA) est orthogonale au plan ( ABCD) La droite (FE) est parallèle au plan ( ABCD) Les plans ( ADHE) et ( BCGF) sont parallèles . Les plans ( ADHE) et ( ABCD) sont perpendiculaires.
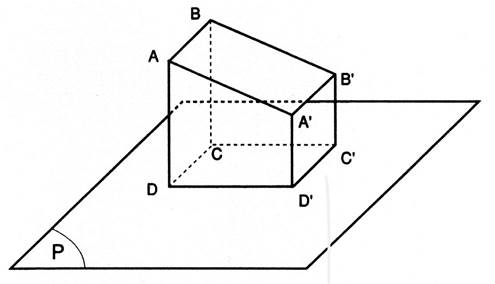
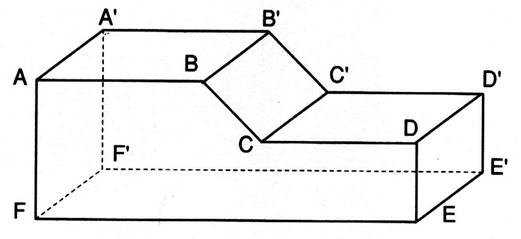
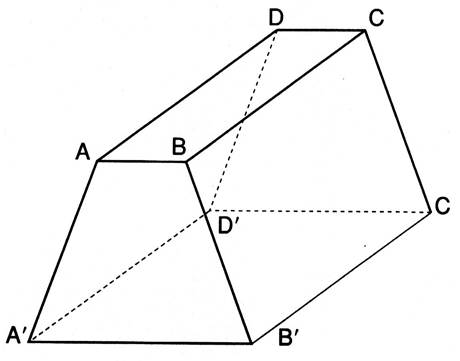
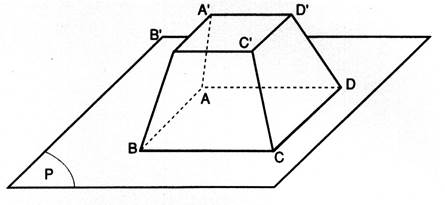
	On considère le prisme AB B’A’ DC C’ D’ Le plan AB B’A’ n’est pas parallèle au plan DC C’ D’ .
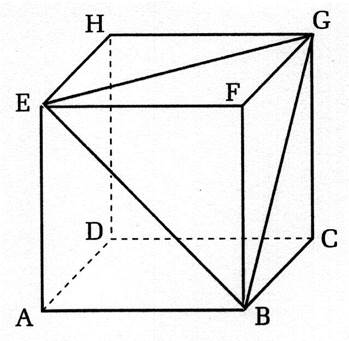
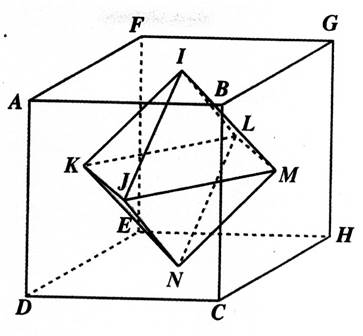
	La droite (EC) est la diagonale du plan EGCA .

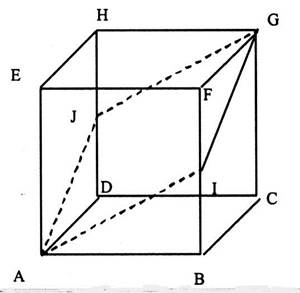
TRAVAUX AUTO FORMATIFS.

CONTROLE:

EVALUATION:

Discuter sur la position des droites  :