La trigonométrie _ sommaire

 

 

 

 

 

 

Liste des cours sur la :TRIGONOMETRIE :

 

 

 

 

PRE  REQUIS:

 

 

Liste des connaissances pré requises (important)prerequistrigo.htm

 

 

 

 

 

 

VOCABULAIRE : « noms » donnés aux cotés  du triangle rectangle , pour aborder la trigonométrie.

 

 

Environnement du dossier :

Index warmaths

Les triangles rectangles: résolution   Sphère metallique

Objectif suivant Sphère metalliquele cercle trigonométrique

1°) Liste des cours sur la trigonométrie   pour   formation VI et V      Sphère metallique

 

2°)INFO : table des matières  pour toutes formations

 

3°)  MODULE : LE CERCLE TRIGONOMETRIQUE.

 

 

Commentaire :

Cette partie de la trigonométrie est centrée  sur  l’étude  des relations trigonométriques dans le triangle rectangle .

Une seconde partie traitera des relations trigonométriques dans le triangle quelconque.

Il est important de revoir les « pré requis » pour aborder sereinement ces études.

 

PARTIE 1 :   LA  TRIGONOMETRIE ET LES LIGNES TRIGONOMETRIQUES.

 

 

 

1.                         Notions de trigonométrie

 

 

 

2.                         Les lignes trigonométriques d’un angle aigu.

 

 

 

3.                         Propriétés des lignes trigonométriques.

 

 

 

4.                       Ligne trigonométriques d’un angle obtus , remarquable et quelconque .

 

 

 

5.                         Rapports trigonométriques :  « sécante » et « cosécante ».

 

 

 

6.                       VOCABULAIRE utilisé pour le triangle rectangle:

Boule verte

 

 

7.                       Travaux préparatoires

Boule verte

 

 

8.                      Construire un angle .

Boule verte

 

 

9.                      Relations trigonométriques dans les Triangles :  Rectangles et quelconques.

 

 

 

10.            Relations trigonométriques  dans le triangle quelconque. (règle des sinus)

 

 

 

Nota : Après avoir mis en évidence l’existence des lignes trigonométriques , l’exploitation de ces connaissances passe par ce que l’on appelle : les rapports trigonométriques.

 

 

 

 

               PARTIE 2 :    LES RAPPORTS TRIGONOMETRIQUES

 

 

Leçon : les rapports trigonométriques.

 

11.            Usage des tables :La table  de trigonométrie et   son exploitation

 

 

 

12.            Objectif   :     SINUS

 

 

 

13.            Objectif       COSINUS

 

 

 

          Voir fiches : 4ème collège : « cosinus » et « projection orthogonale »

 

 

 

Voir fiches 3ème : n°1   

 

 

 

Voir fiches 3ème n°2

 

 

 

14.            Objectif :  TANGENTE  et cotangente …

 

 

 

15.            Objectif  : tangente en un point d’une courbe  

 

 

 

16.            Cosinus et sinus d’un réel

 

 

Applications : tracé et mesure d’angle dont on connaît les rapports trigonométriques

 

 

 

PARTIE 3 :  LES  COURS ET TRAVAUX

 

 

 
  1. TESTS  ou DEVOIR ….

 

 

 
  1.  Situations problèmes utilisant les rapports trigonométriques.

 

 

 
  1. «Exemples de   10  situations  problèmes sur l’application des relations trigonométriques.

 

 

 
  1. Contrôle et évaluation niv V sur les triangles rectangles.

 

 

 
  1. Contrôle et évaluation niv V : sur les triangles quelconques .

 

 

 
  1. Recherche de la longueur du troisième côté ,lorsque l’on connaît deux longueurs et l’ angle formé par ces deux côtés. :Avec la relation : « a2 = b2  +  c2 - 2bc cos  »

 

 

 
  1. SITUATIONS PROBLEMES :  DESSIN et ATELIER mécanique .

 

 

 
  1. Situations problèmes : levée de plan et ARPENTAGE.

 

 

 
  1. CC sinus

 

 

 

 

 

MODULE : >>aller vers     les cours et leçons sur >>>>>     LE CERCLE TRIGONOMETRIQUE.

 

 

 

 

Cours les plus utilisés :

 

1.  Classe  niveau V  « CAP » dans le T.R.     -  Devoir exercices types - 

 

2.  Classe BEP : relations métriques

 

3.  Cos d’un réel

 

4.  Le cercle trigonométrique

 

5.  Tangente d’un réel

 

6.  Les sinusoïdes et les cosinusoides

 

7.  Variation des nombres trigonométriques  

 

 

Ci –dessous :  Objectifs de formation particuliers :

 

 

 

 

 

1. >>Les relations trigonométriques dans le triangle rectangle

 

 

 

 

> 

2. >>Les relations trigonométriques dans le cercle trigonométrique

 

 

 

 

 

3. LE CERCLE TRIGONOMETRIQUE.

 

 

 

4. LES FONCTIONS TRIGONOMETRIQUES.(circulaires)

 

 

 

5. L’intégrale trigonométrique.

 

 

 

 

 

 

 

 

Exemple de PB :

 

 

 

 

 

 

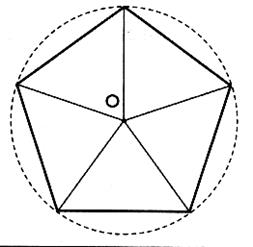
On considère un pentagone  régulier inscrit dans un cercle de rayon 6 cm .

 a)Quelle est la nature  de chacun de ces cinq triangles dont le sommet  est le centre  "O" du cercle .

b)Donner une mesure de chacun de leurs angles . ( rappel :la somme des angles d'un triangle est de 180 ° )  . 

c)Calculer l'aire de ce pentagone . ( pour calculer  "h"  la trigonométrie) .

 

 le  corrigé  est à la page suivante  :

 

 

 

penta

 

 

 

 

 

 

Corrigé : On considère un pentagone  régulier inscrit dans un cercle de rayon 6 cm .

 a)Quelle est la nature  de chacun de ces cinq triangles dont le sommet  est le centre  "O" du cercle .  le triangle est un triangle isocèle  .(  360 ° / 5 =  72° )

b)Donner une mesure de chacun de leurs angles . ( rappel :la somme des angles d'un triangle est de 180 ° )  .  si l’angle au sommet 72° ; la somme des deux autres angles = 180 - 72° = 108 ° ; un angle de base =  108° :2 = 54°

c)Calculer l'aire de ce pentagone . ( pour calculer  "h"  la trigonométrie) .

Aire d’un triangle : il faut savoir calculer la hauteur « h » , distance qui va du centre à la base ? ( voir la trigonométrie )

Hypoténuse = 6 cm ; hauteur : sinus 54°  = 0,809  = h / 6 ; donc   h = 6 fois 0,809 = 4,85 cm ; base : cos 54° = 0,588  = b / 6  = 6 fois 0,588 = 3,53)

Un demi triangle : ( 4,85 fois  3,53  ) / 2 =  17,12 cm² ; il y a 10  demi - triangles équilatéral ; l’aire du pentagone =  17,12 fois 10 = 171,2 cm²

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Arial'>